Х.15. Расчет деформаций балки

При использовании упрощенного метода расчета, прогибы предварительно напряженных конструкций допускается рассчитывать, исходя из принципа суперпозиции, т.е. суммируя прогибы от внешних нагрузок и предварительного обжатия

,

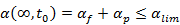где α_f – прогиб от внешних нагрузок;

𝛼_p – прогиб от предварительного обжатия (выгиб).

Максимальный прогиб в середине пролета двускатной балки покрытия может быть определен по формуле:

,

где – мгновенный прогиб от полной нагрузки;

– прогиб (мгновенный) от практически постоянного сочетания нагрузок;

– остаточный (длительно действующий) прогиб от практически постоянного сочетания нагрузок.

Мгновенный прогиб α_0,k+d от полной нагрузки, мгновенный прогиб 𝛼_0,d от практически постоянного сочетания нагрузок и прогиб 𝛼_p от предварительного обжатия (выгиб) определяются для элементов с трещинами по формуле

(15.1)

где – эффективный модуль упругости бетона;

, – соответственно момент инерции сечения с трещиной и без трещины, определяемый с учетом отношения ;

Значения эффективного модуля упругости бетона E_c,eff определяются:

– при действии кратковременной нагрузки

E_c,eff = E_cm;

– при действии длительной нагрузки

_,

где Ф(∞,t₀) – предельное значение коэффициента ползучести для бетона.

M_Sd,n – изгибающий момент от соответствующего сочетания нагрузок или вызванный усилием обжатия.

M_cr – изгибающий момент, при котором образуются трещины.

Для железобетонных элементов без трещин жесткость сечения определяют по формуде (15.1) принимая I_II = I_I.

Формулы для расчета моментов инерции сечения для железобетонных элементов, имеющих полку в сжатой зоне, приведены в таблице методички.

Прогиб при мгновенном действии полной нагрузки.

Изгибающий момент в расчетном сечении при действии полной нагрузки равен

M_i = 1758,8 кНм.

.

Вычисляем момент инерции сечения без трещины I_I

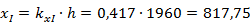мм

мм⁴

Вычисляем момент инерции сечения с трещиной I_li

=

мм⁴

кНм

Определяем жесткости сечения при мгновенном действии полной нагрузки

нмм² кНм²

Определяем мгновенный прогиб 𝛼_0,k+d от полной нагрузки по формуле

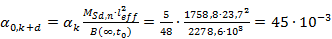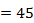м мм

Прогиб при мгновенном действии практически постоянного сочетания нагрузок

Далее определяем жесткости сечения при мгновенном действии практически постоянной нагрузки.

Момент от этой нагрузки равен кНм

нмм² кНм²

Определяем прогиб 𝛼_0,k при мгновенном действиипрактически постоянного сочетания нагрузок по формуле

м мм

Прогиб при длительном действии постоянного сочетания нагрузок

Определяем эффективный модуль деформаций

МПа,

.

Вычисляем момент инерции сечения без трещины I_I

мм

мм⁴

Вычисляем момент инерции сечения с трещиной I_li

=

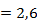
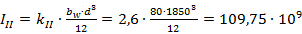мм⁴

Определяем жесткости сечения при длительном действии практически постоянного сочетания нагрузок

нмм² кНм²

Определяем мгновенный прогиб 𝛼_∞,d при длительном сочетании практически постоянного сочетания нагрузок

м мм

Тогда прогиб в середине пролета двускатной балки покрытия от внешних нагрузок равен

мм.

Прогиб середины балки от предварительного обжатия (выгиб)

Прогиб середины балки от предварительного обжатия (выгиб) определяется как

.

Принимаемое при расчете усилие обжатия влияет благоприятно и поэтому принимается по сниженному значению усилия обжатия (после проявления всех потерь)

кН.

Жесткость сечения принимается лдя сечения без трещин при условии учета длительности действия нагрузки.

Тогда нмм² =

кНм².

Прогиб середины балки от предварительного обжатия (выгиб) равен

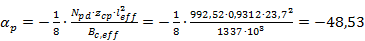мм.

Полный прогиб середины балки

Полный прогиб середины балки от внешних нагрузок и предварительного обжатия равен

мм мм

4. Расчёт внецентренно нагруженного фундамента.

Дата добавления: 2015-10-13