Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Расчет погрешностей прямых измерений.

Читайте также:
  1. II. В случае наличия в городе (регионе) прямых чартерных рейсов до страны пребывания за границей и обратно.
  2. II. Заполненные таблицы. Расчетные формулы и расчеты.
  3. III. Расчетные формулы и пояснения к ним. Сравнение результатов расчета и эксперимента.
  4. V2: Расчет издержек производства.
  5. А) Определение расчетных усилий в ветвях колонны
  6. А. Расчет производительности местных отсосов.
  7. Автомобильные дороги в зависимости от расчетной интенсивности движения и их хозяйственного и административного значения подразделяются на I-а, I-б, I-в, II, III, IV и V категории.

 

5.1 Определяем стандартную погрешность измерения угла отскока шарика.

Формула:

 

S I = (S/ I)2 + (S// 2)2.

 

S I - среднеквадратичное отклонение.

S/ I - стандартная случайная погрешность.

S// 2 = 0, 5 - стандартная систематическая погрешность.

 

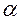S/ I = ∑( I - < 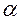i>)2 / N (N - 1)

N=10 количество измерений угла.

 

S/ 1= (180-17.50)2+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(18.50-17.50)2+(170-17.50 )2

+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(180-17.50)2 / 10(10-1) = 0,176;

S = (0, 5)2+(0,176)2 = 0,530;

 

S/ 2= (270-26.50)2+(27.50+26.50)2+(260-26.50)2+(26.50-26.50)2+(270-26.50)2+(270-26.50)2+(26.50-26.50)2+(270-26.50)2+(26.50-26.50)2+(26.50-26.50)2 / 10(10-1) = 0,148;

S = (0, 5)2+(0,148)2 = 0,521;

 

S/ 3= (350-35.50)2+(35.50-35.50)2+(35.50-35.50)2+(360-35.50)2+(35.50-35.50)2+(35.50-35.50)2+(350-35.50)2+ (350-35.50)2+(350-35.50)2+(35.50-35.50)2 / 10(10-1) = 0,104

S = (0, 5)2+(0,104)2 = 0,510;

 

S/ 4= (43-43)2+(43-43)2+(43.5-43)2+(42-43)2+ (43-43)2+(43.5-43)2+(42.5-43)2+ (43-43)+ (43-43)2 +(42.5-43) / 10(10-1) = 0,139

S = (0, 5)2+(0,139)2 = 0,518;

 

S/ 5= (500-500)2+(500.5-500)2+ (500-500)2+(50.50-500)2+ (50.50-500)2+ (50.50-500)2+ (510-500)2+ (500-500)2+(49.50-500)2+ (50.50-500)2 / 10(10-1) = 0,158;

S = (0, 5)2+(0,158)2 = 0,524

 

5.2 Расчет абсолютной погрешности угла отклонения шарика ∆ i

 

Формула:

 

∆ i = (kn * S/ i)2+(1/3*k*S// 2 )2

 

kn = 2.3 - соответствующий коэффициент Стьюдента;

k = 2.0 - соответствующий коэффициент Стьюдента;

 

Производим вычисления:

 

∆ 1 = (2.3*0,176)2+ (1/3*2.0*0, 5)2= 0,524

 

∆ 2 = (2.3*0,148)2+ (1/3*2.0*0, 5)2= 0,476

 

∆ 3 = (2.3*0,104)2+ (1/3*2.0*0, 5)2= 0,410

 

∆ 4 = (2.3*0,139)2+ (1/3*2.0*0, 5)2= 0,461

 

∆ 5 = (2.3*0,158)2+ (1/3*2.0*0, 5)2= 0,493

5.2 Определяем относительную погрешность измерения угла отскока шарика.

Формула:

 

ε i = ∆ I / < i>

 

ε 1 = 0,524 / 17,50 = 0,029;

 

ε 2 = 0,476 / 26,50 = 0,016;

 

ε 3 = 0,410 / 35,50 = 0,012;

 

ε 4 = 0,461 / 43,00 = 0,011;

 

ε 5 = 0,493 / 50,00 = 0,010;

 

5.3 Определяем относительную и абсолютную погрешность измерения угла отклонения шарика.

 

Формулы:

 

∆ i = (kn * S/ i)2+(1/3*k*S// 2 )2

ε i = ∆ I / < i>

 

т.к. (kn * S/ i)2 = 0, то ∆ i = (1/3*k*S// 2 )2.

 

Производим вычисления:

 

∆ I = (1/3*2.0*0.5)2 = 0,33

 

 

ε 1 = 0,33/20 = 0,016;

 

ε 2 = 0,33/30 = 0,011;

 

ε 3 = 0,33/40 = 0,008;

 

ε 4 = 0,33/50 = 0,007;

 

ε 5 = 0,33/60 = 0,006;

 

 

5.4 Рассчитаем относительную погрешность измерения времени соударения шарика.

Формула:

S 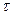I = ∑( i- < i>)2 / N (N - 1)

 

Производим вычисления:

S 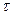1= (321-309)2+(312-309)2+(304-309)2+(312-309)2+(303-309)2+(307-309)2+(315-309)2+(309-309)2+(302-309)2+(311+309)2 / 10(10-1) =1,8*10-7

 

S 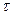2= (272-287)2+(288-287)2+(271-287)2+(297-287)2+(287-287)2+(301-279)2+(286-287)2 +(291-287)2+(300-287)2 +(279-287)2 / 10(10-1) =3,37*10-7

 

S 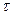3= (262-269)2+(267-269)2+(269-269)2+(262-269)2+(258-269)2+(252-269)2+(261-269)2 +(243-269)2+(255-269)2+ (261-269)2 / 10(10-1) = 4,10*10-7

 

 

S 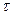4= (217+217)2+(216-217)2+(208-217)2+(212-217)2+(206-217)2+(231-217)2+(214-217)2+ (227-217)2+(221-217)2+(211-217)2 / 10(10-1) = 2,71*10-7

 

S 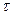5= (191-191)2+(189-191)2+(192-191)2+(184-191)2+(190-191)2+(183-191)2+(202-191)2+ (193-191)2+(201-191)2+(186-191)2 / 10(10-1) = 2,27*10-7

 

5.5 Определим абсолютную погрешность измерения времени соударения шарика.

 

Формула:

∆ I = (kn*S 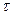)2+(1/3*k* S/ 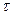)2

S 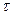- стандартная случайная погрешность.

S/ 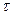=0,01 - стандартная систематическая погрешность.

 

 

Производим вычисления:

∆ 1 = 10-7* (2,3*1,8)2+(1/3*2,0*0,01)2 = 4,14*10-7;

 

∆ 2 = 10-7* (2,3*3,37)2+(1/3*2,0*0,01)2 = 7,75*10-7;

 

∆ 3 = 10-7* (2,3*4,10)2+(1/3*2,0*0,01)2 = 9,43*10-7;

 

∆ 4 = 10-7* (2,3*2,71)2+(1/3*2,0*0,01)2 = 6,23*10-7;

 

∆ 5 = 10-7* (2,3*2,27)2+(1/3*2,0*0,01)2 = 2,28*10-7;

 

5.6 Определим относительную погрешность измерения времени соударения шарика.

Формула:

ε 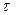= ∆ I / < i>

 

ε 1= 4, 14*10-7 / 309 * 10-7 = 0,013;

 

ε 2= 7, 75*10-7 / 287* 10-7 = 0,027;

 

ε 3= 9, 43*10-7 / 269 *10-7 = 0,035;

 

ε 4= 6, 23*10-7 / 217* 10-7 = 0,028;

 

ε 5= 2, 28*10-7 / 191* 10-7 = 0,012;

 

 

Дата добавления: 2015-10-13; просмотров: 70 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Расчет скорости шарика до и после удара.| Расчет погрешностей теоретически полученных результатов
mybiblioteka.su - 2015-2024 год. (0.018 сек.)