
Читайте также:
|
6.1. Рассчитаем погрешность измерения скорости до удара
Формулы:
ε  I = ½*
I = ½*  εg+ε2L+(ctg(
εg+ε2L+(ctg(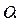 i/2)*∆
i/2)*∆ 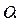 )2
)2
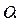 I – Угол отклонения шарика.
I – Угол отклонения шарика.
∆ 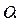 - Абсолютная погрешность измерения угла отклонения в радианах.
- Абсолютная погрешность измерения угла отклонения в радианах.
∆ 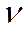 I = ε
I = ε  I /
I / 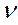 I
I
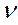 I - скорость шарика до удара.
I - скорость шарика до удара.
Производим вычисления:
ε  I = ½*
I = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(200/2)*0,005)2= 0,015;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(200/2)*0,005)2= 0,015;
ε  2 = ½*
2 = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(300/2)*0,005)2= 0,005;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(300/2)*0,005)2= 0,005;
ε  3 = ½*
3 = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(400/2)*0,005)2= 0,005;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(400/2)*0,005)2= 0,005;
ε  4 = ½*
4 = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(500/2)*0,005)2= 0,005;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(500/2)*0,005)2= 0,005;
ε  5 = ½*
5 = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(600/2)*0,005)2= 0,006;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(600/2)*0,005)2= 0,006;
∆ 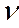 1= 0,015 / 0,605 = 0,024 (м/c);
1= 0,015 / 0,605 = 0,024 (м/c);
∆ 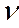 2= 0,005 / 0,905 = 0,006 (м/c);
2= 0,005 / 0,905 = 0,006 (м/c);
∆ 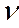 3= 0,005 / 1,197 = 0,004 (м/c);
3= 0,005 / 1,197 = 0,004 (м/c);
∆ 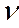 4= 0,005 / 1,479 = 0,003 (м/c);
4= 0,005 / 1,479 = 0,003 (м/c);
∆ 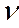 5= 0,006 / 1,757 = 0,003 (м/c);
5= 0,006 / 1,757 = 0,003 (м/c);
6.2 Определим погрешность расчета скорости шарика после удара.
Формулы:
ε  I = ½*
I = ½*  εg+ε2L+(ctg(<
εg+ε2L+(ctg(< 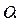 i>/2)* ∆<
i>/2)* ∆< 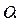 i>)2
i>)2
∆< 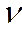 I >= ε<
I >= ε<  I> /
I> / 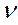 I
I
∆< 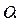 i> - абсолютная погрешность измерения угла отскока шарика
i> - абсолютная погрешность измерения угла отскока шарика
< 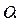 i> - усредненный угол отскока шарика
i> - усредненный угол отскока шарика
ε <  I > = ½*
I > = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(17.50/2)*0,01)2= 0,032;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(17.50/2)*0,01)2= 0,032;
ε <  2 > = ½*
2 > = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(26.50/2)*0,03)2= 0,011;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(26.50/2)*0,03)2= 0,011;
ε <  3 > = ½*
3 > = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(35.50/2)*0,04)2= 0,008;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(35.50/2)*0,04)2= 0,008;
ε <  4 > = ½*
4 > = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(430/2)*0,014)2= 0,096;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(430/2)*0,014)2= 0,096;
ε <  4 > = ½*
4 > = ½*  (0,001/0,315)2+(0,001/9,831)2+(Ctg(500/2)*0,001)2= 0,011;
(0,001/0,315)2+(0,001/9,831)2+(Ctg(500/2)*0,001)2= 0,011;
∆< 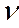 1>= 0,032 / 0,532 = 0,060 (м/c);
1>= 0,032 / 0,532 = 0,060 (м/c);
∆< 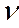 2>= 0,011 / 0,802 = 0,014 (м/c);
2>= 0,011 / 0,802 = 0,014 (м/c);
∆< 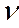 3>= 0,008 / 1,067 = 0,008 (м/c);
3>= 0,008 / 1,067 = 0,008 (м/c);
∆< 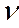 4>= 0,096 / 1,282 = 0,074 (м/c);
4>= 0,096 / 1,282 = 0,074 (м/c);
∆< 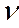 5>= 0,011 /1,479 = 0,007 (м/c);
5>= 0,011 /1,479 = 0,007 (м/c);
6.3 Определим погрешность контакта удара.
Формулы:
=  ε
ε  I 2 + ε<
I 2 + ε<  I> 2
I> 2
∆ε = εεi * εi
Производим вычисления:
εε1=  0,0152+0,0322 = 0,035; ∆ε1= 0,035*0,878= 0,030;
0,0152+0,0322 = 0,035; ∆ε1= 0,035*0,878= 0,030;
εε2=  0,0052+0,011 2 = 0,012; ∆ε2= 0,012*0,886= 0,011;
0,0052+0,011 2 = 0,012; ∆ε2= 0,012*0,886= 0,011;
εε3=  0,0052+0,0082 = 0,009; ∆ε3= 0,009*0,891= 0,008;
0,0052+0,0082 = 0,009; ∆ε3= 0,009*0,891= 0,008;
εε4=  0,0052+0,0962 = 0,096; ∆ε4= 0,096*0,866= 0,083;
0,0052+0,0962 = 0,096; ∆ε4= 0,096*0,866= 0,083;
εε5=  0,0062+0,011 2 = 0,012; ∆ε5= 0,012*1,187= 0,014;
0,0062+0,011 2 = 0,012; ∆ε5= 0,012*1,187= 0,014;
6.4 Определим погрешность средней силы удара.
Формулы:
ε 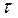 =
= 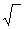 εm²+ ε<
εm²+ ε< 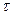 >²+ ε(
>²+ ε( i+<
i+<  i>)², ∆Fi= ε
i>)², ∆Fi= ε 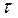 * <Fi>
* <Fi>
где;
εm = ∆m/<m>;
ε( i+<
i+<  i>)² = ∆2(
i>)² = ∆2(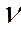 i+<
i+< 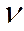 i>) / (
i>) / (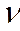 i + <
i + < 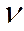 i>)2
i>)2
∆2 ( 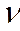 i + <
i + < 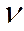 i>)2 = (∆
i>)2 = (∆ 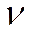 i)2 + (∆<
i)2 + (∆< 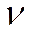 i>)2
i>)2
Производим вычисления:
ε2( 1+<
1+<  2>)=(0,024)2 +(0,060)2 / (0,605+0,532)2 = 0,0032;
2>)=(0,024)2 +(0,060)2 / (0,605+0,532)2 = 0,0032;
ε2( 2+<
2+<  2>)=(0,006)2 +(0,014)2 / (0,905+0,802)2 = 0,000075;
2>)=(0,006)2 +(0,014)2 / (0,905+0,802)2 = 0,000075;
ε2( 3+<
3+<  3>)=(0,004)2 +(0,008)2 / (1,197+1,067)2 = 0,000015;
3>)=(0,004)2 +(0,008)2 / (1,197+1,067)2 = 0,000015;
ε2( 4+<
4+<  4>)=(0,003)2 +(0,074)2 / (1,479+1,282)2 = 0,00071;
4>)=(0,003)2 +(0,074)2 / (1,479+1,282)2 = 0,00071;
ε2( 5+<
5+<  5>)=(0,003)2 +(0,007)2 / (1,757+1,479)2 = 0,0000058;
5>)=(0,003)2 +(0,007)2 / (1,757+1,479)2 = 0,0000058;
ε 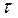 1=
1= 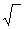 (0,003)2+(0,013)2+0,0032 = 0,058;
(0,003)2+(0,013)2+0,0032 = 0,058;
ε 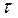 2=
2= 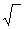 (0,003)2+(0,027)2+0,000075= 0,028;
(0,003)2+(0,027)2+0,000075= 0,028;
ε 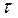 3=
3= 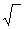 (0,003)2+(0,035)2+0,000015= 0,035;
(0,003)2+(0,035)2+0,000015= 0,035;
ε 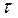 4=
4= 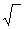 (0,003)2+(0,028)2+0,00071= 0,038;
(0,003)2+(0,028)2+0,00071= 0,038;
ε 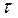 5=
5= 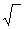 (0,003)2+(0,012)2+0,0000058= 0,014;
(0,003)2+(0,012)2+0,0000058= 0,014;
∆F1= 46,06 *0,058 = 2,67 (H)
∆F2= 69,98 *0,028 = 2,09 (H)
∆F3= 94,23 *0,035 = 3,30 (H)
∆F4= 177,02*0,038 = 6,72 (H)
∆F4= 283,82 *0,014 = 3,97 (H)
Результаты расчетов сведем в таблицу:
| <F>, H. | < 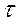 >, c. >, c.
| ε | ∆F, (H) | ∆ 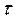
| ∆  до
удара м/c. до
удара м/c.
| ∆<  > пос-
ле удара м/c. > пос-
ле удара м/c.
| |
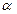 1=200 1=200
| 46,06 | 309 * 10-7 | 0,878 | 2,67 | 4,14*10-7 | 0,024 | 0,060 |
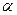 2=300 2=300
| 69,98 | 287* 10-7 | 0,886 | 2,09 | 7,75*10-7 | 0,006 | 0,014 |
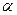 3=400 3=400
| 94,23 | 269 *10-7 | 0,891 | 3,30 | 9,43*10-7 | 0,008 | 0,008 |
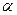 4=500 4=500
| 177,02 | 217* 10-7 | 0,866 | 6,72 | 6,23*10-7 | 0,074 | 0,074 |
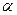 4=600 4=600
| 283,82 | 191* 10-7 | 1,187 | 3,97 | 2,28*10-7 | 0,003 | 0,007 |
Дата добавления: 2015-10-13; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Расчет погрешностей прямых измерений. | | | Р О З К Л А Д |