Задача 1. 1.Построить линейное уравнение парной регрессии

Вариант 10

х	у

Требуется:

1. Построить линейное уравнение парной регрессии от .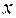

2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции с помощью -критерия Фишера и -критерия Стьюдента.

4. Оценить адекватность модели.

5. Выполнить прогноз заработной платы. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

6. На одном графике построить исходные данные и теоретическую прямую.

Предположим, что связь между х и у линейная. Для подтверждения нашего предположения построим поле корреляции.

По графику видно, что точки выстраиваются в некоторую прямую линию.

Для удобства дальнейших вычислений составим таблицу.

									, %
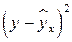
						152,579	8,421	70,907	5,230
						129,949	1,051	1,105	0,803
						135,606	-0,606	0,368	0,449
						154,465	-7,465	55,731	5,078
						142,207	-3,207	10,284	2,307
						146,922	4,078	16,633	2,701
						141,264	-6,264	39,238	4,640
						133,720	-1,720	2,960	1,303
						145,036	15,964	254,856	9,916
						150,693	8,307	68,998	5,224
						129,006	-9,006	81,101	7,505
						169,553	-9,553	91,250	5,970
Итого						1731,000	0,00	693,430	51,127
Среднзнач.	88,167	144,250		7913,833	20990,75	144,25	0,00	57,786	4,261

Рассчитаем параметры линейного уравнения парной регрессии :

;

.

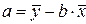Получили уравнение: . Т.е. с увеличением х на ед. у увеличится на 0.94 ед.

Уравнение линейной регрессии всегда дополняется показателем тесноты связи – линейным коэффициентом корреляции :

=

Близость коэффициента корреляции к 1 указывает на тесную линейную связь между признаками. В нашем случае связь тесная.

Коэффициент детерминации 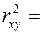0.684 показывает, что уравнением регрессии объясняется 68.4% дисперсии результативного признака, а на долю прочих факторов приходится 35.6%.

Оценим качество уравнения регрессии в целом с помощью -критерия Фишера. Рассчитаем фактическое значение -критерия:

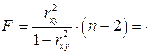
Табличное значение (, , ): 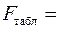4,96. Если , то признается статистическая значимость уравнения в целом. В нашем случае уравнение значимо.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем -критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции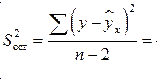

0.2

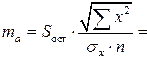18.04

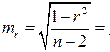
Фактические значения -статистик: =4.65 =3.39 =3,5 Табличное значение -критерия Стьюдента при и числе степеней свободы 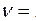10есть 2,23. Если , и 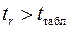, то признаем статистическую значимость параметров регрессии и показателя тесноты связи. В нашем случае параметры значимы.

Средняя ошибка аппроксимации (находим с помощью столбца 10 таблицы; 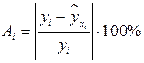) 4.261, что говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.

Оценим качество построенной модели (по двум условиям)

· отсутствие автокорреляции (по критерию Дарбина-Уотсона):

Для расчета критерия составим таблицу.

	152,579	8,421	70,907
	129,949	1,051	1,105	8,421	54,305
	135,606	-0,606	0,368	1,051	2,748
	154,465	-7,465	55,731	-0,606	47,046
	142,207	-3,207	10,284	-7,465	18,134
	146,922	4,078	16,633	-3,207	53,075
	141,264	-6,264	39,238	4,078	106,963
	133,720	-1,720	2,960	-6,264	20,644
	145,036	15,964	254,856	-1,720	312,745
	150,693	8,307	68,998	15,964	58,640
	129,006	-9,006	81,101	8,307	299,710
	169,553	-9,553	91,250	-9,006	0,299
		0,00	693,43	9,553	974,31

Критерий Дарбина-Уотсона:

;

d₁ =0,97; d₂ = 1,33

0 0,97 1,33 2,67 3,03 4

Зона положительной автокорреляции

Зона неопределенности

Отсутствие автокорреляции

Зона неопределенности

Зона отрицательной автокорреляции

Свойство независимости остатков выполняется.

• случайность остатков (по критерию пиков):

p> ;

p> 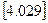; 4>4 – верно, следовательно, свойство случайности выполняется.

И, наконец, найдем прогнозное значение результативного фактора .

Для вычисления прогнозных оценок У на основе построенной моде­ли необходимо получить прогнозные оценки фактора X_.

Получим прогнозные оценки фактора на основе величины сред­него абсолютного прироста САП.

Рассчитаем САП для X:

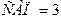
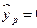
Значит, если значение х составит 118., то у будет равен 172.38 тыс. руб.

Найдем доверительный интервал прогноза. Ошибка прогноза

4.029

а доверительный интервал ():

153.812 190.951 Т.е. прогноз является статистически надежным.

Теперь на одном графике изобразим исходные данные и линию регрессии:

Задача 2. По данным задачи 1 построить нелинейные модели вида:

, ,

Найти индекс корреляции и индекс детерминации, среднюю ошибку аппроксимации, критерий Фишера. Сравнить построенные модели по индексу детерминации и средней ошибке. Выбрать наиболее качественную модель.

Построим логарифмическое уравнение регрессии .Замена приведет к линейному уравнению вида: .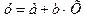

Составим вспомогательную таблицу.

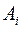
			4,575	736,528	20,928	153,342	4,756
			4,290	562,050	18,408	128,551	1,869
			4,369	589,875	19,092	135,440	0,326
			4,595	675,483	21,115	155,122	5,525
			4,454	619,154	19,841	142,845	2,766
			4,511	681,140	20,348	147,773	2,137
			4,443	599,758	19,737	141,825	5,055
			4,344	573,382	18,869	133,204	0,912
			4,489	722,670	20,148	145,835	9,419
			4,554	724,066	20,738	151,525	4,701
			4,277	513,200	18,290	127,348	6,124
			4,745	759,189	22,514	168,188	5,117
Итого			53,646	7756,497	240,028		48,709
Среднее значение	88,167	144,250	4,470	646,375	20,002	144,250	4,059

Уравнение регрессии:

Индекс корреляции: , индекс детерминации , который показывает, что 72.1% вариации результативного признака объясняется вариацией признака- фактора, а 27.9% приходится на долю прочих факторов. Средняя ошибка аппроксимации: А=4.059%. F- критерий Фишера: F_н=25.89>F_табл=4.26, следовательно уравнение статистически значимо. Изобразим график:

Построим степенное уравнение регрессии . Так как 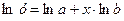, то замена ; ; приведет к линейному уравнению вида: .

Составим вспомогательную таблицу.

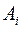
			4,575	5,081	23,246	20,928	153,098	4,908
			4,290	4,875	20,917	18,408	128,588	1,841
			4,369	4,905	21,433	19,092	134,976	0,018
			4,595	4,990	22,932	21,115	155,028	5,461
			4,454	4,934	21,980	19,841	142,196	2,299
			4,511	5,017	22,632	20,348	147,214	2,507
			4,443	4,905	21,792	19,737	141,178	4,577
			4,344	4,883	21,210	18,869	132,868	0,658
			4,489	5,081	22,809	20,148	145,220	9,801
			4,554	5,069	23,083	20,738	151,153	4,935
			4,277	4,787	20,475	18,290	127,504	6,253
			4,745	5,075	24,081	22,514	169,959	6,224
Итого			53,646	59,605	266,590	240,028	1728,982	49,483
Среднее значение	88,167	144,250	4,470	4,967	22,216	20,002	144,082	4,124

Уравнение регрессии:

Индекс корреляции: , индекс детерминации , который показывает, что 72.7% вариации результативного признака объясняется вариацией признака- фактора, а 27.3% приходится на долю прочих факторов. Средняя ошибка аппроксимации: А=4.124%. F- критерий Фишера: F_н=26.6>F_табл=4.26, следовательно уравнение статистически значимо. Изобразим график:

Построим уравнение регрессии .Замена приведет к линейному уравнению вида: .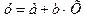

Составим вспомогательную таблицу.

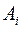
			9,849	1585,666		152,984	4,979
			8,544	1119,264		129,233	1,349
			8,888	1199,906		135,498	0,369
			9,950	1462,632		154,823	5,322
			9,274	1289,033		142,513	2,528
			9,539	1440,448		147,351	2,417
			9,220	1244,639		141,529	4,836
			8,775	1158,295		133,437	1,088
			9,434	1518,871		145,432	9,669
			9,747	1549,74		151,126	4,952
			8,485	1018,234		128,164	6,803
			10,724	1715,809		168,910	5,569
Итого			112,43	16302,54			49,881
Среднее значение	88,167	144,250	9,369	1358,545	88,167	144,250	4,157

Уравнение регрессии:

Индекс корреляции: , индекс детерминации , который показывает, что 70.4% вариации результативного признака объясняется вариацией признака- фактора, а 29.6% приходится на долю прочих факторов. Средняя ошибка аппроксимации: А=4.157%. F- критерий Фишера: F_н=23.75>F_табл=4.26, следовательно уравнение статистически значимо. Изобразим график:

Сравним построенные модели

Модель	Индекс детерминации
	0.684	4.261
	0.849	4.059
	0.853	4.124
	0.839	4.157

Наиболее хорошо исходные данные аппроксимирует модель , так как имеет максимальный коэффициент детерминации и минимальную ошибку аппроксимации.

Задача 3. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%) (смотри таблицу своего варианта).

Требуется:

1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.

3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

4. С помощью -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .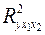

5. С помощью частных -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после .

6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Номер предприятия				Номер предприятия
		3,6				7,2
		4,1				7,6
		4,3				7,8
		4,4				7,9
		4,5				8,2
		4,8				8,4
		5,3				8,6
		5,6				8,8
		6,7				9,2
		6,9				9,6

Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:

№
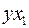
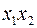
		3,6		25,2		43,2	12,96
		4,1		28,7		57,4	16,81
		4,3		30,1		68,8	18,49
		4,4		30,8		74,8	19,36
		4,5		31,5			20,25
		4,8		38,4		91,2	23,04
		5,3		42,4			28,09
		5,6		44,8			31,36
		6,7		60,3		140,7	44,89
		6,9				151,8	47,61
		7,2				165,6	51,84
		7,6		83,6			57,76
		7,8		93,6		202,8	60,84
		7,9		86,9		221,2	62,41
		8,2		98,4			67,24
		8,4		100,8		260,4	70,56
		8,6		103,2		275,2	73,96
		8,8		114,4		281,6	77,44
		9,2		119,6		303,6	84,64
		9,6		134,4		326,4	92,16
Сумма		133,5		1408,1		3399,7	961,71
Ср. знач.	9,9	6,675	23,65	70,405	249,1	169,985	48,0855	603,15	103,5

Найдем средние квадратические отклонения признаков:

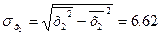
Вычисление параметров линейного уравнения множественной регрессии.

Для нахождения параметров линейного уравнения множественной регрессии

необходимо решить следующую систему линейных уравнений относительно неизвестных параметров , , :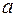

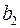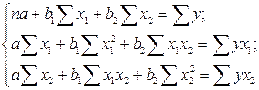
либо воспользоваться готовыми формулами:

; ;

.

Рассчитаем сначала парные коэффициенты корреляции:

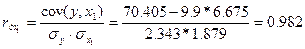
Находим

Таким образом, получили следующее уравнение множественной регрессии:

Коэффициенты 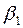и стандартизованного уравнения регрессии 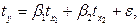находятся по формулам:

Т.е. уравнение будет выглядеть следующим образом:

Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что х2 оказывает меньшее влияние на у, чем х1.

Оценка параметров регрессии также осуществляется по методу наименьших квадратов по формуле

,

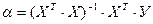Х=		3,6
		4,1
		4,3
		4,4
		4,5
		4,8
		5,3
		5,6
		6,7
		6,9
		7,2
		7,6
		7,8
		7,9
		8,2
		8,4
		8,6
		8,8
		9,2
		9,6

У=

	3,6	4,1	4,3	4,4	4,5	4,8	5,3	5,6	6,7	6,9	7,2	7,6	7,8	7,9	8,2	8,4	8,6	8,8	9,2	9,6

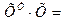
		133,5
	133,5	961,71	3399,7
		3399,7

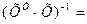
	0,693	-0,038	-0,017
	-0,038	0,282	-0,078
	-0,017	-0,078	0,023

	1408,1

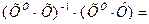
	1,69
	1,03
	0,06

В результате проведенных расчетов получаем уравнение множественной регрессии:

.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:

.

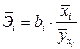Вычисляем:

;

Т.е. увеличение х1 (от своего среднего значения) или только х2 на 1% увеличивает в среднем у на 0,7% или 0,1% соответственно. Таким образом, подтверждается большее влияние на результат фактора , чем фактора .

Нескорректированный коэффициент множественной детерминации оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 96.5% и указывает на высокую степень обусловленности вариации результата вариацией факторов, иными словами – на сильную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации

Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает -критерий Фишера:

.

В нашем случае фактическое значение -критерия Фишера:

Получили, что (при 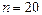), т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

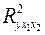Оценим качество уравнения через среднюю ошибку аппроксимации.

Для нахождения средней ошибки составим таблицу

№
		3,6		6,074	0,926	13,226
		4,1		6,702	0,298	4,256
		4,3		7,020	-0,020	0,281
		4,4		7,178	-0,178	2,549
		4,5		7,337	-0,337	4,818
		4,8		7,703	0,297	3,713
		5,3		8,276	-0,276	3,444
		5,6		8,586	-0,586	7,324
		6,7		9,779	-0,779	8,658
		6,9		10,041	-0,041	0,415
		7,2		10,407	-0,407	4,072
		7,6		10,932	0,068	0,621
		7,8		11,194	0,806	6,717
		7,9		11,408	-0,408	3,709
		8,2		11,829	0,171	1,425
		8,4		12,091	-0,091	0,761
		8,6		12,354	-0,354	2,946
		8,8		12,560	0,440	3,381
		9,2		13,030	-0,030	0,227
		9,6		13,499	0,501	3,581
Сумма		133,5		198,000	0,000	76,125

Качество построенной модели оценивается как достаточное, так как не превышает 10%.

Коэффициенты парной корреляции мы уже нашли:

; ;

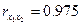
Они указывают на сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость (факторы и коллинеарны, т.к. ).

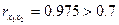Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

При двух факторах частные коэффициенты корреляции рассчитываются следующим образом:

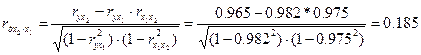
С помощью частных -критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора после и фактора после при помощи формул:

;

.

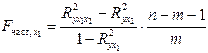Найдем 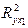и .

;

Имеем

Получили, что . Следовательно, включение в модель фактора после того, как в модель включен фактор статистически нецелесообразно.

Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения после , то результат расчета частного -критерия для показывает, что включение после статистически целесообразно, т.к. .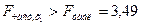

.

Дата добавления: 2015-09-05