Постановка задачи и её математическая модель

В.П. Сухинин, М.В. Горшенина

ПРОИЗВОДСТВЕННЫЙ МЕнеджмент

Методические указания к практическому занятию:

«Транспортная задача»

Сызрань 2012

УДК 658

Методические указания к выполнению практической работы / В.П. Сухинин, М.В. Горшенина; Самар. гос. техн. ун-т., филиал в г. Сызрани. Сызрань, 2012. 25 с.

Методические указания содержат сведения о содержании практического занятия по дисциплине «Производственный менеджмент». В них кратко отражены вопросы построения математической модели транспортной задачи, рассмотрены примеры решения стандартных транспортных задач и приведены задачи для самостоятельной работы.

Данные методические указания адресованы студентам, обучающимся по специальности 080502 – Экономика и управление на предприятии.

Транспортная задача

Цель работы: формирование навыков составления модели транспортной задачи и умений её решения методом потенциалов и с помощью Excel

Постановка задачи и её математическая модель

Модель транспортной задачи используется при составлении наиболее экономичного плана перевозок однородной продукции из нескольких пунктов отправления в пункты назначения, управлении запасами, назначении служащих на рабочие места и прочее.

Постановка задачи. Пусть некий однородный продукт сосредоточен у m поставщиков A_i в количествах a_i (i=1,…, m) необходимо доставить n потребителям B_j в количестве b_j (j=1,…, n).

Известна стоимость C_ij перевозки единицы груза от i -го поставщика j -му потребителю.

Требуется составить план перевозок, имеющий минимальную стоимость. Предполагаем, что стоимость транспортных расходов прямо пропорциональна объему перевозок.

Решение задачи. Пусть количество продукции, имеющейся в пункте i,составляет a_i. Количество продукции потребляемой в пункте j составляет b_j, C_ij - стоимость перевозки из пункта i в пункт j.

Пусть Х_ij – количество единиц груза, запланированного к перевозке от i -го поставщика к j -му потребителю. Математическая модель транспортной задачи имеет вид:

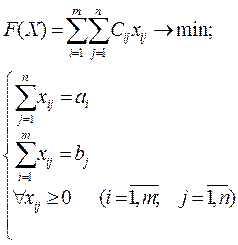(1)

Если сумма запасов 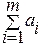равна сумме потребностей 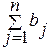,то такая модель называется сбалансированной транспортной задачей, т.е.

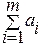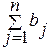= , (2)

в противном случае задача несбалансированная. Ограничения модели (1) выполняются только при сбалансированной задаче, поэтому при построении транспортной модели необходимо проверять условие баланса (2).

Если запасы превышают потребности, то есть > ,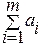

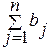то водится фиктивный пункт назначения (n +1) с потребностью

b_n+1 = - .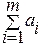

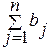Если потребности превышают запасы 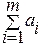< 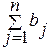, вводится фиктивный пункт отправления запасов

a_m+1 = - .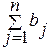

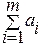Введение фиктивного потребителя или отправителя повлечет необходимость формального задания фиктивных, реально не существующих тарифов 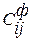для фиктивных перевозок. При этом необходимо предусмотреть, чтобы фиктивные перевозки рассматривались только после того, как будут определены все реальные перевозки. Для этого фиктивные перевозки должны стать не выгодными, то есть дорогими. Это станет возможным, если стоимость фиктивных перевозок будет превышать максимальную реальную стоимость, то есть

> .

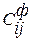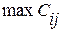На практике возможны ситуации, когда в определенных направлениях перевозки продукции невозможны (например, из-за ремонта дороги). В этом случае вводятся запрещающие тарифы 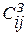, которые делают перевозки в соответствующем направлении совершенно невыгодными. Для этого величина запрещающих стоимостей должна превышать максимальную реальную стоимость, используемую в модели, то есть

> .

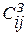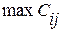Дата добавления: 2015-10-13