Предмет теории графов

Графы

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л.Эйлеру, появилась в 1736г. Вначале теория графов казалась довольно незнеачительным разделом математики, т.к. она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики особенно ее приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем электрических цепей и молекулярных схем. В настоящее время теория графов проедставляет собой раздел математики, имеющий широкое практическое значение. Можно указать и главы чистой математики, например, теория математических отношений, в которых теория графов служит естественным аппаратом; с другой стороны, эта теория находит многочисленные применения в разнообразных практических вопросах; при решении транспортных задач, задач о потоках в сети нефтепроводов; применяется в экономике, психологии, биологии; при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок-схем программ, в электротехнике, для анализа сетей связи. Математические развлечения и головоломки тоже остаются частью теории графов, особенно если отнести к ним знаменитую проблему четырех красок.

(Каждая географическая карта может быть раскрашена с соблюдением условия, чтобы страны с общей границей были раскрашены в разные цвета, при помощи четырех красок).

§1 Неориентированные графы

1. Понятие о графе

Предположим, проводятся соревнования по футболу.

Пусть общее число команд равно шести, обозначим их буквами A, B, C, D, E, F. Все команды по одному разу должны встретиться между собой. Один из вариантов схемы встреч можно изобразить так. Каждую команду представим точкой или маленьким кружочком и соединим отрезком те пары точек, которые соответствуют командам, уже игравшим друг с другом (рис.1.1).

Схема такого вида называется графом. Она состоит из нескольких точек A, B, C, D, E, F, называемыми вершинами, и нескольких соединяющих эти точки отрезков, таких, как АС, ВС, FD и т.д., называемых ребрами графа.

До начала соревнований, пока никакие игры не проводились, на графе нет никаких ребер. Такой граф состоит из одних изолированных вершин, т.е. из вершин, не соединенных никакими ребрами. Граф такого вида мы будем называть нуль-графом (рис.1.2).

Рассмотрим другой крайний случай. Предположим, что каждая команда сыграла по одному разу с каждой из оставшихся команд. Тогда на соответствующем графе каждая пара вершин будет соединена ребром. Такой граф называется полным графом (рис.1.3).

Полный граф можно представить себе как n- угольник, в котором проведены все диагонали. На рис.1.4. приведены полные графы с числом вершин n=2, 3, 4, 5.

Имея некоторый граф, например G, изображенный на рис.1.1, мы всегда можем превратить его в полный граф с теми же самыми вершинами, добавив недостающие ребра (т.е. ребра, соответствующие играм, которые еще будут сыграны).На рис.1.5 мы сделали это для графа рис.1.1.

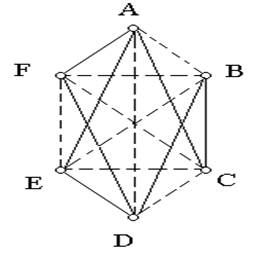
Еще не состоявшиеся игры изображены пунктиром. Можно такие отдельно начертить граф, соответствующий пока еще сыгранным, будущим играм (рис.1.6). Этот новый граф называют дополнением

графа G, обозначают G

Рис.1.5.

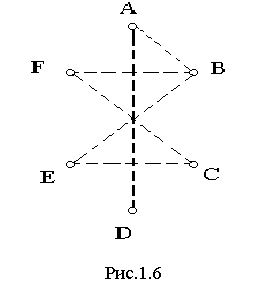
Ребра обоих графов G и G^` вместе составляют полный граф с теми же вершинами (рис.1.3, 1.5).

Математически неориентированный граф (далее: граф) определяется двумя множествами G={X,A}, где Х-конечное множество вершин (точек) х₁, х₂,...,х_n (Х_i є Х, i=1,2,...,n); A- некоторое множество ребер, соединяющих между собой все или часть этих вершин. Каждое ребро задается неупорядоченной парой вершин (x_i, x_j). Так как порядок вершин не играет роли, то наряду с записью (x_i, x_j) допустима и запись (x_j, x_i).

Рис. 7

Таким образом, граф G полностью задается и обозначается парой G={X, A}. На рис.7, имеется ребро, которое начинается и заканчивается в одной и той же вершине Х₁; такие ребра называются петлями. Некоторые пары различных вершин графа могут быть соединены несколькими ребрами, как это изображено на рис.7, такие графы называют графами с кратными ребрами. Вместо того чтобы проводить несколько ребер между одними и теми же вершинами Х₁ и Х₂ можно провести всего одно ребро, приписав ему кратность, показывающую сколько раз надо считать это ребро.

Граф называется простым, если любая пара вершин соединена не более чем одним ребром.

Две вершины называются смежными, если существует ребро, соединяющее их.

Два ребра называются смежными, если они имеют общую вершину.

Ребро (x_i, x_j) называется инцендентным каждой их вершин x_i и x_j и обратно. Вершина x_i (вершина х_j) инцидентна ребру (х_i, х_j).

Смежность является отношением между подобными элементами (между вершинами или между ребрами), тогда как инцидентность есть отношение между разнородными элементами (между вершиной и ребром).

Граф G={X, A} называется полным, если для любой пары вершин х_i и х_jєХ существует ребро (х_i, x_j)єA, то есть для каждой пары вершин существует по крайней мере одно ребро, соеденяюцее их. Иначе, граф, в котором любые две вершины смежны, называется полным. Полный граф с n вершинами обозначается через K_n. На рис.1.4 изображены графы К₂, К₃, К₄, и К₅ на рис.1.3 - граф К₆.

2. Задание графов с помощью матриц.

Для задания графов существует несколько матриц, основные из которых матрицы смежности и инцидентности.

Предположим граф G={X, A} имеет n вершин и m ребер, где конечное множество вершин - Х={х₁, х₂,..., х_n} и множество ребер А={l₁, l₂, l₃,..., l_m}.

Матрицей инцидентности графа G называется матрица R=ççr_ijçç размера nхm, у которой элементы

Принято, петле соответствует нулевой столбец. Матрица инцидентности только указывает на наличие петель в графе, но не указывает, каким вершинам эти петли инцидентны.

Например, для графа, изображенного на рис.1.9 имеем матрицу инцидентности R

Рис.1.9

Заполнить матрицу удобнее по столбцам.

Каждый столбец матрицы имеет два элемента 1, остальные - 0. Элемент 1 ставиться в строках, соответствующих вершинам, которые соединяют это ребро.

Матрица смежности графа G называется матрица Q=ççq_ijçç размера n´n, в который элемент q_ij равен числу ребер в G, соединяющих вершину х_i с вершиной х_j. Матрица смежности Q является симметрической, т.е. q_ij=q_ji.

Для графа, изображенного на рис.1.9 матрица смежности имеет вид.

Матрица смежности полностью определяет граф.

Пример. Задана симметричная матрица неотрицательных целых чисел. Нарисовать на плоскости граф G, имеющий заданную матрицу Q своей матрицей смежности. Найти матрицу инцидентности R графа G.

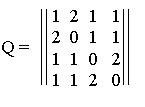
Решение Построим граф по заданной матрице смежности Q.

Рис.1.10

Теперь найдем матрицу инцидентности графа G

Петле соответствует нулевой столбец. Ребро (х₁, х₂) имеет кратность 2, поэтому ребра l₂ и l₃ имеют одинаковые столбцы, аналогично и столбцы l₈ и l₉ одинаковые.

Решение закончено.

Построенный граф G на рис.1.10 может выглядеть и иначе (рис 1.11 а и б)

а) G₁ б) G₂

Рис.1.11

Очевидно, что графы, которые могут быть изображены различным образом, могут соответствовать одним и тем же элементам некоторой системы и выражать одни и те же отношения.

3. Изоморфные графы

Заметим, что один и тот же G (рис.1.10, 1.11) можно изображать по разному.

Во-первых, совсем не обязательно изображать его ребра прямолинейными. Можно провести любые линии, соединяющие те же самые вершины, что и раньше.

Во-вторых, можно произвольно располагать вершины на плоскости.

Однако установить эквивалентность двух графов иногда очень сложно.

Определение:

Два графа, между вершинами и ребрами которых можно установить взаимно однозначное соответствие с сохранением смежности, называется изоморфными.

Операция замены графа G на изоморфный ему граф G₁ представляет деформацию графа G без разрезания ребер. Например, графы G₁ и G₂ рис.1.12 изоморфны,

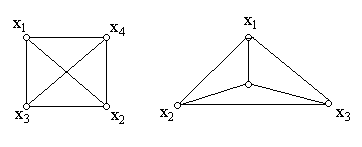
G₁ G₂

Рис.1.12

так как граф G₂ можно получить из графа G₁ путем деформации этого графа без разрезания ребер (вершину х₄ переместим во внутрь треугольника, при этом ребра деформируются).

Между вершинами и ребрами этих графов можно установить взаимно однозначное соответствие, сохраняющее смежность.

Нередко приходиться решать вопрос о том, являются ли два данных графа изоморфными. Иногда это сразу ясно, что это не так. Не могут быть изоморфными графы, имеющие разное число вершин и неодинаковое число ребер.

Пример:

Изоморфны или нет следующие пары графов?

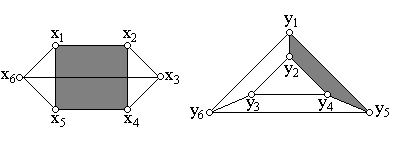
x₁«y₁, x₂«y₂, x₃«y₃, x₄«y₄, x₅«y₅, x₆«y₆.

Соответствие вершин установлено, проверим смежность вершин:

x1®x2, x5, x6;	y1®y2, y5, y6;
x2®x1, x4, x3;	y2®y1, y4, y3;
x3®x2, x4, x6;	y3®y2, y4, y6;
x4®x2, x3, x5;	y4®y2, y3, y5;
x5®x1, x4, x6;	y5®y1, y4, y6;
x6®x1, x3, x5;	y6®y1, y3, y5;

Смежность вершин сохранена. Следовательно, эти графы изоморфны.

4. Плоские графы

Определение:

Плоским графом называется граф. Который можно начертить на плоскости таким образом, чтобы его ребра не имели точек пересечения, отличных от вершин.

Для многих целей безразлично, как именно изображен граф. Изоморфные графы, доставляющие одну и ту же информацию, могут рассматриваться как один граф. Сравним два изолированных графа, изображенных на рис.1.13

Рис. 1.13

На первом из них ребра пересекаются в пяти точках, не являются вершинами графа, на втором все точки пересечения ребер графа служат его вершинами, следовательно, граф является плоским.

Плоский граф можно рассматривать как карту дорог, соединяющих между собой различные станции.

План любого города тоже является плоским графом, где улицы служат ребрами, а площади и уличные перекрестки - вершинами.

Рассмотрим одну очень старую головоломку (Задача о трех домах и трех колодцах). На одном участке земли были построены три дома и вырыты три колодца для их обитателей. Природа страны и ее климат таковы, что колодцы часто пересыхают, поэтому важно, чтобы от каждого дома имелся доступ к каждому из трех колодцев. На рис.1.14 изображен граф, отвечающий естественному расположению дорожек, когда все они прямолинейны. Дома обозначены через А, В, С,

а колодцы - X, Y, Z. Спустя некоторое время обитатели домов А, В, С поссорились друг с другом и решили проложить дорожки к трем колодцам X, Y, Z так чтобы дорожки не пересекались, чтобы им не приходилось встречать друг друга.

?

Рис.1.15

На рис.1.15 показано. Что число точек пересечения можно свести к 1. Является ли соответствующий граф плоским, т.е. можно ли провести дорожки так, чтобы они не пересекались нигде, кроме вершин графа А, В, С, X, Y, Z. Сколько ни пытайтесь, вы не найдете нужного решения. Строгое доказательство рассмотрим позже. Следовательно, граф, изображенный на рис.1.14 не является плоским.

Существует даже граф, имеющий всего пять вершин и не являющийся плоским - это полный граф с пятью вершинами (рис.1.14).

5. Цепи и циклы

Маршрутом М из Х₀ в Х_к в графе G называется конечная последовательность попарно смежных ребер вида (х₀, х₁), (х₁, х₂), (х₂, х₃),..., (х_к-1, х_к), которую будем обозначать х₀®х₁®х₂®...®х_к.

Началом маршрута считается вершина х₀, а концом маршрута - вершина х_к. Если х₀¹х_к, то маршрут незамкнутый (открытый).

Число К, входящих в маршрут М ребер, называется длиной маршрута.

Открытый маршрут называется цепью, если все ребра маршрута различны.

Маршрут называется простой цепью, если цепь с различными вершинами.

Цепь называется циклом, если цепь замкнута, т.е. х₀=х_к.

Цикл, все вершины которого различны, называется на графе (рис.1.17).

Последовательность ребер, соединяющих вершины х₀, х₁, х₂, х₃, х₄, х₅, является маршрутом. Начало маршрута в вершине х₀, а конец - в х₅, заметим ребро (х₁, х₂) проходиться дважды. Маршрут х₀, х₁, х₂, х₃, х₄, х₅, является цепью, при этом вершина х₂ проходится дважды. Цепь х₀, х₁, х₂, х₃, х₄, х₅, является простой цепью. Цепь х₁, х₂, х₃, х₄, х₅, х₁, является циклом (вершина х₂ пройдена дважды). Цепь х₁, х₂, х₃, х₄, х₅, х₁, является простым циклом.

6. Связанность и подграфы

Определение:

Граф G={Х, А} называется связным (связанным), если между произвольными различными двумя его вершинами существует цепь

Все рассмотренные ранее графы, за исключением графов на рис. 2 и 8, были связными.

У несвязного графа не все вершины соединены цепью (рис.1.18).

Рис.1.18

У графа (рис.1.18) не все вершины можно соединить цепью, например, между вершинами х₁ и х₅, х₁ и х₁₀ и т.д. Граф, представленный на рис1.18 не является связанным. Его множество вершин Х={х₁, х₂, х₃, х₄, х₅, х₆, х₇, х₈, х₉, х₁₀} и множество ребер А={(х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₁), (х₅, х₆), (х₆, х₇), (х₇, х₈), (х₈,х₆), (х₉, х₁₀)}.

Пусть V_i - недопустимое подмножество множества вершин Х графа G={X,A}. Например, V₁={х₁, х₂, х₃, х₄}; V₂={х₅, х₆, х₇, х₈}; V₃={х₉, х₁₀}.

Обозначим через A(V_i|) совокупность ребер графа, обе концевые точки которых принадлежат V_i.

Например, A(V₁)={ (х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₁)}; A(V₂){ (х₅, х₆), (х₆, х₇), (х₇, х₈), (х₈,х₆)}; A(V₃)={(х₉, х₁₀)}.

Граф G_i={V_i, A(V_i)} называется подграфом графа G.

На множестве вершин графа G={Х, А} определим отношение «», считая, что х_i x_j, если x_i=x_j, или в графе существует цепь, соединяющая x_i и x_j. Это отношение является отношением эквивалентности.

Очевидно, V₁, V₂, V₃ - классы эквивалентности множества вершин Х графа G={Х, Ф}.

Определение:

Если подмножества V_i представляют классы эквивалентности множества вершин Х, то подграфы G_i={V_i, A(V_i)} графа G называются связными компонентами этого графа, а их число К называется степенью связности.

Граф, представленный на рис.1.18 имеет 3 связных компоненты {V₁, A(V₁)}, {V₂, A(V₂)}, {V₃, A(V₃)} и его степень связности равна 3. Весь граф разлагается в сумму своих связных компонент.

Очевидно, что степень связности связного графа равна 1 и его единственная связная компонента совпадает с самим графом.

Определение:

Остовным подграфом графа G называется граф G_y={X, A_y}, для которого A_yÌA.

Т.е. остовный подграф имеет тоже множество вершин, что и граф G, но множество ребер подграфа G_y является подмножеством множества ребер А исходного графа. На рис. 1.19 а) изображен исходный граф G={X, A}; на рис.1.19 б) - остовный подграф G₁ графа G и на рис.1.19 в) - подграф G₂ графа G.

Рис.1.19

Остовный подграф G, имеет множество вершин Х={х₁, х₂, х₃, х₄, х₅}, совпадающие с множеством графа G, и множество ребер А={(х₁, х₂), (х₂, х₃), (х₃, х₄), (х₄, х₅)}, являющиеся подмножеством множества А исходного графа. Подграф G₂ имеет подмножество V₂ множества вершин Х (V₂={x₁, x₂, x₃, x₅}) и подмножество ребер А₂{(х₁, х₂), (х₁, х₃), (х₃, х₅)}.

Определение:

Граф G={Х, А} называется двудольным, если множество его вершин Х можно разбить на два непересекающихся подмножества V₁ и V₂ таких, что каждое ребро имеет один конец в V₁, а другой в V₂.

Примером двудольного графа является граф, изображенный на рис.1.14. Одно подмножество вершин V₁={A, B, C}, второе - V₂={X, Y, Z}.

Определение:

Двудольный граф G={V₁ÈV₂, A} называется полным двудольным графом, если каждая вершина подмножества V₁ соединена ребром с каждой вершиной подмножества V₂.

Если число вершин подмножеств V₁ и V₂ равно соответственно r и s, то полный двудольный граф обозначается K_r,s. Граф, изображенный на рис.1.14, является полным двудольным графом; обозначим его через K_3,3.

Напомним, что этот граф не является плоским.

Полные графы с n вершинами ранее обозначали через К_n (рис.1.3, 1.4, 1.5).

Примерами неплоских графов, которые играют важную роль в теории плоских графов, являются: полный граф с пятью вершинами К₅ и полный двудольный граф К_{3, 3}.

Теорема:

Граф G={X, A} является плоским тогда и только тогда, когда никакой его подграф не совпадает с К₅ и К_{3, 3}.

7. Эйлеровы и гамильтоновы графы

Первая работа о графах, принадлежащая швейцарскому математику Леонарду Эйлеру (1707 - 1783), появилась в 1736 г. в публикациях Петербургской Академии наук. В 1727 г., когда ему едва исполнилось 20 лет, он был приглашен в Российскую Академию наук. Он добился блестящих успехов в математике, физике, астрономии; написал огромное количество работ. К тому времени, когда он написал работу о графах, он потерял зрение на один глаз, а к старости совершенно ослеп, но даже это не остановило потока его работ.

Эйлер начал свою работу о графах с рассмотрения одной головоломки - так называемой задачи о «Кенигсбергских мостах». Город Кенигсберг (ныне Калининград) расположен на берегах реки Прегель (Преголи) и двух островах. Различные части города были соединены семью мостами (рис.1.20)

Рис.1.20

По воскресеньям горожане совершали прогулки по городу. Вопрос заключался в том, можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно пройдя в точности один раз по каждому мосту?

Схематически карта изображена на рис.1.20.

Четыре части города обозначены буквами А, В, С, D.

Так как нас интересует только переходы по мостам мы можем считать А, В, С, D вершинами некоторого графа, ребра которого отвечают соответствующим мостам. Этот граф изображен на рис.1.21

Рис.1.21

Эйлер показал, что этот граф не представляет собой единого цикла; иными словами, с какой бы вершины ни начали обход, не сможем обойти весь граф и вернуться обратно, не проходя никакого ребра дважды.

Ведь если такой цикл существовал, то в каждой вершине графа было бы столько же входящих в нее ребер, сколько и выходящих из нее, т.е. в каждой вершине графа было бы четное число ребер. Однако это условие не выполнено для графа, представленного на рис.1.21.

Цикл называется эйлеровым, если каждое ребро графа участвует в его образовании один раз. Граф, содержащий такой цикл, называется эйлеровым.

Возникает вопрос: можно ли найти необходимые и достаточные условия для того, чтобы граф был эйлеровым. Ответ дает теорема.

Теорема:

Граф G={X, A} является эйлеровым тогда и только тогда, когда он связан и степень каждой вершины r(х_i) - четное число.

Итак, эйлеров граф представляет собой единый цикл, каждое ребро его участвует один раз в цикле, при этом одна и та же вершина может быть пройдена несколько раз.

Эйлеровым графом должен был быть и план любой выставки: вдоль ее помещений можно было бы расставить знаки, показывающие, как именно посетители должны двигаться, чтобы осмотреть каждый экспонат в точности по одному разу. Эйлеров граф можно нарисовать не отрывая карандаша от бумаги и не проводя никакого ребра дважды. Для эйлерова графа выполнение такого рисунка начинается и заканчивается в одной и той же вершине.

В 1859 г. известный ирландский математик сэр Уильям Роуэн Гамильтон выпустил в продажу головоломку. Ее основной частью был правильный додекаэдр, его гранями служат 12 правильных пятиугольников, причем в каждой из 20 его вершин сходиться по три ребра. Каждая вершина помечена названием одного из крупных городов. Задача состояла в нахождении пути вдоль ребер, проходящего через каждый город в точности по одному разу. Гамильтоновой линией на графе называется цикл, проходящий через каждую вершину графа в точности по одному разу. Он не показывает, вообще говоря, всех ребер; ведь в каждой вершине он проходит в точности по двум ребрам. Как видим, имеется аналогия между эйлервыми и гамильтоновыми линиями. Первая проходит один раз по каждому ребру, вторая - через каждую вершину.

Итак, цикл называется гамильтоновым, если каждая вершина графа участвует в его образовании только один раз. Граф, содержащий такой цикл называется гамильтоновым. Граф, который содержит простую цепь, проходящую через его вершину, называется полугамильтоновым. На рис.1.23 изображены соответственно негамильтонов, полугамильтонов и гамильтонов графы.

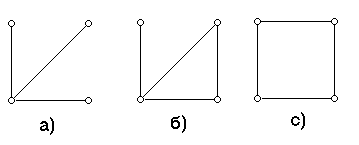
Рис.1.23

8. Деревья и лес

Деревом называется связный граф, не содержащий простых циклов. Такой граф, в частности, не имеет и кратных ребер.

Рис.1.24

Из определения дерева вытекает также, что для каждой пары его вершин существует его единственная соеденяющая их цепь.

Деревья имеют многочисленные применения. Упомянем лишь один. Граф, приведенный на рис.1.24, может представлять процесс сортировки писем на главпочтамте. Первоначально пачка писем поступает на главпочтамт (х₀), там почта дробиться на три района х₁, х₂, х₃, на районных почтовых отделениях снова дробиться по почтовым отделениям и т.д.

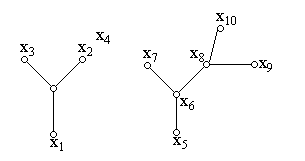
Рис.1.25

Если граф не связный, не содержит циклов, то каждая его связная компонента будет деревом (рис.1.25). Пользуясь терминологией, принятой в ботанике такой граф можно назвать лесом.

Итак, произвольный граф. Не содержащий циклов называется лесом, а его связные компоненты называются деревом.

Простейшее дерево имеет только одно ребро и две вершины. Если мы добавим еще одно ребро, то прибавляется также и вершина, следовательно, справедлива теорема.

Теорема:

Дерево с n вершинами имеет n-1 ребер.

Вместо одного дерева рассмотрим теперь лес, состоящий из К связных компонент, каждая из которых является деревом (рис.1.26).

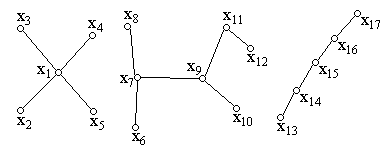
Рис.1.26

Для каждой из компонент число ребер на единицу меньше числа вершин. Следовательно, справедлива теорема.

Теорема:

Лес, состоящий из К компонент и имеющий n вершин, содержит n-k ребер.

В следующей теореме перечислены некоторые простые свойства деревьев.

Теорема:

Пусть граф G имеет n вершин. Тогда следующие утверждения эквивалентны:

1) G является деревом;

2) G не содержит циклов и имеет (n-1) ребер;

3) G связан и имеет (n-1) ребер;

4) любые две вершины графа G соединены только простой цепью;

5) G не содержит циклов. Но добавляя к нему только одно новое ребро, получим ровно один цикл;

6) G связен и каждое его ребро является мостом.

Поясним последнее свойство.

Рассмотрим произвольный граф, представленный на рис.1.27. Пусть х- некоторое ребро графа G, граф G - х получается путем удаления из G ребра х (обе концевые вершины в графе остаются).

Рис.1.27

Ребро х графа G={X, A} называется мостом или разделяющим ребром, если связность G-x больше связности G. На рис.1.27 связность графа G равна 1, а связность графа G-x равна 2, следовательно, ребро х является мостом.

Очевидно, удаление любого ребра из дерева делает его несвязным.

9. Цикломатическое число графа

Пусть дан произвольный связный граф G={X, A}.

Для него можно составить остовные подграфы G₁={X, A₁}, G₂={X, A₂},..., G={X, A_k}. (Оставный подграф имеет тоже множество вершин, что и граф G, а множество ребер A_yÌA). Среди остовных подграфов могут быть и деревья.

Дерево, являющееся остовным подграфом графа G, называется остовным деревом или остовом.

Например: Дан граф G={X, A}, где X={x₁, x₂, x₃, x₄, x₅}.

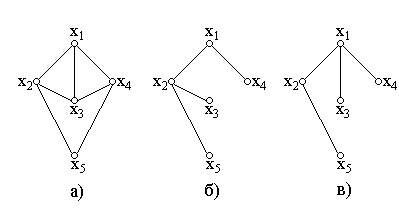
Рис.1.28

На рис.1.28 изображен граф G и его два остова б), в).

Можно привести и другие варианты остовных деревьев.

Теорема:

В связном графе всегда существует остовное дерево.

Доказательство:

Если в графе нет циклов, то он является деревом и, следовательно, сам себя покрывает. При наличии циклов исключим из графа ребра, образующие циклы, (рис.1.28) и придем к подграфу, не содержащему циклов. Этот подграф и будет остовным деревом.

Пусть произвольный связный граф имеет n вершин и m ребер. Все остовные деревья будут иметь n вершин и (n-1) ребер. А теперь легко подсчитать, сколько ребер нам пришлось удалить.

Определение:

Число удаленных ребер в процедуре образования остовного дерева называется цикломатическим числом (циклическим рангом) и обозначается g(G).

g(G)=m-(n-1)=m-n+1;

Цикломатическое число определяет меру связности графа. На рис.1.28 g(G)=3.

Очевидно, цикломатическое число графа является целым неотрицательным числом. Граф является деревом тогда и только тогда, когда его цикломатическое число равно 0.

Если граф содержит К компонент связности, то его цикломатическое число

g(G)=m-(n-k)=m-n+k.

10. Хроматическое число графа.

Другой характеристикой графа G является хроматическое число, связанное с раскрашиванием графа.

Раскрашиванием графа называют процесс сопоставления его вершин цветов, при котором любые две соседние (смежные) вершины оказываются разноцветными. Минимальное число цветов, необходимых для такой раскраски графа, называют хроматическим.

Хроматическое число связано с раскрашиванием карт. Пусть дана географическая карта. Требуется окрасить каждое государство так, чтобы любые два государства, граничащие между собой, были окрашены в разные цвета. Если в нашем распоряжении имеется достаточное количество различных красок, то это не составит никакого труда. Намного сложнее решить вопрос о наименьшем количестве красок, достаточном для такого раскрашивания. Эта проблема была очень популярна в прошлом столетии, ею занимались известные математики.

Доказана теорема о пяти красках. Любой плоский граф можно раскрасить пятью красками.

Также удалось доказать, что с помощью четырех красок можно осуществить правильную раскраску для плоских графов с числом вершин не превосходящих 38.

В терминах графов задача может быть поставлена следующим образом. Дан произвольный плоский граф G без петель. Имея некоторое количество красок l необходимо раскрасить каждую вершину одной из этих красок так, чтобы любые две смежные вершины имели различную окраску. Если граф G является l раскрашиваемым, но не является (l-1)- раскрашиваемым, то называют его l - хроматическим, а число l называют хроматическим числом графа G и обозначают À(G)=l.

Рис.1.29

На рис.1.29 изображен 4-хроматический граф. Цвета обозначены греческими буквами a, b, g, d.

§2. Ориентированные графы

1. Понятие об ориентированном графе

В §1, введя понятие о графе, мы рассматривали в качестве примера состязания футбольных команд A, B, C, D, E, F. Все команды по одному разу должны встретиться между собой. Команды уже игравшие соединим ребрами, и таким образом, получили неориентированный граф (рис.2.1).

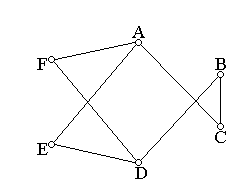
Рис.2.1

Однако такой граф не дает ответа на вопрос: кто именно выиграл эту игру? Этот недостаток может быть устранен. Если команда А выиграла у команды С, условимся ставить на ребре АС стрелку, направленную от А к С. Предположим, что нам известны результаты всех уже сыгранных игр (ничейные результаты исключены) и вдобавок к графу рис.2.1 соответствующие стрелки, пусть при этом получиться граф, изображенный на рис.2.2.

Рис.2.2

На это графе показано, что команда А выиграла у команд С и F, но проиграла команде Е; команда В выиграла у команд С и D; а команда D проиграла командам В, Е, F, и т.д. Граф, на котором указано направление каждого его ребра, называется ориентированным графом (сокращенно орграф).

Если же ничейные результаты неизбежны, можем отразить их на графе, оставляя соответствующие ребра неориентированными. При это получиться так называемый смешанный граф, на котором имеются как ориентированные, так и неориентированные ребра.

План транспортных магистралей города дает нам несколько специальный, но зато наглядный пример графа. На современном плане города должны быть показаны не только относительное расположение улиц и их пересечений, так же и то, на каких улицах имеется двусторонний поток транспорта, а на каких - одностороннее движение, причем в последнем случае должно быть показано направление движения. На улицах с двусторонним движением неориентированное ребро можно заменить двумя ориентированными ребрами, соединяющими те же самые вершины А и В и имеющими противоположные направления (рис.2.3).

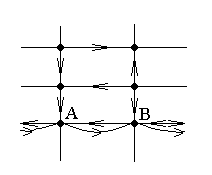
Рис.2.3

Математически неориентированный граф G определяется двумя множествами: X={x₁, x₂,..., x_n} - конечное множество вершин, А - конечное множество дуг (х_i, x_j), соеденяющих между собой все или часть вершин. Каждая дуга (x|_i, x_j) задается упорядоченной парой вершин x_i, x_j, т.е. дуга выходит из вершины x_i и входит в вершину x_j. Дуга (x_i, x_j) называется ориентированной, при этом вершина x_i называется начальной, а x_j - конечной вершиной.

Формально ориентированный граф G={X, A} определяется как множество вершин Х и множество А ориентированных дуг. Ориентированный граф будем называть кратко орграф. Дуга (x_i, x_j) с концами в одной и той же вершине называется петлей. Граф, у которого нет петель, называется графом без петель. На рис.2.4 представлен орграф G={X, A}, где X={x₁, x₂, x₃}, A={(x₁, x₁), (x₁, x₂), (x₁, x₃), (x₃, x₂)}.

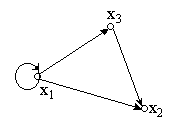
Рис.2.4

2. Задание орграфа с помощью матриц

Понятие о смежности и инцидентности распространяется на ориентированные графы.

Две вершины называются смежными, если существует дуга соединяющая их.

Две дуги называются смежными, если они имеют общую вершину.

Дуга (x_i, x_j) называется инцидентной каждой из вершин x_i и x_j.

Вершина x_i называется инцидентной дуге, входящей в эту вершину или исходящей из этой вершины.

Предположим орграф G={X, A} имеет n вершин и m дуг. X={x₁, x₂,..., x_n}. Пронумеруем дуги l₁, l₂,..., l_m.

Матрицей смежности орграфа G={X, A} c множеством вершин Х называется матрица В=ççb_ijçç (i=1, 2,..., n; j=1, 2,..., n), в которой элемент b_ij равен числу дуг вида (x_i, x_j), идущих от вершины x_i к вершине x_j.

Например, составим матрицу смежности для орграфа, представленного на рис.2.7

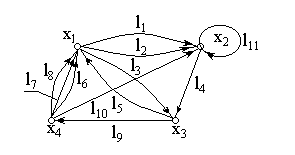
Рис.2.7

Составим 1-ю строку матрицы смежности:

b₁₁=0, т.к. при вершине х, нет петель;

b₁₂=2, т.к. из вершины х, выходят 2 дуги к х₂;

b₁₃=1, т.к. из х₁ выходит одна дуга к х₃;

b₁₄=0, т.к. нет дуг, выходящих к х₄.

Составим 2-ю строку:

b₂₁=0, т.к. из х₂ к х₁ нет дуг;

b₂₂=1, т.к. при вершине х₂ есть одна петля;

b₂₃=1, т.к. одна дуга выходит из х₂ к х₃ и т.д. Получим

Матрица смежности полностью определяет орграф.

Заметим, что матрица смежности орграфа в общем случае не является симметрической. А матрица смежности неориентированного графа есть симметрическая матрица.

Матрицей инциндентности орграфа G={X, A} c множеством вершин X={x₁, x₂,..., x_n} и множеством дуг A={l₁, l₂,..., l_m} матрица C=ççC_ijçç размера n´m, у которой

Каждый столбец этой матрицы имеет один элемент +1 и один элемент -1, а все остальные элементы столбца равны 0.

Например, составим матрицу инцидентности для орграфа представленную на рис.2.7

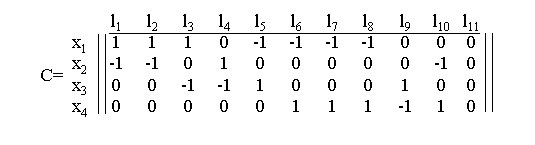
Петле l₁₁ соответствует нулевой столбец. Матрица инцидентности только указывает на наличие петель в орграфе, но не указывает, каким вершинам эти инцидентны.

Если орграф C_ij одновременно равен +1 и -1, что приводит к неоднозначности элементов матрицы С.

Для задания графа с петлями «расщепим» матрицу С на две матрицы С⁺ и С^-

Если граф без петель, то С=С⁺ - С^-.

Для графа, представленного на рис.2.7 составим матрицы смежности С⁺ (начала дуг) и С^- (конца дуг).

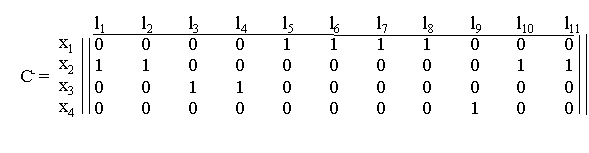
Если одну матрицу наложить на вторую, то там, где единицы совпадают, это соответствует петле; петля находиться в вершине х₂.

3. Путь и контур

Последовательность дуг ориентированного графа называется путем, если конец предыдущей дуги является началом следующей дуги. Так, например в орграфе на рис.2.8 последовательность дуг: (х₁, х₂), (х₂, х₅), (х₅, х₄), (х₄, х₃) является путем из вершины х₁ в вершину х₃.

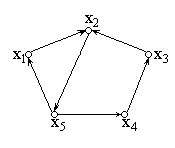
Рис.2.8

Число дуг, образующих путь, называется длиной пути.

Путь называется составным, если в нем повторяется хотя бы одна дуга, сложным, если в нем повторяется хотя бы одна вершина, и простым - в противном случае.

Контуром называется путь начальная и конечная вершины которого совпадают. Так последовательность дуг: (х₂, х₅), (х₅, х₄), (х₄, х₃), (х₃, х₂) является контуром.

Число дуг. образующих контур, называется длиной контура. Петля - это контур единичной длины.

Таким образом, для орграфа введены понятия:

дуга, путь, контур, а для неориентированного графа аналогичные понятия:

ребро, цепь, цикл.

Пример. Из лагеря вышли 5 туристов: Василий, Галина, Анатолий, Елена и Михаил. Анатолий идет впереди Михаила, Елена - впереди Василия, но позади Михаила, Галина впереди Анатолия. Кто идет первым и кто последним?

Решение. Попробуем решить построением орграфа отношения a:’x идет сзади y’.

Рис.2.15

На плоскости отметим 5 точек, которые обозначим первыми буквами имен туристов (рис.2.15). От x проведем стрелку к y.

По тексту МaА, ВaЕ, ЕaМ, АaГ, проводим стрелки и получим орграф. Первой идет Галина, а последним - Василий.

6. Достижимость и связность

Рассмотрим орграф G={X, A}.

Если соответствующий ему неориентированный граф G={X, A} является связным, то орграф G называется слабо связным.

Другими словами, слабая связность означает, что пренебрегая ориентацией ребер, можно из любой вершины графа по ребрам дойти до любой другой вершины.

Вершина x_j орграфа G называется достижимой из вершины x_i, если x_i=x_j или существует простой путь из x_i в x_j.

Орграф G называется сильно связным, если любая его вершина достижима из любой другой вершины. Пример сильно связного графа приведен на рис.2.16.

Рис.2.16

Очевидно, сильно связный граф является с слабо связным графом.

Обозначим через S₁, S₂, S₃,..., S_k классы эквивалентности, получающиеся при разбиении множества вершин Х орграфа G={X, A} с помощью отношения эквивалентности, введенного ранее. Графы (S₁, A(S_k)),..., (S_k, A(S_k)) (подграфы), получающиеся из множеств S₁, S₂,..., S_k называются сильносвязными компонентами графа G; при этом множества A(S_i) представляет собой множество ориентированных дуг из А, начинающихся и заканчивающихся в вершинах множества S_i.

Рассмотрим пример. На рис.2.17 а) приведен орграф G.

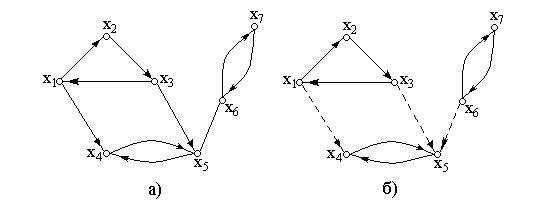
Рис.2.17

Выделим классы эквивалентности множества вершин S₁={x₁, x₂, x₃}, S₂={x₄,x₅}, S₃={x₆, x₇}. Сильно связными компонентами будут три ориентированных подграфа, которые получаются после удаления из рассматриваемого графа дуг, показанных на рис.2.17 б) пунктирными линиями.

Если орграф G является сильно связным, то, очевидно, его единственный сильно связный компонентой будет он сам.

7. Ориентированные деревья

Вершина х₀ ориентированного графа G называется его корнем, если любая другая вершина достижима из х₀ (рис.2.18).

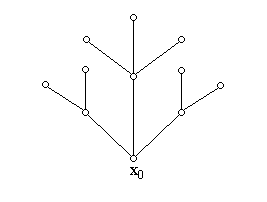
Рис.2.18

Ориентированный граф G={X, A} называется ориентированным деревом, если он имеет корень и соответствующий ему неориентированный граф G={X,A}

является деревом.

Теорема:

Ориентированное дерево имеет только один корень.

Доказательство:

Если предположить, что имеются два корня х₁ и х₂: то существует путь (х₁®х₂) и наоборот (х₂®х₁), то есть имеем контур (цикл).

Но по определению дерево не имеет циклов. Пришли к противоречию, следовательно, два корня не могут быть.

Пусть S - множество вершин, достижимых из вершины а. Рассмотрим подмножество {S, A(S)}. Нетрудно проверить, что этот граф является ориентированным деревом с корнем а. Это дерево называется ориентированным поддеревом графа G (рис.2.19 б)).

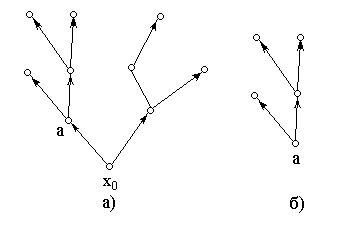
8. Взвешенный граф

При решении технических и хозяйственных задач приходиться вводить взвешенный граф.

Например, хотим построить сеть дорог, которые соединили бы n данных городов, причем так, чтобы пассажир мог проехать из каждого города в любой другой.

Для каждой пары городов (х, у) известна стоимость l(x, у) строительства соединяющей их дороги. Задача состоит в том, чтобы построить самую дешевую из возможных сетей дорог. Вместо сети дорог можно рассматривать сеть линий электропередач, газопроводов и т.д.

Таким образом, для каждого ребра графа (х_i, x_j)ÎA определим неотрицательное число l_ij, которое назовем весом или длиной ребра (x_i, x_j).

Аналогично, по степени значимости городов можно ввести каждой вершине графа вес W_i.

В результате получим взвешанный граф G с множеством взвешанных вершин W_i (i=1, 2,..., n) и множеством взвешанных ребер {(x_i, x_j)| l(x_i, x_j)}.

Взвешанный граф представляет собой граф плюс функции, определенные на вершинах и ребрах.

\

§3. Оптимизационные задачи на графах

1. Построение остовного дерева минимальной длины. Алгоритм Краскала построения минимального дерева.

Большое практическое значение имеет следующая задача, которую можно сформулировать в виде задачи о проведении дорог.

Представим, нужно построить сеть железных дорог, которые соединили бы n данных городов, причем так чтобы пассажир мог проехать из каждого города в любой другой. Для каждой пары городов известна стоимость l(х, у) строительства соединяющей их дороги.

Задача состоит в том, чтобы построить самую короткую из всех возможных дорог. Называя в графе, изображающем сеть дорог, величину l(х, у) длиной ребра, соединяющего города х и у, приходим к задаче о построении графа наименьшей длины.

Ясен, что граф, вершины которого соответствуют городам, а ребра - соединяющим их железным дорогам, должен быть деревом. Задача состоит в нахождении алгоритма, определяющего, какое из возможных n^n-2 деревьев, соединяющих эти города, будет наименьшей длины.

Алгоритм, известный под названием алгоритма Краскала, дает следующая теорема.

Теорема:

Пусть G - связный граф с n вершинами. Тогда следующая процедура приводит к остовному дереву наименьшей длины:

1) выберем ребро l₁, обладающее в G наименьшей длиной;

2) определим по индукции последовательность ребер l₁, l₂,..., l_n-1, выбирая на каждом шаге ребро с наименьшей мерой, обладающее тем свойством, что подграф Т графа G, ребрами которого являются l₁, l₂,...,l_n-1, и есть требуемое остовное дерево.

Пример. Расстояние между городами A, B, C, D, E, F в сотнях километрах дано в таблице.

Требуется построить сеть железных дорог так, чтобы количество затраченных рельсов было минимальным и пассажир мог из каждого города проехать в любой другой город.

Решение. Построим граф G с 6 вершинами, соответствующим 6 городам A, B, C, D, E, F.

Рис.3.1

Соединим каждую вершину со всеми остальными. Получим полный граф G=K₆.

Число ребер полного графа m=1/2n(n-1)=1/2·6·5=15

На каждом ребре графа (согласно таблице) проставим расстояние между соответствующими городами (рис.3.1). Эту цифру называют мерой (весом) соответствующего ребра, например. l(С, D)=3.2

Теперь наша задача будет состоять в определении одного из возможных n^n-2=6^6-2=6⁴=1296 деревьев, соединяющих данные города. Это остовное дерево Т должно иметь наименьшую сумму мер его ребер (сумма берется по всем ребрам дерева Т).

Число ребер в исходном дереве Т можно определить, зная цикломатическое число графа G=K₆. Цикломатическое число графа

g(G)=m-n+k,

где m-число ребер, n-число вершин; k-число компонент связности графа.

Для данного графа m=15, n=6, k=1.

g(G)=15-6+1=10;

Следовательно, в графе нужно убрать 10 ребер, чтобы получить остовное дерево, которое будет иметь 15-10=5 ребер.

Для того, чтобы построить для графа G остовное дерево Т наименьшей длины, воспользуемся алгоритмом Краскала, который сформулирован в теореме.

1) Выбираем ребро наименьшей длины: l(EF)=2.

2) Выбираем ребро, у которого наименьшая длина. Это ребро АС, l(АС)=3 (рис.3.2).

Рис.3.2

3) Выбираем из оставшихся 13 ребер ребро наименьшей длины. Это ребро CD, l(CD)=3.2.

4) Из оставшихся 12 ребер выбираем ребро с наименьшей длиной при условии, что оно не образует цикла (исключим из рассмотрения ребро AD). Это ребро ВА, l(ВА)=3.6.

5) Исключим из рассмотрения ребра ВС и АD, образующие циклы. Из оставшихся ребер наименьшую длину имеет ребро АЕ, l(АЕ)=4.

Алгоритм закончен. На графе (рис.3.2) приведено остовное дерево Т. Длина остова Т:

l(FE)Èl(AE)Èl(AB)Èl(AC)Èl(CD)=2+4+3.6+3+3.2=15.8

Дата добавления: 2015-10-13