Определение длин рельсовых нитей стрелочного перевода

Длину рельсовых нитей стрелочного перевода находят по формулам:

l₁ = L_п – l_рр - d, (1.29)

l₂ = 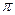/180(R+b_г/2)(a-b_н) + к – n - l₀ - 2d, (1.30)

l₃ = L_т - l'₀ – n - 2d, (1.31)

l₄= q - S_остр sinb_н+3,14/180(R - S_к - b_г/2)(a-b_н) + к + m - l_рр- d, (1.32)

где S_остр, S_k - ширина колеи в начале остряков и в переводной кривой, мм;

d - зазор, равный 8 мм.

При S_остр = S_k = 1520 мм:

l₁ = 35611 – 10929 – 8 = 24674 мм,

l₂ = 0,017453*(495888 + 73/2)*(4,398611 – 1,216667) + 2232 – 1232-

- 5942 – 16 = 22583 мм,

l₃ = 29728 – 5940 - 1232 -16 = 22540 мм,

l₄= 2919 - 1520*0,021233 + 0,017453*(495888 -1520 -73/2)*

*(4,398611 – 1,216667) + 2232 + 2964 - 10929 – 8 = 24598 мм.

l’₁, l’₂, l’₃, l’₄ – длины рельсов за корнем остряков, принимаем равными или

6250, или 12 500, или 25 000 мм;

Рисунок 1.8 - Расчетная схема для определения длины рельсовых нитей стрелочного перевода

1.7 Построение схемы разбивки стрелочного перевода

На основе полученных расчетом величин вычерчивают схему стрелочного перевода в масштабе 1:100.

Вначале на чертеж наносят ось прямого пути перевода и отмечают на ней центр перевода. От центра перевода откладывают в масштабе осевые размеры a, b, a_0, b₀, затем определяем положение математического центра

крестовины, характеризуемое величинами b₀ и S₀/2. Из математического центра крестовины описывают дугу радиусом, равным S₀/2, и, проведя к ней касательную из центра перевода, находят направление оси бокового пути. После этих геометрических построений вычерчивают в масштабе в рабочих гранях рельсов стрелочный перевод и отмечают на нем стыки. Наружную нить переводной кривой наносят на чертеж по вычисленным значениям ординат, а внутреннюю - на основе заданной ширины колеи.

На эпюре и схеме разбивки стрелочного перевода указывают основные геометрические размеры стрелочного перевода, длину рельсов и ширину колеи в соответствующих местах перевода. Под схемой перевода размещают спецификацию длин рельсов.

Дата добавления: 2015-09-03