
|
Читайте также: |
В 1963 г. американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель Шарпа (Sharpe single-index model).
В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две переменные величины - независимую X и зависимую Y линейным выражением типа  модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал норму отдачи
модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал норму отдачи  , вычисленную на основе индекса Standart and Poors (S&P500). В качестве зависимой переменной берется отдача
, вычисленную на основе индекса Standart and Poors (S&P500). В качестве зависимой переменной берется отдача  какой-то i-ой ценной бумаги. Поскольку зачастую индекс S&Р500 рассматривается как индекс, характеризующий рынок ценных бумаг в целом, то обычно модель Шарпа называют рыночной моделью (Market Model), а норму отдачи
какой-то i-ой ценной бумаги. Поскольку зачастую индекс S&Р500 рассматривается как индекс, характеризующий рынок ценных бумаг в целом, то обычно модель Шарпа называют рыночной моделью (Market Model), а норму отдачи  - рыночной нормой отдачи.
- рыночной нормой отдачи.
Пусть норма отдачи  принимает случайные значения и в течение N шагов расчета наблюдались величины
принимает случайные значения и в течение N шагов расчета наблюдались величины  ,
,  ,…,
,…,  . При этом доходность
. При этом доходность  какой-то i-ой ценной бумаги имела значения
какой-то i-ой ценной бумаги имела значения  ,
,  ,…,
,…,  . В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами
. В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами  и
и  в любой наблюдаемый момент времени в виде:
в любой наблюдаемый момент времени в виде:
 (54)
(54)
где: 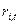 – доходность i-ой ценной бумаги в момент времени t;
– доходность i-ой ценной бумаги в момент времени t;
 – параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг
– параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг  ;
;
 – параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности;
– параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности;
 – доходность рыночного портфеля в момент t;
– доходность рыночного портфеля в момент t;
 – случайная ошибка, свидетельствующая о том, что реальные, действующие значения
– случайная ошибка, свидетельствующая о том, что реальные, действующие значения 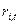 и
и  порою отклоняются от линейной зависимости.
порою отклоняются от линейной зависимости.
Особое значение необходимо уделить параметру  , поскольку он определяет чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности.
, поскольку он определяет чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности.
В общем случае, если  >1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность
>1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность  . Соответственно, при
. Соответственно, при  < 1 ценная бумага имеет меньший размах отклонений доходности
< 1 ценная бумага имеет меньший размах отклонений доходности  , от средней арифметической (ожидаемой) величины
, от средней арифметической (ожидаемой) величины  , чем рыночная норма отдачи. В этой связи ценные бумаги с коэффициентом
, чем рыночная норма отдачи. В этой связи ценные бумаги с коэффициентом  > 1 классифицируются как более рискованные, чем рынок в целом, а с
> 1 классифицируются как более рискованные, чем рынок в целом, а с  < 1 - менее рискованными.
< 1 - менее рискованными.
Как показывают исследования, для большинства ценных бумаг  > 0, хотя могут встретиться ценные бумаги и с отрицательной величиной
> 0, хотя могут встретиться ценные бумаги и с отрицательной величиной  .
.
Ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле:
 (55)
(55)
где  – вес каждой ценной бумаги в портфеле. Подставим в эту формулу выражение для
– вес каждой ценной бумаги в портфеле. Подставим в эту формулу выражение для  из формулы (54):
из формулы (54):
 (56)
(56)
Для придания этой формуле компактности, Шарп предложил считать рыночный индекс как характеристику условной (n+1)-ой ценной бумаги в портфеле. В таком случае, второе слагаемое уравнения (56) можно представить в виде:
 (57)
(57)
где:  ; (57а)
; (57а)
 .
.
при этом считается, что дисперсия (n+1)-ой ошибки равна дисперсии рыночной доходности:  . Выражение (15а) представляет собойсумму взвешенных величин "беты" (
. Выражение (15а) представляет собойсумму взвешенных величин "беты" ( ) каждой ценной бумаги (где весом служат
) каждой ценной бумаги (где весом служат  и называется портфельной бетой (
и называется портфельной бетой ( ). С учетом выражений (56) и (57) формулу (55) можно записать так:
). С учетом выражений (56) и (57) формулу (55) можно записать так:
 (58)
(58)
а поскольку  , то окончательно имеем:
, то окончательно имеем:
 (59)
(59)
Итак, ожидаемую доходность портфеля  можно представить состоящей из двух частей:
можно представить состоящей из двух частей:
а) суммы взвешенных параметров  каждой ценной бумаги –
каждой ценной бумаги –  …..+
…..+  , что отражает вклад в
, что отражает вклад в  самих ценных бумаг,и
самих ценных бумаг,и
б) компоненты 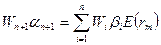 , то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.
, то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.
Дисперсия портфеля в модели Шарпа представляется в виде:
 (60)
(60)
При этом необходимо иметь в виду, что  , то есть
, то есть  , а
, а  . Значит, дисперсию портфеля, содержащего n ценных бумаг, можно представить состоящей из двух компонент:
. Значит, дисперсию портфеля, содержащего n ценных бумаг, можно представить состоящей из двух компонент:
а) средневзвешенных дисперсий ошибок  , где весами служат
, где весами служат  , что отражает долю риска портфеля, связанного с риском самих ценных бумаг (собственный риск);
, что отражает долю риска портфеля, связанного с риском самих ценных бумаг (собственный риск);
б)  - взвешенной величины дисперсии рыночного показателя
- взвешенной величины дисперсии рыночного показателя  , где весом служит квадрат портфельной беты, что отражает долюриска портфеля, определяемого нестабильностью самого рынка (рыночныйриск)
, где весом служит квадрат портфельной беты, что отражает долюриска портфеля, определяемого нестабильностью самого рынка (рыночныйриск)
В модели Шарпа цель инвестора сводится к следующему:
необходимо найти минимальное значение дисперсии портфеля
 (61)
(61)
при следующих начальных условиях:
 (62)
(62)
 (63)
(63)
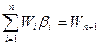 (64)
(64)
Таким образом для построения границы эффективных портфелей в модели Шарпа необходимо выполнить следующие основные этапы:
1. Выбрать n ценных бумаг, из которых формируется портфель, и определить
исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности 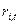 каждой ценной бумаги.
каждой ценной бумаги.
2. По рыночному индексу (например, АК&М) вычислить рыночные доходности  для того же промежутка времени.
для того же промежутка времени.
3. Определить величину дисперсии рыночного показателя  , а также значения ковариаций
, а также значения ковариаций  доходностей каждой ценной бумаги с рыночной
доходностей каждой ценной бумаги с рыночной
нормой отдачи и найти величины  :
:

4. Найти ожидаемые доходности каждой ценной бумаги 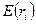 и рыночной
и рыночной
доходности  и вычислить параметр
и вычислить параметр  :
:

5. Вычислить дисперсии  ошибок регрессионной модели
ошибок регрессионной модели
6. Подставить эти значения в соответствующие уравнения
После такой подстановки выяснится, что неизвестными величинами являются веса  ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля
ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля  , можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.
, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.
Дата добавления: 2015-09-03; просмотров: 155 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема Основные положения модели Г. Марковица | | | ВНИМАНИЕ!! Книга содержит шокирующие сцены, сцены с двойным подтекстом, сцены, которые заставляют затаить дыхание, нецензурную лексику, сцены, касающиеся наркотиков и алкоголя. |