Нахождение коэффициентов и построение графика линейного приближения

Величины X и Y могут быть функционально зависимы, но по результатам измерений значений этих величин сложно установить вид фактической зависимости. Метод наименьших квадратов — один из важнейших способов оценки неизвестных величин по результатам измерений, содержащим случайные ошибки и нахождения зависимости между X и Y. Суть метода в том, что условием оценки является минимизация суммы квадратов отклонений выборочных данных от определяемой оценки.

Вычислим сумму квадратов отклонений точек прямой 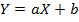от выборочных значений Y:

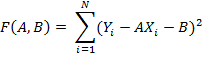
Необходимо взять такие A и B, чтобы F(A,B) достигала своего минимума как функция переменных А и В.

Минимум функции двух переменных должен удовлетворять необходимому и достаточному условию существования минимума. Необходимое условие экстремума функции нескольких переменных — равенство нулю частных производных первого порядка. Получаем систему уравнений:

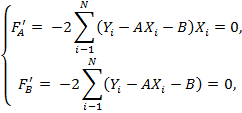
Раскроем скобки и получим следующее:

Где: , , , , 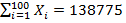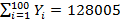N=81. Получим:

Решим эту систему уравнений методом Гауса:

~

Отсюда получаем: A=1,49687975839008; B=-984,25294408128.

Значит уравнение линейной регрессии принимает вид:

Рис. 11

Дата добавления: 2015-09-03