Читайте также:
|
X Y X Y X Y
1793
1388
1723
Теперь вычислим выборочные параметры: выборочные средние 
, выборочные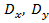 
и исправленные дисперсии 
, исправленные 
и выборочные 
средние квадратические отклонения, центральые 
и начатьные моменты 
, моды 
и медианы 
и найдём выборочный коэффициент корреляции по формуле
А также выразим визуально с помощью полигонов и гистограмм частоты, относительные нормированные частоты и функции распределеня
Выборочные средние значения это приближение теоретического среднего распределения, основанное на выборке из него.
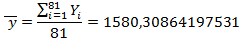
Выборочные дисперсии это оценка теоретической дисперсии распределения на основе выборки.
Исправленные дисперсии:
Средние квадратические отклонения показатель рассеивания значений случайной величины относительно её математического ожидания.
Исправленные cредние квадратические отклонения:
Моменты - числовая характеристика распределения данной случайной величины.
Начальные моменты:
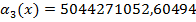
Центральные моменты:
Мода (значение во множестве наблюдений, которое встречается наиболее часто)
Медиана (квантиль 0,5):
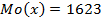
Рассчитываем коэффициент корреляции - показывает статистическую взаимосвязь двух или нескольких случайных величин
Так как 
намного ближе к 1, чем к 0, можно сделать вывод о том, что зависимость между X и Y достаточно тесная.
Дата добавления: 2015-09-03; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка задачи | | | Нахождение коэффициентов и построение графика линейного приближения |