Химическая связь

Окружающие нас разнообразные вещества состоят из атомов, скрепленных, как говорят, химическими связями. Еще более разнообразные химические превращения различных веществ обусловлены разрывом одних и образованием других, как правило, более прочных связей. Принципиально, что только квантовая механика смогла объяснить и количественно определить химическую связь как вид взаимодействия атомов, который обусловлен совместным использованием их электронов.

2.5. Расчет энергии и волновой функции молекулярного иона Н₂⁺ вариационным вариантом метода МО ЛКАО

Основанная на квантовых законах теория простейшей молекулы Н₂⁺ служит исходным пунктом для теории химической связи более сложных молекул, в той же степени, как теория водородоподобных атомов – для теории многоэлектронных атомов.

е r1 R r2

Молекулярная орбиталь (МО) электрона e в поле двух протонов 1 и 2, находящихся на расстоянии R, представляется в виде линейной комбинации атомных орбиталей (ЛКАО): (2.5) где - орбитали атомов водорода в основном 1 s состоянии; a 0 – радиус первой орбиты Бора.

Искомые “весовые“ коэффициенты c ₁ и c ₂согласно вариационномуметоду находятся из условия минимума энергии системы

(2.6)

где 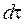- элемент объема, по которому производится интегрирование, знак комплексного сопряжения (*) для действительных функций может быть опущен. Оператор Гамильтона для молекулярного иона имеет вид:

. (2.6’)

Алгебраически преобразуя числитель и знаменатель (2.6), получаем

(2.7)

где (2.7’) . (2.7”)

Необходимые условия минимума энергии после выполнения соответствующих математических действий приводят к однородной системе двух линейных уравнений:

(2.8)

Для совместности уравнений необходимо, чтобы “вековой” определитель системы был равен нулю.

. (2.9)

Вторая в строке (2.9) - сокращенная запись обобщающего определителя n -го порядка принципиально определяет решение для волновой функции из n атомных орбиталей.

Для нормированных 1 s -орбиталей а единственный интеграл их перекрывания (см. (2.7”)).

Входящие в (2.9) энергетические матричные элементы (2.7’) получили название кулоновского интеграла: . С учетом (2.6’) он включает атомную составляющую (-1/2), энергию взаимодействия электрона со вторым протоном и кулоновское отталкивание ядер. Два оставшихся матричных элемента (2.7’) назвали обменным интегралом, именно он фактически и определяет энергию химической связи (см. ниже).

Определитель (2.9) и вытекающее из него квадратное уравнение имеет два решения

Подстановка этих энергий в (2.8) для определения с ₁ и с ₂ дают соответственно симметричную и антисимметричную (*) молекулярные орбитали:

Рис. 2.3. Потенциальные кривые и энергетические уровни связывающего и отталквательного состояния Н2^+ (а). Энергетические уровни без учета интеграла перекрывания (б).
	Рис. 2.4. Схема и заселенности МО молекул и радикалов, образованных атомами элементов 1-го периода.

Рис. 2.5. Схематическое изображение образования связывающей σ1 s и разрыхляющей σ*1 s МО.

Основные следствия:

1. Знаки исходных АО имеют смысл только в процедуре образования МО. Переход от области “+“ к области “-“ в разрыхляющей антисимметричной МО соответствует т.н. узловой точке с нулевой вероятностью нахождения электрона между ядрами. Для определяющей химическую связь симметричной МО характерно увеличение электронной плотности между ядрами.

2. Расположение энергетических уровней (2.9) и (2.9*) на рис. 2.3 показывают, что электрон на разрыхляющей орбитали разрыхляет связь сильнее, чем укрепляет ее электрон на связывающей.

3.Энергия диссоциации молекулы при разрыве химической связи преимущественно определяется обменным интегралом

---

Дата добавления: 2015-09-02