Постановка задачі

Вивчення та аналіз діяльності підрозділів ОВС України вимагає проведення досліджень в часі. Основною складовою таких досліджень є побудова та аналіз часових рядів для тих чи інших статистичних показників.

Часовим рядом називається перелік числових значень деякого статистичного показника в послідовні моменти або періоди часу. Часові ряди зазвичай зображають графічно або задають у вигляді таблиць.

При вивченні часових рядів основною метою є прогнозування відповідних явищ в майбутньому. Для цього розв’язують одну із найважливіших задач дослідження часових рядів – виявлення головної тенденції зміни значень показника.

Типовим прикладом часового ряду є наведена таблиця, яка показує зміни загальної кількості зареєстрованих та розкритих злочинів (за їх видами) з року в рік у деякому підрозділі.

Рік
Зареєстровано
Розкрито

Значення показника будь-якого часового ряду є результатом взаємодії найрізноманітніших причин, одні з яких можуть діяти постійно і тривалий час, інші – діяти іноді і короткий час. Ті причини, що діють постійно і тривалий час, є головними і визначають тенденцію змін. Ті причини, що діють іноді і короткочасно, є випадковими і затемнюють тенденцію змін. Отже, для вироблення правильних висновків про закономірності змін того чи іншого показника необхідно виділити головну тенденцію, відокремивши її від коливань, викликаних випадковими причинами.

Таким чином, у загальному випадку значення показника часового ряду, який нас цікавить, в кожний момент часу t може бути представлене у вигляді суми значень невипадкової та випадкової функцій, кожна з яких залежить від часу.

Невипадкова функція, яка характеризує детерміновану (визначену, обумовлену) складову часового ряду, називається трендом. Тренд відображує вплив на значення показника часового ряду деяких постійно діючих факторів, специфічних для кожного явища.

Випадкова функція, яка відображує відхилення від тренда за рахунок дії неконтрольованих випадкових факторів, називається випадковою компонентою.

Задачею виявлення тренду називається задача підбору аналітичного виразу (формули), яка описує даний часовий ряд, осереднюючи поточні значення його статистичного показника.

Особливості цієї задачі такі:

q отримані статистичні дані завжди містять в собі випадкові коливання;

q через ці коливання недоцільно підбирати формулу, графік якої точно співпадає зі статистичними даними;

q достатньо підібрати таку формулу, графік якої є близьким до значень статистичного показника часового ряду.

Емпіричною формулою називається досить простий аналітичний вираз, значення якого найбільш близькі до значень статистичного показника часового ряду.

Процес побудови емпіричної формули складається з двох етапів:

q вибір виду емпіричної формули;

q визначення найкращих значень параметрів цієї формули.

Припустимо, що вид емпіричної формули вибрано. Тоді найкращі числові значення параметрів вибраної емпіричної формули визначають так, щоб її графік проходив якнайближче до значень даного часового ряду. При цьому якнайближчим вважається такий графік, для якого сума квадратів відхилень значень часового ряду від розрахункових є мінімальною. Відповідний метод називається методом найменших квадратів.

В MS Excel за допомогою методу найменших квадратів є можливість будувати емпіричні формули двох видів: лінійну залежність 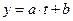і показникову залежність .

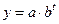Для цього використовуються такі формули:

1) «=ИНДЕКС(ЛИНЕЙН(Y;T);1)» – дає значення параметра a лінійної залежності;

2) «=ИНДЕКС(ЛИНЕЙН(Y;T);2)» – дає значення параметра b лінійної залежності;

3) «=ИНДЕКС(ЛГРФПРИБЛ(Y;T);1)» – дає значення параметра b показникової залежності;

4) «=ИНДЕКС(ЛГРФПРИБЛ(Y;T);2)» – дає значення параметра a показникової залежності.

Тут Y – діапазон комірок, який містить значення показника часового ряду, T – діапазон комірок, який містить моменти часу.

Дата добавления: 2015-08-21