Задача 2.5

По известным координатам вершин треугольника , , записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла .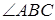

Решение: Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула (2.4), от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).

1. Найдем уравнение стороны . В качестве точки прямой можно взять точку с заданными координатами, а в качестве направляющего вектора – вектор . Найдем координаты вектора :

2. Тогда каноническое уравнение стороны запишется как: , или .

3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны 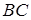: координаты вектора .

4. Откуда каноническое уравнение: 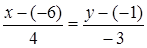. Следовательно, общее уравнение: .

5. Для стороны : координаты направляющего вектора .

6. Каноническое уравнение: 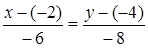, или .

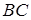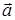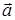7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах и треугольника отложить орты (соответственно и ) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов и ).

8. Для нахождения орта 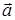необходимо знать координаты вектора :

, откуда 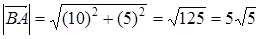и, соответственно 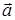определится как:

(Рис. 2.5).

Рис. 2.5. Иллюстрация решения задачи 2.5

9. Аналогично определим орт :

; ;

. Теперь определим их сумму:

.

10. Тогда каноническое уравнение биссектрисы:

.

Ответ: .

Дата добавления: 2015-08-21