Читайте также:
|
Составить уравнение прямой, проходящей через точку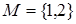 
параллельно прямой 
.
Решение: Так как искомая прямая по условию задачи должна быть параллельной исходной, это значит, что они имеют один угол наклона к оси 
. Угол наклона исходной прямой можно определить из формулы (2.6): 
. Исходная прямая задана в общей форме, следовательно для нее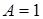 
; 
; подставляя значения коэффициентов исходной прямой, находим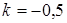 
. Обозначим координаты точки 
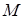как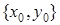 
, имеем 
, 
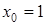; прямую, проходящую через эту точку, можно описать уравнением с угловым коэффициентом (2.7); подставим в него известные значения, получим: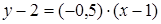 
. Проведя несложные преобразования, получим искомое уравнение: 
.
Замечание: можно было провести и другие рассуждения:
1. Прямые должны быть параллельны, это значит, первые два коэффициента в уравнении у них должны быть одинаковы (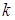
– имеет одно значение), следовательно, нужно найти только значение свободного члена 
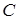; по определению 
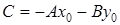, где 
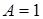– известны из исходного уравнения: ; , а 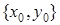– координаты начального радиус-вектора.
2. Нормаль у параллельных прямых – общая, значит, начальный радиус-вектор можно провести через заданную точку :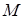 
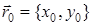; подставив ее координаты в выражение для 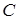, получаем: 
.
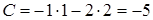3. Подставляем в искомое уравнение, получаем искомое уравнение.
Ответ: .
Дата добавления: 2015-08-21; просмотров: 34 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 1.4 | | | Задача 2.5 |