Читайте также:
|
Примеры решения типовых задач: векторная алгебра
Задача 1.1.
Даны два вектора 
и 
. Найти координаты вектора 
.
Решение: Из свойства 1 следует, что 
, следовательно: 
.
Ответ: 
.
Задача 1.2
Найти координаты вектора 
, соединяющего точку 
с координатами 
и точку 
с координатами 
.
Решение: Обозначим координаты точки как 
, координаты точки как 
. Из свойства 2 следует: вектор 
имеет координаты 
. Подставляем исходные значения: 
.
Ответ: 
.
Задача 1.3
Доказать, что два вектора 
и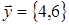 
коллинеарны.
Решение: Из свойства 3 следует, что для решения необходимо проверить выполнение равенства: 
. Подставим заданные значения координат: 
, откуда: 
. Равенство верно.
Ответ: исходные вектора коллинеарны.
Задача 1.4
Задан вектор 
и известно, что точка имеет координаты 
. Найти координаты точки – начала вектора.
Решение: Введем обозначения: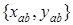 
– координаты вектора 
, 
– координаты точки , 
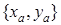– координаты точки .
1. Из свойства 2 следует, что для решения необходимо решить два уравнения: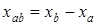 
; 
.
2. Подставим известные величины: 
; 
; откуда искомые координаты: 
; 
. Ответ: точка имеет координаты 
.
Дата добавления: 2015-08-21; просмотров: 31 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Предлоги | | | Задача 2.2 |