Читайте также:
|
Записать уравнение плоскости, проходящей через точки 
, 
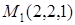и образующей с плоскостью 
угол равный 
.
Решение: 1)Для определенности положим, что 
– фиксированная точка, радиус-вектор которой 
; 
– точка, с помощью которой строим вектор 
, лежащий в искомой плоскости. Его координаты: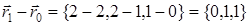 
.
2) Так как нормаль 
искомой плоскости перпендикулярна этому вектору 
, то 
. Скалярное произведение в декартовой системе координат определяется по формуле: 
, откуда получаем уравнение 
3) Нормаль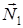 
плоскости имеет координаты 
. Подставим известные значения в формулу (2.4):
,
или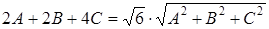 
.
1. Итак, имеем систему из двух уравнений относительно трех неизвестных: 
.
2. Уменьшим число неизвестных, для чего разделим обе части на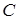 
:
,
3. Подставим выражение из первого уравнения во второе, получим:
, откуда 
.
4. Получили пропорцию коэффициентов нормали: 
, откуда в качестве координат нормали возьмем 
.
5. Уравнение плоскости запишется в виде:
. Ответ: 
.
Дата добавления: 2015-08-21; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 2.5 | | | Все товары имеют необходимые сертификаты. |