Расчет цепи методом узловых напряжений

Пункты 2.1... 2.3 полностью совпадают с пунктами 1.1... 1.3 соответственно рассмотренного выше алгоритма. Поэтому нумерацию пунктов данного алгоритма начнем с пункта 2.4.

2.4 Обозначение узловых напряжений

Обозначим узлы, например, так, как показано на рисунке 2. В качестве опорного выберем узел С, памятуя о том, что таковым может быть любой узел. Напряжение узлов А и В относительно опорного обозначим 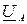и 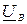соответственно.

2.5 Запись исходной системы узловых уравнений в общем виде

Где:

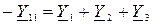- собственная проводимость узла А

- взаимная проводимость узлов А и В

- собственная проводимость узла В

2.6 Расчет проводимостей

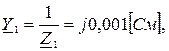
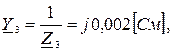
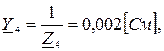
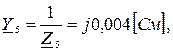
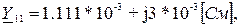
2.7 Расчет узловых напряжений

Так же, как и в предыдущем случае используем метод Крамера.

Определитель системы равен:

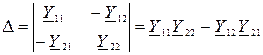
Подставляя значения получим:

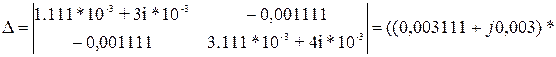
Подставляя значения получим:

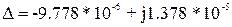
Определитель для напряжения :

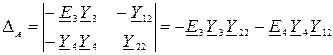
Подставляя значения получим:

После подстановки получим:

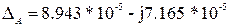
Следовательно, узловое напряжение равно:

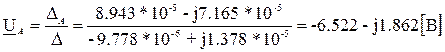
Определитель для напряжения :

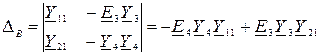
Подставляя значения получим:

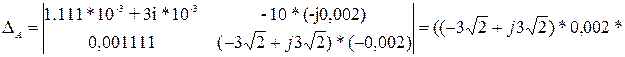
После подстановки получим:

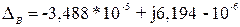
Следовательно, узловое напряжение равно:

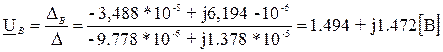
Поскольку 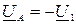и , что соответствует обозначениям рисунка 2 и решению по методу контурных токов (п. 1.9), то в данной задаче ограничимся нахождением узловых напряжений и не будем рассчитывать остальные величины.

Дата добавления: 2015-08-21