
Читайте также:
|
ВВЕДЕНИЕ
Целью курсовой работы является закрепление теоретического материала по темам ‹‹Анализ линейных цепей с постоянными параметрами при гармоническом воздействии›› и ‹‹Методы анализа сложных цепей››, а так же усвоение методики и приобретение практических навыков расчета сложных электрических цепей.
Для успешного выполнения используется следующий теоретический материал:
- способы представления гармонических электрических величин и метод комплексных амплитуд;
- законы Ома и Кирхгофа в комплексной форме;
- сущность методов контурных токов и узловых напряжений расчета линейных электрических цепей;
- методы решения системы линейных алгебраических уравнений, в том числе и с комплексными коэффициентами.
Расчет методом контурных токов
1.1 Изображение расчетной схемы замещения электрической цепи для выбранного варианта
Пусть в первой, третьей и пятой ветвях содержатся емкости, а во второй и четвертой – сопротивления.
Тогда расчетная схема замещения цепи будет иметь вид, изображенный на рисунке 1.

Рисунок 1 – Расчетная схема замещения электрической цепи
1.2 Изображение комплексной схемы замещения
Комплексная схема замещения цепи изображена на рисунке 2.

Рисунок 2 – Комплексная схема замещения электрической цепи
Цепь имеет три узла (А,В,С) и пять ветвей. Следовательно, при использовании метода уравнений Кирхгофа необходимо решать систему из семи уравнений.
Метод контурных токов позволяет решать систему из трех уравнений, так как в цепи три независимых контура.
1.3 Выбор положительных направлений токов в ветвях
Условные положительные направления токов в ветвях выбираются произвольно. Выберем их так, как указано на рисунке 2.
1.4 Выбор направления обхода и обозначение независимых контуров
Контурные токи обозначим также произвольно, например, по часовой стрелке, как на рисунке 2. Положительные направления обхода контуров выберем совпадающими с направлениями контурных токов.
1.5 Запись системы контурных уравнений для расчета контурных токов в общем виде
Составим систему контурных уравнений для контурных токов в общем виде:



Где:
 - комплексные контурные токи;
- комплексные контурные токи;
 - комплексные ЭДС;
- комплексные ЭДС;
 - собственные комплексные сопротивления контуров;
- собственные комплексные сопротивления контуров;
 - взаимные комплексные сопротивления контуров.
- взаимные комплексные сопротивления контуров.
Здесь:






1.6 Расчет сопротивлений элементов схемы на указанной частоте





1.7 Расчет собственных и взаимных сопротивлений





1.8 Расчет контурных токов
Систему уравнений будем решать методом Крамера. Найдем сначала определитель системы:

Подставляя значения получим:

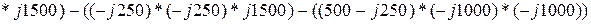
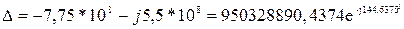
Определитель для тока  :
:

После подстановки значений имеем:



Разделив  на
на  , получим значение контурного тока
, получим значение контурного тока  :
:


Определитель для тока  :
:
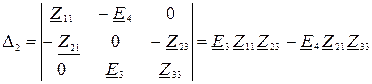
После подстановки имеем:
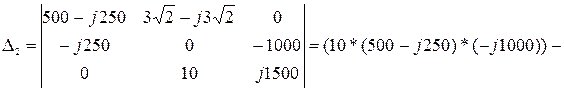


Разделив  на
на  , получим значение контурного тока
, получим значение контурного тока  :
:


Определитель для тока  :
:
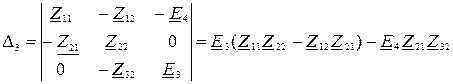
После подстановки имеем:



Разделив  на
на  , получим значение контурного тока
, получим значение контурного тока  :
:


1.9 Расчет токов в ветвях и напряжений на элементах
В соответствии с обозначениями рисунка 2 получаем:










1.10 Проверка правильности решения задачи на основе выполнения законов Кирхгофа
Проверим выполнение 1 закона Кирхгофа.
Для узла А:

Для узла В:

Следовательно, первый закон Кирхгофа выполняется.
Проверим выполнение 2 закона Кирхгофа.
Для контура 1:



Таким образом, можно утверждать, что задача решена верно, поскольку законы Кирхгофа Выполняются.
1.11 Запись результатов в виде мгновенных значений










Дата добавления: 2015-08-21; просмотров: 177 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пропозиції щодо оформлення | | | Расчет цепи методом узловых напряжений |