
Читайте также:
|
В начале необходимо задать свойства Scope 2 на вкладе Data History задать переменную Variable name. Пусть Variable name = imp (рисунок 4).

Рис 4. Свойства блока Scope 2
Задаем значение времени, в течение которого будет производиться моделирование Simulation stop time = 50.
Запускаем модель. Это нужно для определения импульсной характеристики первичного преобразователя. Она будет находиться в переменной imp.signals.values.
Форма сигнала, получаемого после блока дискретного дифференциатора Discrete Derivative, изображена на рисунке 5.

Рис 5. Форма сигнала после блока дискретного дифферениатора
Считаем прямое преобразование Фурье. В командной строке MATLAB необходимо ввести:
>> Y=fft(imp.signals.values)
Строим АЧХ первичного преобразователя командой:
>> plot(abs(Y))
Полученная АЧХ приведена на рисунке 6.

Рис 6. АЧХ первичного преобразователя
Находим частотную характеристику корректирующего звена, как обратную к полученной характеристике Y командой поэлементного деления:
>> Z=1./Y
Строим АЧХ корректирующего звена:
>> plot(abs(Z))
Полученная АЧХ изображена на рисунке 7.

Рис 7. АЧХ корректирующего звена
Считаем обратное преобразование Фурье и получаем импульсную характеристику звена:
>> S=ifft(Z)
Полученные значения – это и есть коэффициенты фильтра.
Для построения скорректированного сигнала в блоке цифрового фильтра Discrete Filter необходимо установить параметр Numerator = S’.
Далее необходимо запустить моделирование системы, предварительно установив значение времени, в течении которого будет производиться моделирование Simulation stop time = 50.
Форма скорректированного сигнала, получаемого после блока дискретного фильтра, изображена на рисунке 8.
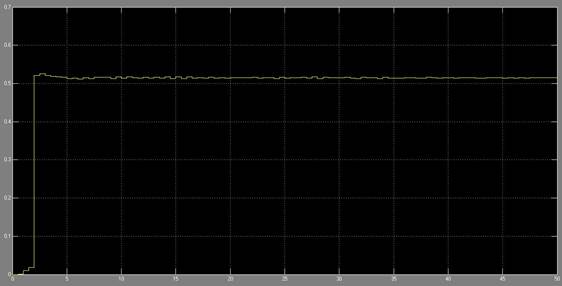
Рис 8. Форма скорректированного сигнала
Заключение
В настоящей курсовой работе была построена система цифровой коррекции сигнала, подающегося на блок, содержащий помеху.
Данная система была разработана с использованием компьютерной среды моделирования MATLAB Simulink.
Из полученного изображения формы скорректированного сигнала видно, что цифровой фильтр не позволил окончательно убрать помеху, заданную в блоке wn. Это связано с тем, что блок дополнительно содержит так называемый «белый» шум, который создает помеху на частоте полезного сигнала. Для фильтрации подобных шумов необходимо построение намного более сложных систем.
Дата добавления: 2015-08-21; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Построение системы цифровой коррекции | | | Аннемария Штилер |