Игровые формы занятий по математике.

Игра как форма внеклассной работы по математике предполагает командные, групповые или индивидуальные соревнования учащихся по решению математических задач.

Признаки, характеризующие игру:

· Наличие объекта игры;

· Наличие правил общения в условиях соревнования;

· Наличие общей цели игрового коллектива;

· Динамизм ситуации;

· Ограниченность игрового времени и его распределение по этапам игры;

· Объективность оценки результатов;

· Четкая система организации, планирования и стимулирования игры;

· Занимательная формулировка заданий, задач.

Математическая игра «Морской бой» (6 класс)

Основные характеристики игры:

1. Цели:

Образовательные: повторение и закрепление материала по темам: делимость чисел, действия с обыкновенными дробями с разными знаменателями, положительные и отрицательные числа, сложение и вычитание положительных и отрицательных чисел

Развивающие: самостоятельность мышления, развитие смекалки

Воспитательные: умение работать в команде

Игровые: набрать наибольшее количество баллов

2. Объект:

Темы 6 класса (море)

3. Роли: две команды по 4-5 моряков (учащихся) во главе с капитанами, наблюдатели (по одному на команду), жюри (учащиеся с очень хорошей успеваемостью), болельщики (оставшиеся ученики)

4. Правила: На доске нарисованы 2 поля 10х10 клеток (как в игре «Морской бой»). На листочках у каждой команды нарисовано поле, на котором они расставляют свои корабли (4 – однопалубных, 3 – двухпалубных, 2 – трехпалубных, 1 – четырехпалубный; правило расположения кораблей аналогично соответствующей игре). Каждому кораблю соответствует своя тема и уровень сложности.

Далее проводится конкурс капитанов, который определяет, какая из команд стреляет первой. Команда капитана-победителя начинает стрелять.

· Если удар «мимо» (пустая клетка), то право хода переходит к другой команде.

· Если попадают, то должны решить задание (чтобы получить снаряд и выстрелить).

· Если задание не решено, то право хода передается другой команде, однако, в следующий раз команда может стрелять в тоже место.

· Если команда не смогла решить задание, оно может быть решено другой командой.

На решение одного задания даются не более чем две минуты.

Морская битва длится 45 минут. За 5 минут до конца игры каждая команда подводит итоги (количество сбитых кораблей).

Жюри

Оценивают результаты по системе оценки (см. таблицу).

Наблюдатели

На каждом корабле находится наблюдатель, который напоминает правила игры, помогает разобраться в задании.

Болельщики

Придумывают кричалки, которые оцениваются жюри

5. Реквизит: два листа с нарисованными полями 10х10 клеток (как в игре «Морской бой»); карточки с заданиями; два корабля для команд (рисунки кораблей); две шляпы для капитанов; правила игры для команд, с таблицей оценивания.

6. Время: 45 минут

7. Система оценки результатов:

Сбитые корабли оцениваются в баллах, как

1 однопалубный	1 очко
1 двухпалубный	2 очка
1 трехпалубный	3 очка
1 четырехпалубный	4 очка
Если к концу игры корабль сбит не полностью, то присуждается количество очков, соответствующее количеству сбитых клеток. За несоблюдение правил вычитается 1 очко. За решение задачи другой команды присуждается одно очко.

8. Ход игры:

Здравствуйте, сегодня мы с вами перенесемся в захватывающий мир приключений. На нашем импровизированном море сойдутся в нешуточной битве два корабля, которые мы поприветствуем. Итак, домашним заданием у вас было придумать название команды, девиз и выбрать капитана.

Зачитываются правила и система оценивания. Они также выдаются каждой команде на листочках.

Приветствие команд. Представление капитанов.

Конкурс капитанов.

Вычислить:

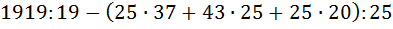
Вычислить:

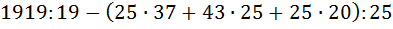
Решение:

= =

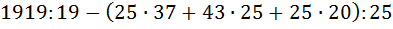Морской бой.

Задания для однопалубных кораблей по теме: Делимость чисел.

Сформулируйте признак делимости на 3.	Какие из чисел делятся на 3? 75 432, 2 772 825, 5 402 071
Сколько здесь простых чисел? 1, 8, 5, 11, 10, 15, 19, 6, 2, 13, 25, 4, 17	Сколько здесь составных чисел? 1, 8, 5, 11, 10, 15, 19, 6, 2, 13, 25, 4, 17
Верно ли, что все простые числа – нечетные?	Верно ли, что если число делится на 3, то оно делится и на 9?
Найдите наибольший общий делитель чисел 675 и 825.	Найдите наибольший общий делитель чисел 630 и 252.
Найти наименьшее общее кратное чисел 72 и 99.	Найти наименьшее общее кратное чисел 45 и 135.
Сколько нечетных цифр вы знаете?	Сколько четных цифр вы знаете?

Ответы:

Если сумма цифр числа делится на 3, то и число делится на 3.	75 432, 2 772 825
7 (1, 5, 11, 19, 13, 2, 17)	6 (8, 10, 15, 6, 25, 4)
Нет, например число 2 является простым и четным.	Нет, например число 15.
(675, 825) = 75	(630, 252) = 126

Задания для двухпалубных кораблей по теме: Сложение, вычитание, умножение и деление обыкновенных дробей с разными знаменателями.

Сформулируйте правило сложения обыкновенных дробей с разными знаменателями.	Сформулируйте правило вычитания обыкновенных дробей с разными знаменателями.
Вычислить:	Вычислить:
Решить уравнение:	Решить уравнение:
Упростите и найдите значение выражения:	Упростите и найдите значение выражения:
Выполните действие:	Выполните действие:
Сформулируйте правило деления обыкновенных дробей.	Сформулируйте правило умножения обыкновенных дробей.
Выполните действия:	Выполните действия:
Найдите площадь прямоугольника, если известно, что стороны равны: a=4 , b= .	Найдите сторону a прямоугольника, если известно, что площадь его равна 15, а сторона b=7 .

Ответы:

Чтобы сложить дроби с разными знаменателями, нужно: 1. Привести дроби к общему знаменателю 2. Применить правило сложения дробей с одинаковыми знаменателями	Чтобы вычесть дроби с разными знаменателями, нужно: 1. Привести дроби к общему знаменателю 2. Применить правило вычитания дробей с одинаковыми знаменателями
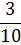
x=2	y=1
s w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:num><m:den><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>2</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">	s w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:num><m:den><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>5</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
1. Умножить числители двух дробей 2. Умножить знаменатели двух дробей 3. Первое произведение записать в числитель, а второе в знаменатель.	Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
S=1	a=2

Задания для трехпалубных кораблей на тему: Положительные и отрицательные числа.

Что называется координатной прямой?	Что называется координатой точки?
Какие числа называют противоположными?	Какие числа называют целыми?
Как найти модуль отрицательного числа?	Что такое модуль числа А?
Найти значение выражения:	Найти значение выражения:
Какие числа можно написать вместо *, чтобы получилось верное равенство? -5*83>-5183	Какие числа можно написать вместо *, чтобы получилось верное равенство?
Поставьте вместо * знак < или >, чтобы получилось верное неравенство:	Поставьте вместо * знак < или >, чтобы получилось верное неравенство:
Найдите значение:	Найдите значение:
Выберите то число, у которого модуль больше:	Выберите то число, у которого модуль больше:

Ответы:

Прямая, с выбранными на ней началом отсчета, единичным отрезком и направлением.	Число, показывающее положение точки на прямой.
Два числа, отличающиеся друг от друга только знаками.	Натуральные числа, противоположные им и ноль.
Равен противоположному числу.	Расстояние от начала координат до точки А.
12,4
	5,4,3,2,1,0
<	>
56,5	107,3
s w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:num><m:den><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>7</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

Задания для четырёхпалубных кораблей на тему: Сложение и вычитание положительных и отрицательных чисел.

Как ведет себя число от прибавления к нему положительного числа?	Как ведет себя число от прибавления к нему отрицательного числа?
Как сложить два отрицательных числа?	Как сложить два числа с разными знаками?
Вычислить:	Вычислить:
За день температура воздуха изменилась на -12 градусов и к вечеру стала равна -8 градусов. Какой была температура утром?	Температура воздуха утром была 5 градусов, а к вечеру она стала равна -2 градуса. На сколько градусов изменилась температура за день?
Найдите значение выражения:	Найдите значение выражения:
Найдите расстояние между точками: М(2,3) и N(-4,2)	Найдите расстояние между точками: P() и K(

Ответы:

увеличивается	уменьшается
Сложить их модули, поставить перед полученным числом знак «-».	Из большего модуля слагаемых вычесть меньший, поставить перед полученным числом знак того слагаемого, модуль которого больше.
4 градуса	На -7 градусов
6,5

Подведение итогов. Награждение участников.

Список литературы.

1. Антонович Н.К. 100 математических игр для учащихся 5-8 классов. – Новосибирск, 1963.

2. Аренс В. Математические игры и развлечения. – СПб.: Физика, 1911.

3. Баше К. Игры и задачи, основанные на математике. – СПб. – М.: Издание М.О.Вольфа, 1877.

4. Весёлый час: Игры, задачи, головоломки, фокусы, юмор, занимательная смесь/Сост. Н.Тужилин. – Симферополь: Крымиздат, 1964.

5. Гик Е.Я. Занимательные математические игры. – М.: Знание, 1987.

6. Доморяд А.П. Математичекие игры и развлечения. – М.: Физматгиз. 1961.

7. Игнатьев Е.И. Математические игры, развлечения и задачи. – СПб.: 1904.

8. КВН// Математика в школе. – 1988. - №6.

9. Коваленко В.Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990.

10. Математические соревнования. Арифметика и алгебра. – М.: Наука. – 1970.

11. Соболевский Р.Ф. Логические и математические игры. – Минск: Народная асвета, 1977.

Дата добавления: 2015-09-03