Случайные процессы считаются стационарными в широком смысле или слабо стационарными.

Процесс, стационарный в узком смысле, стационарен и в широком смысле, но не наоборот.

ЭРГОДИЧЕСКИЕ ПРОЦЕССЫ

· Статистическую обработку ансамбля реализаций по множеству можно заменить длительным наблюдением за одной реализацией с усреднением по времени значений x на интервале Т через промежуток D t. В этом случае число замеров будет n = T/ D t и

.

Тогда среднее по времени случайного процесса при длительном наблюдении (T® ¥) и при Dt®0 находится как

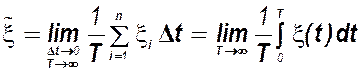
Если любая реализация стационарных случайных процессов достаточно полно представляет статистические свойства процесса в целом, то средние по множеству (по ансамблю реализаций) и средние по времени характеристики совпадают. Стационарные случайные процессы, для которых числовые характеристики, усреднённые по ансамблю и по времени, эквивалентны, называются эргодическими.

· Если эргодичность случайного процесса установлена с учётом критериев согласия (независимость потребителей энергии, отсутствие очень мощных потребителей энергии, асимптотическое свойство автокорреляционной функции, отсутствие периодических составляющих с бесконечной продолжительностью и др.) статистический анализ одной реализации позволяет сравнительно просто получить числовые характеристики случайного процесса, усредненные по времени:

- математическое ожидание , которое является средним значением случайного процесса и представляет его постоянную составляющую;

- среднее квадрата x _ср² = _ср² = - определяет среднюю мощность случайного процесса;

- дисперсию , численно равную средней мощности флуктуаций (переменной составляющей) случайного процесса (s_x - эффективное значение переменной составляющей процесса);

Дата добавления: 2015-09-03