Читайте также:
|
«Теория вероятностей и математическая статистика»
| № п/п | Название разделов, тем | |
| ТЕОРИЯ ВЕРОЯТНОСТЕЙ | ||
| 1.1 | Введение в теорию вероятностей и математическую статистику. Элементы комбинаторики. | |
| 1.2 | Случайные события | |
| 1.2.1 | Случайные события и действия над ними. Теоретико-множественная интерпретация операций над событиями. | |
| 1.2.2 | Методы определения вероятностей событий (статистическое, классическое, геометрическое и аксиоматическое). Свойства вероятностей. | |
| 1.2.3 | Основные формулы теории вероятностей (правило умножения вероятностей, вероятность появления хотя бы одного события, формулы полной вероятности и Байеса). | |
| 1.2.4 | Схема независимых испытаний Бернулли. Приближенные формулы в схеме Бернулли. | |
| 1.3 | Случайные величины | |
| 1.3.1 | Случайные величины (дискретные и непрерывные), их законы распределения. Числовые характеристики случайных величин. | |
| 1.3.2 | Основные законы распределения дискретных случайных величин (биномиальный, Пуассона, геометрический, гипергеометрический). | |
| 1.3.3 | Основные законы распределения непрерывных случайных величин (равномерный, показательный, нормальный, логнормальный, распределения Пирсона, Стьюдента и Фишера). | |
| 1.3.4 | Предельные теоремы теории вероятностей: закон больших чисел и центральная предельная теорема. | |
| 1.4 | Системы случайных величин | |
| 1.4.1 | Понятие о системе случайных величин. Законы распределения системы. | |
| 1.4.2 | Система двух случайных величин: дискретных и непрерывных. | |
| 1.4.3 | Основные числовые характеристики системы двух случайных величин. | |
| 1.5 | Функция одной случайной величины | |
| МАТЕМАТИЧЕСКАЯ СТАТИСТИКА | ||
| 2.1 | Выборочный метод в статистике. Выборочные характеристики | |
| 2.2 | Статистическое оценивание параметров | |
| 2.2.1 | Точечные оценки параметров распределения и их свойства. | |
| 2.2.2 | Методы получения точечных оценок (моментов, максимального правдоподобия, наименьших квадратов). | |
| 2.2.3 | Интервальные оценки параметров распределения. Нахождение доверительных интервалов для неизвестного признака (математического ожидания, дисперсии или доли признака) в генеральной совокупности. | |
| 2.3 | Проверка статистических гипотез | |
| 2.3.1 | Статистическая гипотеза и общая схема ее проверки. | |
| 2.3.2 | Проверка параметрических гипотез (о математических ожиданиях, дисрперсиях, доле признака в генеральной совокупности, значимости коэффициента корреляции). | |
| 2.3.3 | Проверка непараметрических гипотез. Критерий Пирсона | |
| 2.4 | Корреляционно-регрессионный анализ | |
| 2.5 | Дисперсионный анализ |
При подготовке к экзамену можно воспользоваться книгами из приведенного ниже списка.
Литература
Вариант решения типовых задач
1. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наугад деталей 4 стандартных.
Решение. Воспользуемся классическим определением вероятности:
Определение. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов:
,
где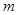 
‑ число элементарных исходов, благоприятствующих наступлению события А; 
‑ число всех равновозможных элементарных исходов испытания.
Вероятность любого события удовлетворяет неравенству 
.
Основное событие А – «среди 6 взятых деталей 4 стандартных». По классическому определению вероятности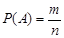 
. Общее число равновозможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов 
. Четыре стандартные детали из семи стандартных можно взять 
способами, при этом остальные 6 – 4 = 2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 – 7 = 3 нестандартных деталей можно 
способами. Следовательно, число благоприятствующих исходов равно 
.
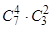2. В трех ящиках находятся одинаковые детали. В 1-ом – 10 деталей, из них 3 нестандартных, во 2-ом –15 деталей, из них 5 нестандартных, в 3-ем – 20 деталей, из них 6 нестандартных. Из наудачу выбранного ящика извлечена деталь.
1) Найти вероятность, что эта деталь оказалась нестандартной.
2) Извлеченная деталь оказалась нестандартной. Найти вероятность того, что деталь извлечена из 2-го ящика.
Решение. Для ответа на первый вопрос воспользуемся формулой полной вероятности.
Пусть событие А может наступить при условии появления одного из несовместных событий 
, 
, … 
, образующих полную группу. Будем эти события называть гипотезами. Вероятность события А в этом случае вычисляется по формуле
,
которая носит название формулы полной вероятности. Здесь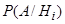 
‑условная вероятность события А при условии, что произошло событие 
.
Замечание. Говорят, что события образуют полную группу, если в результате опыта появится хотя бы одно из них, т.е. появление хотя бы одного события из полной группы есть достоверное событие. Если события, образующие полную группу, попарно несовместны, то в результате опыта появится одно и только одно из этих событий. Для событий полной группы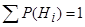 
.
Для ответа на второй вопрос задачи используем формулу Байеса.
Пусть событие А может наступить при условии появления одного из несовместных событий , , …, , образующих полную группу. Вероятности этих гипотез до опыта известны и равны соответственно 
, 
, … 
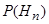. Произведен опыт, в результате которого наступило событие А. Вероятность 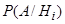гипотезы , после того, как событие А наступило, определяется по формуле Байеса
, 
.
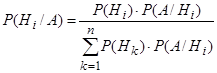1) Обозначим основное событие А – «извлечена нестандартная деталь». Можно сделать три предположения(гипотезы):
‑«деталь извлечена из 1-го ящика»,
‑ «деталь извлечена из 2-го ящика»,
‑«деталь извлечена из 3-го ящика».
Поскольку ящик выбирают случайно, то гипотезы равновозможные, следовательно,
Для нахождения условных вероятностей события А используем классическое определение вероятности. В первой урне из 10 три нестандартные детали, значит, 
. Во второй урне из 15 пять нестандартных деталей, значит, 
В третьей урне из 20 шесть нестандартных деталей, значит,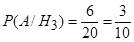 
. По формуле полной вероятности:
.
2) по формуле Байеса найдем 
:
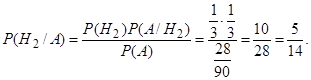
3. Вероятность изготовления на станке детали высшего качества равна 0,8. Найти вероятность того, что из 6 взятых наудачу деталей 4 высшего качества.
Решение. Поскольку речь идет о идет о повторении независимых испытаний, воспользуемся формулой Бернулли. Если в каждом из независимых испытаний вероятность появления события А постоянна и равна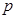 
, то вероятность того, что в 
независимых испытаниях событие А наступит ровно 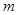раз, определяется по формуле Бернулли
, где 
.
На практике формулой Бернулли удобно пользоваться, если не очень велико. Из условия задачи имеем, что n = 6, m = 4, p = 0,8, q = 1-0,8 = 0,2. Тогда, применяя формулу Бернулли, получаем:
.
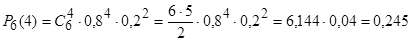4.В партии, содержащей 10 деталей, имеется 6 стандартных. Наудачу отобраны 2 детали. Построить ряд распределения дискретной случайной величины 
– числа стандартных деталей среди двух отобранных. Вычислить 
, 
, 
.
Решение. Ряд распределения для дискретной случайной величины имеет вид:
| xi | x 1 | x 2 | x 3 | … | xn |
| pi | p 1 | р 2 | р 3 | … | рn |
– возможные значения случайной величины ,
–вероятности, с которыми СВ принимает эти значения.
В данной задаче СВ ‑ число стандартных деталей среди двух отобранных. Стандартных деталей может не быть ни одной (т.е. значение СВ 0), одна или две. Таким образом, возможные значения СВ 0, 1, 2. Вычислим вероятности, с которыми СВ принимает эти значения. Воспользуемся классическим определением вероятности. Среди двух выбранных двух деталей 0 стандартных означает, что две детали выбраны из 4 имеющихся нестандартных. Всего таких возможностей 
. Всего способов выбрать две детали из 10 имеющихся 
. Таким образом,
Среди двух выбранных двух деталей 1 стандартная означает, что одна деталь выбрана из 6 имеющихся стандартных и одна деталь выбрана из 4 имеющихся нестандартных. Всего таких возможностей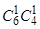 
. Всего способов выбрать две детали из 10 имеющихся . Таким образом,
.
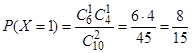Среди двух выбранных двух деталей 2 стандартные означает, что две детали выбраны из 6 имеющихся стандартных. Всего таких возможностей 
. Всего способов выбрать две детали из 10 имеющихся . Таким образом,
.
Сумма вероятностей должна быть равна 1. Действительно, 
.
Получим ряд распределения:
| xi | |||
| pi | 
| 
| 
|
Вычислим числовые характеристики рассматриваемой дискретной случайной величины.
Математическим ожиданием случайной величины называется ее среднее значение, вычисляемое по формулам:
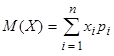– для дискретной случайной величины,
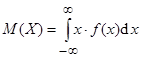– для непрерывной случайной величины.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения:
.
Дисперсия вычисляется по формулам:
– для дискретной случайной величины,
– для непрерывной случайной величины.
Средним квадратическим отклонением (с.к.о.) случайной величины 
называется корень квадратный из дисперсии:
В данной задаче
.
Дисперсия
.
Среднее квадратическое отклонение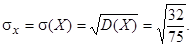 
5. Задана функция распределения
Найти плотность распределения, построить графики функции распределения и плотности, найти 
Решение. Для нахождения плотности распределения воспользуемся формулой 
. Получим
Графики функций 
и 
имеют вид:
Вероятность того, что случайная величина примет значение, заключенное в интервале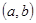 
, находят по формуле:
В данной задаче
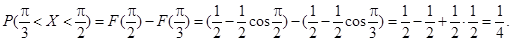
6.Двумерная случайная величина 
распределена по закону
| Х \ Y | ||
| 0,15 | 0,3 | |
| 0,06 | 0,1 | |
| 0,25 | 0,03 | |
| 0,04 | 0,07 |
Найти распределения случайных величин 
и 
, условное распределение случайной величины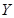 
при условии, что 
. Вычислить ковариацию. Исследовать зависимость СВ и .
Решение. Зная матрицу распределения системы двух СВ, можно легко найди ряды распределения составляющих величин. Нужно сложить вероятности в таблице по строкам и столбцам:
, 
,
, 
.
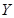Таким образом, СВ и распределены следующим образом:
Случайная величина принимает значения 1, 3, 4, 8 с вероятностями
Распределение СВ имеет вид
|
| ||||
| 0,45 | 0,16 | 0,28 | 0,11 |
Случайная величина 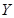принимает значения 3, 6 с вероятностями
Распределение СВ 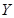имеет вид
|
| ||
|
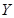
| 0,5 | 0,5 |
Зная закон распределения двумерной дискретной СВ, можно вычислить условные законы распределения составляющих. Для СВ условные вероятности вычисляют по формулам:
.
Аналогично для составляющей :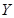
.
Сумма вероятностей условного распределения равна 1.
Найдем условное распределение случайной величины 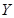при условии, что . Эта СВ принимает значения 3 и 6. Найдем условные вероятности при условии 
Получим условное распределение
|
| ||
| 
| 
|
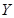
Ковариация – это числовая характеристика системы СВ. Ее вычисляют по формуле
.
Ковариацию можно также представить в виде:
.
Для дискретных СВ формула имеет вид:
Вычислим ковариацию
Исследуем вопрос о зависимости случайных величин. Можно использовать следующие свойства:
1) Ковариация двух независимых СВ равна 0. Следовательно, если она не равна нулю, то случайные величины зависимы. В данной задаче ковариация отлична от нуля, а значит, случайные величины зависимы.
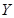2) Если и ‑ независимые СВ, то каждый элемент матрицы равен произведению соответствующих элементов рядов распределения СВ и :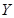 
.Если последнее равенство не выполнено, то случайные величины зависимы. Проверим выполнение этого условия в нашей задаче: 
, следовательно, случайные величины зависимы. Для того, чтобы установить независимость СВ, нужно проверить выполнение свойства для всех пар вероятностей.
3) Если условные и безусловные распределения случайных величин, входящих в систему, совпадают, то случайные величины независимы. В противном случае они зависимы. В данной задаче распределение СВ 
(безусловное распределение) не совпадает с условным распределением СВ при условии, что 
, следовательно, случайные величины зависимы.
7. СВ имеет нормальное распределение с известным с.к.о. 
. Найти доверительный интервал для неизвестного математического ожидания 
по выборочной средней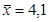 
, если объем выборки 
и задана надежность оценки 
.
Решение. Найдем 
из условия 
или 
. По таблице значений функции Лапласа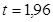 
. Точность оценки 
. Доверительный интервал имеет вид 
. Для 
получаем доверительный интервал 
.
8. На основании данных о среднемесячной заработной плате и числе уволившихся за год работников 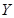на 6 однотипных предприятиях с одинаковым числом работников построить уравнение линейной регрессии 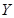на и найти выборочный коэффициент корреляции. Проверить гипотезу о значимости выборочного коэффициента корреляции при уровне значимости 
Среднемесячная зарплата  (млн. руб.)
| 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 |
Число уволившихся работников  (чел.)
|
Решение. Решим задачу двумя способами:
1-й способ: Уравнение линейной регрессии имеет вид:
.
Для нахождения коэффициентов вычислим
, 
,
, 
,
.
Коэффициенты находим по формулам:
,
.
Получим уравнение линейной регрессии 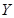на :
.
2-й способ. Воспользуемся уравнением линейной регрессии в виде:
.
По данным выборки вычислим выборочные средние
,
выборочные средние квадратические отклонения
а также выборочный коэффициент корреляции
.
Подставим найденные значения параметров в указанное выше уравнение, получим
.
После несложных преобразований получим уравнение в виде:
.
Ответ: уравнение линейной регрессии 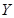на имеет вид: , выборочный коэффициент корреляции 
.
Решим следующую задачу: при заданном уровне значимости 
проверить гипотезу 
(коэффициент корреляции генеральной совокупности равен 0) при альтернативной гипотезе 
. Если нулевая гипотеза отвергается, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля (кратко говоря, значим), а случайные величины и 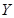коррелированны и связаны линейной зависимостью.
Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции незначим, а случайные величины и 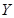не коррелированны.
Вычислим наблюдаемое значение критерия
.
Поскольку альтернативная гипотеза имеет вид , то критическая область двусторонняя.
По 
и числу степеней свободы 
находим по таблице критических точек распределения Стьюдента 
. Поскольку 
, то гипотезу 
отвергаем, т.е. коэффициент корреляции значимо отличается от нуля (другими словами, значим), следовательно, случайные величины и 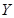коррелированны.
Дата добавления: 2015-09-03; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Суть неокейсианского учения | | | Тейт Черный Кречет |