Третья задача кинематического анализа

Определение недостающих размеров

Определяем длину кривошипа:

Определяем длину шатуна:

Определяем масштабный коэффициент:

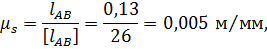
где – длина кривошипа на чертеже.

Определяем размеры шатуна на чертеже:

Определим положение центра масс шатуна:

Построение плана скоростей

Определяем угловую скорость ведущего звена:

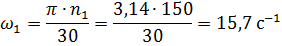
Определяем скорость точки B:

Определяем масштабный коэффициент плана скоростей:

где - длина вектора скорости точки B на чертеже.

Измеряем на чертеже длины векторов скоростей точки С и S₂ результаты измерения заносим в таблицу 1.

Таблица 1

, мм		41,72		28,99		28,99		41,72
, мм	32,5	44,05		40,32	32,5	40,32		44,05
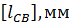
		35,92		35,92		35,92		35,92

Определяем скорости точек:

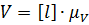
Числовые значения скоростей приведены в таблице 2.

Таблица 2

		1,7	2,04	1,18		1,18	2,04	1,7
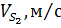
	1,326	1,797		1,645	1,326	1,645		1,797
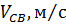
	2,04	1,465		1,465	2,04	1,465		1,465

Определяем угловые ускорения шатуна:

Числовые значения приведены в таблице 3.

Таблица 3

	3,93	2,823		2,823	3,93	2,823		2,823

Структурный анализ механизма

Звенья:

1. Неподвижная направляющая, опора;

2. Кривошип;

3. Шатун;

4. Ползун.

А (1,2) – низшая, вращательная кинематическая пара 5 класса,
В (2,3) – низшая, вращательная кинематическая пара 5 класса,
С (3,4) – низшая, вращательная кинематическая пара 5 класса,
D (4,1) – низшая, поступательная кинематическая пара 5 класса.

Определяем степень подвижности:

Лишних степеней свободы, высших кинематических пар, пассивных связей в механизме нет.

Третья задача кинематического анализа

Определяем ускорения звена AB:

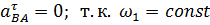
Определяем масштабный коэффициент плана ускорений:

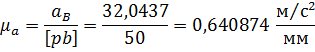
где - длина вектора скорости a_B на чертеже.

Определяем ускорения группы Ассура в каждом положении:

Определяем нормальную составляющую ускорения a_CB:

Числовые значения приведены в таблице 4.

Таблица 4

, м/с^2	8,0159	4,136		4,136	8,0159	4,136		4,136
	12,508	6,454		6,454	12,508	6,454		6,454

Определяем длину нормальной составляющей ускорения a_CB на чертеже:

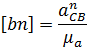
Числовые значения приведены в таблице 3.

Измеряем отрезки плана ускорений, записываем в таблицу 5.

Таблица 5

	62,51	35,55	12,94	35,16	62,51	35,16	12,94	35,55
	54,3785	42,22	32,81	42,11	54,3785	42,11	32,81	42,22
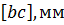
	12,51	35,36	51,65	35,36	12,51	35,36	51,65	35,36
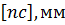
		34,76	51,65	34,76		34,76	51,65	34,76

Умножаем числа из таблицы 4 на масштабный коэффициент плана ускорений. Получим действительные значения ускорений всех точек механизма (таблица 6).

Таблица 6

	40,061	22,783	8,2929	22,533	40,061	22,533	8,2929	22,783
	34,8498	27,0577	21,027	26,987	34,8498	26,987	21,027	27,0577
	8,017	22,661	33,1	22,661	8,017	22,661	33,1	22,661
		22,2768	33,1	22,277		22,277	33,1	22,2768

Находим значения угловых ускорений звеньев механизма:

Числовые значения приведены в таблице 7.

Таблица 7

		11,5616	17,179	11,5618		43,43	17,179	11,562

Дата добавления: 2015-10-23