Спин фотона. Правила отбора

Рассмотрим поляризованный по кругу свет исходя из классических представлений. Он представляет собой наложение двух поляризованных во взаимно перпендикулярных направлениях когерентных колебаний, сдвинутых друг относительно друга на фазу . В этом случае суммарный

вектор напряженности электрического поля поворачивается по кругу с угловой скоростью, равной частоте света (Рис. 8.3, а).

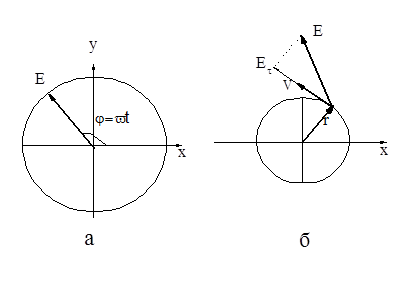
Рис. 8.3

Если такой свет падает на атом, электроны в нем начнут колебаться в двух взаимно перпендикулярных направлениях с одинаковой амплитудой и частотой и со сдвигом фаз, равным 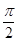. В результате электрон начнет двигаться по окружности (Рис. 8.3, б). Вычислим работу, которая совершается силами поля над электроном

. (8.7)

Отсюда можно получить скорость подачи энергии электрону

, (8.8)

где – скорость движения электрона.

Из Рис. (8.3, б) видно, что электрон приобретает, кроме того, и момент количества движения, так как на него действует вращательный момент внешних сил, равный . Тогда по второму закону Ньютона, скорость изменения момента количества движения электрона, должна быть равна моменту внешних сил

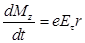. (8.9)

Поделим равенство (8.8) на (8.9), в результате получим

. (8.10)

Проинтегрировав равенство (8.10), получаем соотношение между энергией и моментом количества движения электрона

, (8.11)

которое должно быть справедливо и для циркулярно поляризованного света.

Применим соотношение (8.11) к фотону.

, (8.12)

откуда видно, что . Вспоминая соотношение между проекцией момента импульса на ось и спиновым квантовым числом , находим, что спин фотона равен . Фотоны – это бозоны.

Плоско поляризованный свет может быть представлен в виде суперпозиции световых волн с правой и левой циркулярной поляризацией. Действительно, результатом сложения двух равных по модулю векторов, вращающихся в противоположные стороны с одинаковой угловой скоростью, будет вектор всегда направленный вдоль одной прямой, что и есть плоско поляризованный свет. С точки зрения квантовой механики, это означает, что плоско поляризованный свет представляет собой совокупность фотонов, имеющих проекцию момента импульса на ось , равную 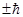. Суперпозиция таких состояний фотонов приводит к состоянию с неопределенным моментом количества движения, то есть плоско поляризованный свет не обладает определенным моментом импульса. Однако при измерении мы будем получать с равной вероятностью либо право винтовой фотон, имеющий проекцию момента импульса на ось , равную , либо лево винтовой фотон с проекцией момента импульса, равной .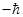

Теперь легко понять упоминавшиеся выше правила отбора для переходов электронов в атоме под действием света. Возможны только такие переходы, для которых выполнено соотношение: . Очевидно, что эти правила отбора есть следствие закона сохранения момента импульса. Пусть в исходном состоянии электрон находился в состоянии с орбитальным квантовым числом, равным . Падающий фотон может находиться в одном из двух состояний со спиновым квантовым числом, равным . При поглощении фотона его момент количества движения передается атому. Отсюда получаем, что при переходе электрона его орбитальное квантовое число должно обязательно измениться следующим образом:

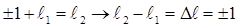. (8.13)

Аналогичные соотношения будут выполняться и при испускании фотона

(8.14)

Это означает, что в спектрах поглощения/испускания будут наблюдаться переходы

, , (8.15)

Лекция 9

Дата добавления: 2015-10-23