Принцип Паули. Многоэлектронные атомы.

Лекция 7

Атом водорода.

Атом водорода представляет собой систему, состоящую из положительно заряженного неподвижного ядра и движущегося вокруг него электрона. Уравнение Шредингера для атома водорода имеет вид:

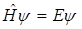, где 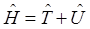, (7.1)

где 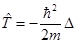– оператор кинетической энергии электрона,

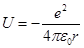– потенциальная энергия электрона в поле ядра.

Поле, в котором движется электрон, является сферически симметричным, поэтому от декартовых координат в операторе Лапласа нужно перейти к сферическим координатам.

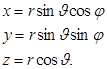(7.2)

В сферических координатах оператор Лапласа распадается на два слагаемых, в первое слагаемое входят производные только по 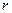, во второе – производные только по угловым переменным 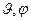: . В классической механике полная кинетическая энергия представляет собой сумму кинетических энергий поступательного и вращательного движений

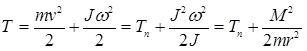, (7.3)

где 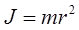– момент инерции материальной точки,

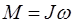– момент импульса частицы.

В квантовой механике, согласно принципу соответствия, равенство (7.3) нужно заменить на операторное

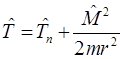. (7.4)

Соответствующий расчет показывает, что угловая часть оператора Лапласа представляет собой квадрат оператора момента импульса .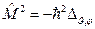

Тогда уравнение Шредингера принимает вид

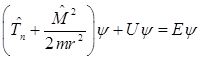, (7.5)

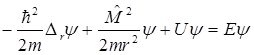. (7.6)

Поскольку потенциальная энергия не зависит от угловых переменных, решение будем искать в виде

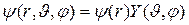, (7.7)

где 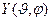– собственная функция оператора квадрата момента импульса.

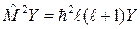. (7.8)

Подставим функцию (7.7) в уравнение Шредингера. Оператор момента импульса действует только на функцию, зависящую от угловых переменных, поэтому получаем

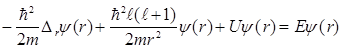. (7.9)

Подставив в (7.9) выражение для потенциальной энергии, получаем уравнение для радиальной волновой функции

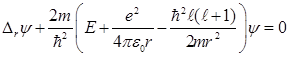. (7.10)

К этому уравнению нужно добавить граничные условия. Поскольку электрон связан с ядром, то вероятность обнаружить его на больших расстояниях от ядра должна быстро убывать с увеличением расстояния. Это требование накладывает условия на асимптотическое поведение волновой функции

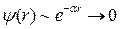при 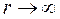. (7.11)

Оказывается, что это условие может быть выполнено только для отрицательных значений энергии, равных

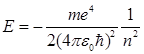, (7.12)

где 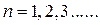– называется главным квантовым числом и представляет собой номер уровня.

Это те же уровни энергии в атоме водорода, что были получены в теории Бора. Для всех остальных значений параметра 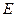в уравнении Шредингера волновая функция неограниченно возрастает при отдалении электрона от ядра, что лишено физического смысла. Таким образом, мы естественным образом проквантовали энергию электрона в атоме водорода.

В атоме водорода энергия электрона зависит только от главного квантового числа 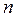. Во всех остальных атомах, энергия определяется главным 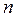и орбитальным 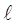квантовыми числами. Из уравнения (7.10) видно, что радиальная волновая функция зависит от главного и орбитального квантовых чисел, а угловая волновая функция зависит от орбитального и магнитного квантовых чисел. Таким образом, собственные функции оператора Гамильтона могут быть представлены в виде:

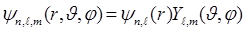. (7.13)

Радиальная волновая функция будет ограничена во всем пространстве только при выполнении условия .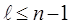

Состояния с заданным моментом количества движения обозначаются малыми буквами латинского алфавита:

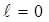1 2 3 4 5

.

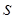
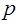
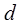
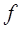
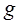
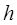Для основного состояния 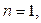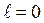. Это состояние обозначается символом . В первом возбужденном состоянии главное квантовое число 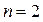, орбитальное квантовое число может принимать два значения 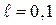. Это состояния обозначаются символами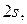 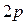. Во втором возбужденном состоянии 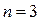, , 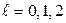соответственно получаем состояния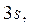 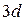. Всем состояниям с ненулевым орбитальным квантовым числом соответствует 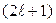состояние с различными значениями магнитного квантового числа .

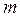Как уже упоминалось выше, энергия в атоме водорода не зависит от орбитального квантового числа. Состояния с одинаковой энергией называются вырожденными, а число различных состояний с данным значением энергии называется кратностью вырождения. Вычислим кратность вырождения уровней в атоме водорода. Число возможных состояний с заданным 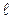равно 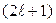, а для данного 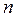, 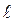принимает значения от 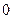до 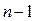. Следовательно, число различных состояний, соответствующих данному 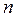, равно

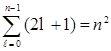. (7.14)

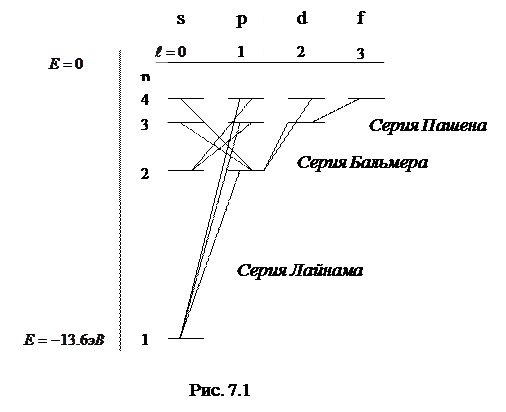
Схема уровней атома водорода представлена на рис. 7.1.

Рассмотрим спектр атома водорода. Ниже будет показано, что возможны только переходы, для которых выполняется правило отбора 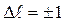, то есть орбитальное квантовое число может измениться в результате перехода только на единицу. Тогда серия Лаймана в спектре испускания образуется в результате переходов электрона

, ,

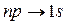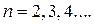серия Бальмера соответствует переходам

, , (.)

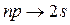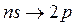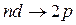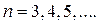Спектрам поглощения соответствуют обратные переходы: 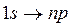для серии Лаймана, 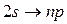, , 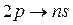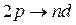для серии Бальмера и т. д.

Обратимся вновь к уравнению Шредингера для радиальной волновой функции. Из выражения (7.10) видно, что оно сводится к уравнению одномерного движения с эффективным потенциалом

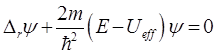, (7.14)

где 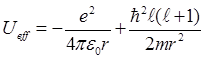. (7.15)

Первое слагаемое в (7.15) представляет собой потенциальную энергию кулоновского притяжения электрона к ядру, второе – центробежное отталкивание. Вид эффективного потенциала в зависимости от расстояния электрона от ядра представлен на рис. 7.2.

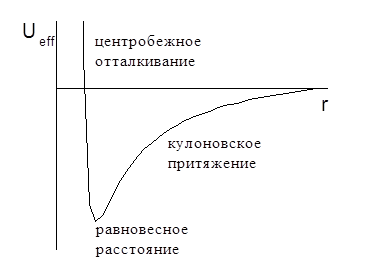
Рис. 7.2

На больших расстояниях от ядра преобладает кулоновское притяжение, но на малых расстояниях основной вклад в энергию дает центробежное отталкивание. На некотором расстоянии эти взаимодействия уравновешивают друг друга. Для того чтобы найти равновесное расстояние,

возьмем производную от эффективной потенциальной энергии и приравняем полученное выражение нулю.

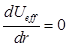
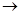
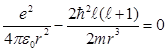. (7.16)

Отсюда находим выражение для равновесного расстояния

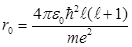. (7.17)

Как и следовало ожидать, равновесное расстояние электрона от ядра возрастает с увеличением момента количества движения. Центробежная сила как бы отбрасывает электрон от кулоновского центра.

Состояние электрона в атоме водорода описывается волновой функцией (7.13). Зная волновую функцию, можно найти вероятность обнаружить электрон в бесконечно малом объеме с координатами :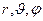

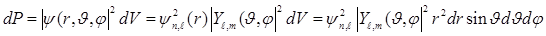. (7.18)

Если проинтегрировать это выражение по всем значениям углов 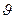и 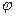, то мы получим вероятность обнаружить электрон в шаровом слое радиуса 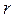и толщиной .

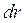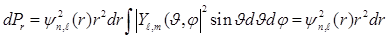, (7.19)

так как угловые волновые функции нормированы на единицу.

Из равенства (7.19) получаем плотность вероятности обнаружить электрон на расстоянии 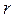от ядра

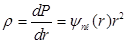. (7.20)

На рис. 7.3 приведены графики плотности вероятности 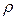для состояни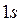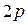й , и . За единицу масштаба для оси 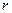выбран Боровский радиус .

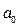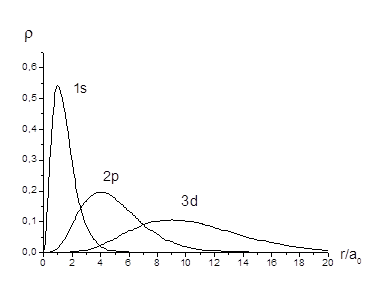
Рис. 7.3

Из графика видно, что для этих состояний плотность вероятности обнаружить электрон достигает максимума на расстояниях, равных Боровским радиусам. Однако есть отличная от нуля вероятность обнаружить электрон и на других расстояниях от ядра. В соответствии с этим электроны рассматриваются как размазанные в пространстве и образующие вокруг ядра электронное облако.

Проинтегрируем теперь выражение (7.18) по всем расстояниям 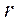от 0 до 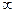. В этом случае мы найдем вероятность обнаружить электрон в телесном угле :

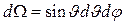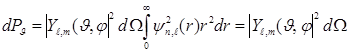. (7.21)

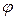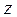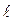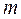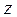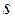Расчет показывает, что эта вероятность не зависит от угла . Это означает, что в плоскости, перпендикулярной оси , распределение вероятности нахождения электрона симметрично. Распределение вероятности (7.21) определяется двумя квантовыми числами и , то есть зависит от величины полного момента и его проекции на ось . Для состояния распределение вероятности не зависит и от угла 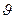, то есть оказывается сферически симметричным. Очевидно, что если орбитальный момент импульса равен нулю, то повороты в пространстве ничего не меняют в системе, поэтому распределение вероятности для этого состояния должно быть сферически симметричным (Рис. 7.4, а). Для состояний с отличным от нуля орбитальным моментом распределение вероятностей зависит от азимутального угла 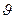. Эта зависимость для 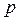состояний представлена на рис. 7.4, б.

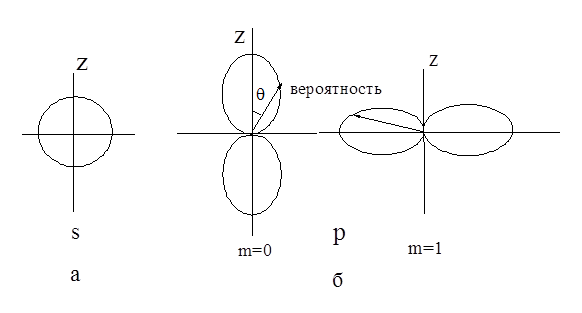
Рис. 7.4

Плотность вероятности обнаружить электрон в точке с координатами 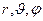дается выражением:

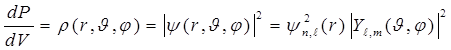. (7.22)

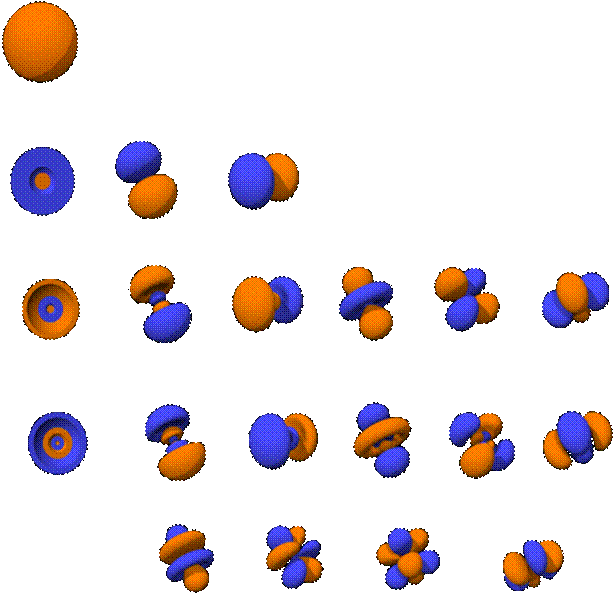
Эта плотность вероятности описывает распределение электронной плотности в атоме, которое зависит от квантового состояния электрона (Рис.7.5). В 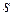– состоянии электронная плотность максимальна в центре и не зависит от направления (сферически симметрична). В 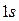– состоянии она монотонно спадает при увеличении расстояния электрона от ядра. В возбужденных 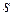– состояниях плотность вероятности обращается в нуль на некотором расстоянии от ядра, а затем снова принимает ненулевое значение. Для состояний с 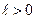электронная плотность равна нулю в центре и зависит от направления. Обращение электронной плотности в нуль в центре при 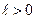естественный результат, ведь электрону трудно иметь большой момент, когда плечо момента очень мало. По этой причине, чем больше орбитальное квантовое число, тем дальше амплитуды отталкиваются от центра.

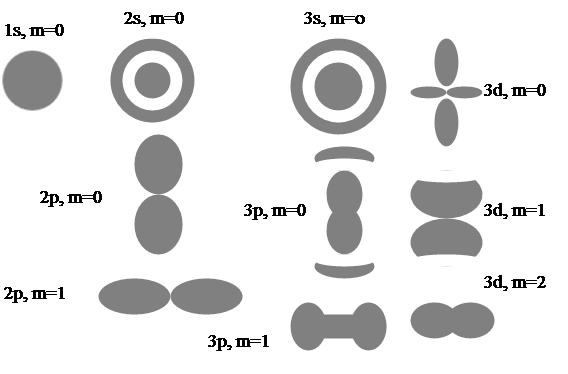
Рис. 7.5

Рис. 7.5 наглядно иллюстрирует кардинальное отличие квантовых представлений о строении атома от классических. Согласно квантовой механике электроны размазаны по объему атома, образуя электронные облака сложной конфигурации. Ни о каком движении электронов по определенным орбитам говорить совершенно неправомерно.

Лекция 8

Спин электрона. Принцип Паули. Многоэлектронные атомы.

8.1. Спин электрона.

Рассмотрим спектры атомов щелочных металлов. В этих атомах имеется один валентный электрон, находящийся в 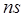состоянии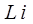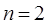, для , для 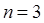и т.д. Мы уже говорили о том, что во всех атомах, кроме водорода, энергия зависит от главного и орбитального квантовых чисел, то есть в щелочных атомах снимается вырождение по орбитальному квантовому числу. 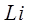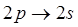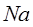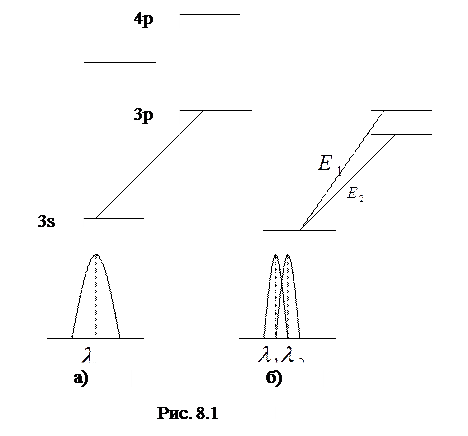Следовательно, можно было бы ожидать, что в спектрах атома будут наблюдаться линии, соответствующие переходу , в спектре атома – линии, соответствующие переходу 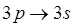. На рис. 8.1 (а) приведено ожидаемое расположение энергетических уровней в атоме натрия и показана спектральная линия, соответствующая 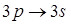переходу валентного электрона. Однако исследование спектров при помощи приборов с большой разрешающей способностью показало, что каждая линия, соответствующая 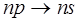переходу в щелочных атомах является двойной, то есть состоит из двух близко расположенных линий. А это означает, что в этих атомах имеется два близко расположенных уровня энергии (Рис. 8.1, б). Это было неожиданно, так как не было лишних квантовых чисел, которыми можно было бы эти уровни описать.

Для объяснения расщепления уровней энергии в щелочных металлах

Гаудсмит и Уленбек выдвинули гипотезу о том, что электрон обладает собственным моментом импульса, не связанным с его движением в пространстве. Этот собственный момент был назван спином. Поначалу думали, что спин можно представить себе, как вращение электрона вокруг своей оси. Однако более тщательное исследование показало, что это не так. Сейчас считается, что спин это внутренне свойство электрона, присущее ему, также как заряд или масса.

Спин оказался присущ не только электронам, но и другим элементарным частицам. Спиновое квантовое число частицы 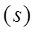может быть целым или полуцелым. По значению спина все частицы делятся на два класса. Частицы с целым спином называются бозонами, частицы с полуцелым спином называются фермионами. Как мы увидим ниже, фермионы и бозоны имеют совершенно различное коллективное поведение.

Электрон – это фермион, его спиновое квантовое число 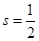. Зная спиновое квантовое число можно вычислить собственный момент импульса электрона по обычной схеме:

. (8.1)

Проекция спина на заданное направление может принимать два значения

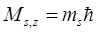
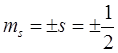. (8.2)

Рассмотрим теперь, как существование спина может объяснить дуплетную структуру линий в спектре щелочных металлов. Электрон обладает двумя моментами импульса – орбитальным 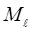и спиновым 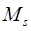. Из этих двух моментов складывается полный момент импульса электрона в атоме. Величина полного момента определяется квантовым числом , которое может принимать значения:

, (8.3)

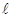где и 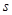– соответственно азимутальное и спиновое квантовые числа.

Зная квантовое число полного момента можно рассчитать полный момент импульса электрона и его проекцию на ось по обычной схеме:

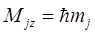, . (8.4)

При 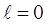квантовое число полного момента принимает только одно значение 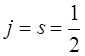. При 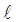, отличном от нуля, возможны два значения квантового числа полного момента 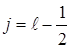и ,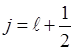

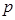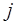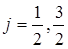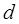которые соответствуют двум возможным взаимным ориентациям орбитального и спинового моментов, параллельном и антипараллельном. В частности, для состояния принимает два значения: , для состояния 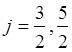. Таким образом, состояние электрона в атоме характеризуется квантовыми числами орбитального, спинового и полного моментов и его принято обозначать следующим символом

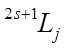, (8.5)

где 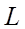– орбитальное квантовое число, 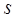– спиновое квантовое число,

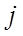– квантовое число полного момента.

Число 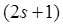называется мультиплетностью состояния. В рассматриваемом случае мультиплетность равна двум, то есть каждое состояние с ненулевым орбитальным моментом расщепляется на два состояния, образующих дуплет. В этих обозначениях состояния валентного электрона в атоме натрия, например, можно представить следующим образом

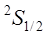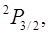
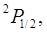
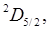
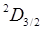, . (8.6)

Поскольку электроны обладают зарядом, то с механическими моментами связаны магнитные моменты электрона, которые взаимодействуют друг с другом. Энергия этого взаимодействия, называемого спин-орбитальным взаимодействием, зависит от взаимной ориентации орбитального и спинового моментов. Следовательно, состояния с различными 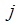будут обладать разной энергией. Таким образом, вместо одного уровня, соответствующего 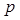состоянию, в атомах щелочных металлов появляется два уровня с разными значениями 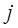. Соответственно в спектрах этих металлов появляется две близко расположенные линии. Схема уровней энергии в атоме натрия представлена на рис. 8.2.

Принцип Паули. Многоэлектронные атомы.

Как мы уже говорили, по значению спина все элементарные частицы делятся на два класса – фермионы и бозоны. Фермионы обладают полуцелым спином – это электроны, протоны, нейтроны. Фермионы это частицы, которые входят в состав вещества. Бозоны имеют целый спин и, как мы увидим ниже, являются переносчиками взаимодействия между фермионами. Различная роль этих частиц в устройстве мира связана с их различным коллективным поведением.

Для фермионов справедлив принцип Паули, согласно котором

у вероятность обнаружить два фермиона в одной системе в одном и том же состоянии равна нулю. Этому свойству фермионов мы обязаны всему многообразию мира, который нас окружает.

Бозоны ведут себя совершенно иначе. Если в данном состоянии уже находится 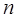бозонов, то вероятность того, что новый бозон окажется в том же состоянии, растет пропорционально 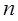. То есть бозоны стремятся все оказаться в одном и том же состоянии. Этим свойством бозонов, например, объясняются такие явления как сверхпроводимость и сверхтекучесть.

Но вернемся к принципу Паули. Он объясняет, почему электроны не конденсируются в одном состоянии с наименьшей энергией, а заполняют, по мере увеличения их числа, все более высокие уровни энергии. Таким образом, возникает все многообразие атомов с различными свойствами. Волновая функция, описывающая состояние электронов в атоме, зависит от четырех квантовых чисел 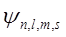. Здесь 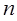– главное квантовое число или номер уровня, 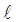– орбитальное квантовое число, 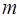– магнитное квантовое число и 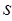– спиновое квантовое число.

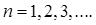
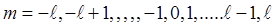
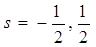
Всего при данном 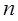получается 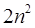различных состояний.

Принцип Паули говорит о том, что в атоме не может быть двух электронов, обладающих одинаковой совокупностью квантовых чисел. Поэтому на первом уровне может находиться не более двух электронов, на втором – не более 8 электронов, на третьем – не более 18 и так далее. Принцип Паули дает объяснение периодической повторяемости свойств атомов, открытой Менделеевым. Проследим построение периодической системы элементов.

Водород имеет один электрон в 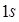состоянии, электронная конфигурация водорода может быть записана следующим образом – .

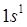Гелий 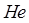имеет два электрона в 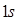состоянии с противоположно направленными спинами. Электронная конфигурация гелия будет 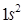. На первом уровне не может находиться больше двух электронов, поэтому третий электрон в атоме 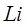начинает заполнение второго энергетического уровня. Электронная конфигурация

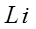(литий) – ,

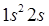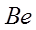(бериллий) – ,

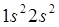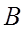(бор) – .

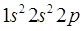Далее идет заполнение шести 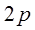состояний, которое заканчивается на неоне:

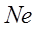(неон) – .

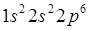Неон имеет полностью заполненный второй уровень. С натрия начинается заполнение третьего уровня энергии.

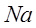(натрий) – ,

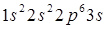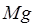(магний) – .

Заполнение 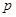состояний третьего уровня начинается на алюминии

,

и заканчивается на аргоне, его электронная конфигурация имеет вид

– .

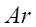Далее должно было бы начинаться заполнение 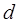состояний третьего уровня. Но состояния с большим орбитальным моментом обладают большой центробежной энергией. Энергия связи 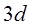электронов с ядром оказывается меньше, чем у электронов. Поэтому сначала заполняются два 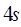состояния в калии и кальции, имеющие конфигурации:

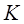(калий) – ,

(кальций) – .

И только после этого начинается заполнение 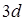состояний у скандия

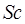(скандий) – .

Заполнение 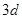оболочки заканчивается у меди

.

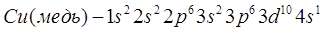Большинство свойств атомов определяется строением их внешних электронных оболочек, в которых электроны связаны сравнительно слабо. Периодичность в свойствах элементов определяется сходством внешних электронных оболочек атома. Например, атомы лития, натрия, калия имеют по одному электрону на внешней оболочке и сходны по многим своим физическим и химическим свойствам. Атомы, имеющие полностью заполненные оболочки (инертные газы), наиболее стабильны, они не вступают ни в какие химические реакции. Электроны во внешних незаполненных оболочках легко подвергаются внешним воздействиям. При сближении атомов возникают сильные взаимодействия, которые могут приводить к образованию молекул. В химической связи участвуют электроны внешних оболочек. Механизм отдачи или присоединения валентных электронов лежит в основе большинства химических реакций. Энергетически оказываются выгодными отдача электронов атомами с менее чем на половину заполненной 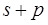подгруппой и присоединение электронов атомами с более чем наполовину занятой 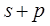подгруппой.

Внешними электронами определяются и магнитные свойства атомов. В атомах с полностью заполненной оболочкой механический и магнитный момент атома равен нулю и, следовательно, такие атомы будут диамагнитными. Магнитные момента атомов с частично заполненными оболочками, как правило, не равны нулю, такие атомы являются парамагнитными. Ферромагнитными будут атомы с недостроенными электронными оболочкам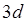и или 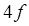, обладающие не равным нулю значением результирующего спинового магнитного момента (железо, кобальт, никель). Большая собственная намагниченность ферромагнетиков объясняется сильным спин-спиновым взаимодействием магнитных моментов. В результате этого взаимодействия энергетически выгодным оказывается упорядоченное состояние с параллельной ориентацией спиновых моментов соседних атомов. Это приводит к образованию доменов, областей, обладающих спонтанной намагниченностью.

Дата добавления: 2015-10-23