Собственные векторы и собственные значения линейного оператора

Определение. Вектор называется собственным вектором линейного оператора , если существует такое число , что . Число называется соответствующим вектору собственным значением оператора .

Замечание. Поскольку каждый линейный оператор в некотором базисе однозначно задается квадратной матрицей A, то определение собственного вектора (представленного в виде вектор-столбца) можно записать так: .

Вопрос. Как найти собственные значения и собственные векторы?

Предположим, что – собственный вектор, а – соответствующее ему собственное значение линейного оператора , задаваемого в некотором базисе , , …, матрицей A. Тогда, как указывалось, , или в компонентах:

Û

Получили однородную систему n линейных уравнений с n неизвестными. Для существования ненулевого решения которой необходимо и достаточно, чтобы детерминант этой системы был равен нулю, т.е.

.

Левая часть последнего равенства совпадает при со значением определителя матрицы . Этот определитель является многочленом степени n относительно . Он называется характеристическим многочленом линейного оператора (Часто говорят: характеристическим многочленом матрицы A.) Итак, показано, что каждое собственное значение линейного оператора является корнем его характеристического многочлена.

Верно и обратное. Каждый корень характеристического многочлена линейного оператора будет являться его собственным значением.

Действительно, соответствующие собственные векторы находятся из системы уравнений

которая в этом случае обязательно имеет ненулевые решения, т.к. ее детерминант равен нулю.

Теорема 1. Характеристический многочлен линейного оператора не зависит от выбора базиса.

Доказательство. Пусть – характеристический многочлен оператора (матрицы A) в базисе , ,..., . Предположим, что «новый» базис , ,..., получается из «старого» , ,..., с помощью матрицы перехода C. Тогда характеристический многочлен оператора в базисе , ,..., равен

■

Сделаем несколько важных замечаний относительно собственных значений и собственных векторов линейного оператора.

1. Если оператор задается единичной матрицей E, то все ненулевые векторы L являются собственными (с ).

2. Если оператор задается нулевой матрицей, то все ненулевые векторы L являются собственными (с ).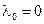

3. Если – собственный вектор оператора (с собственным значением ), то вектор также является собственным (с тем же собственным значением ).

Действительно, ■

Сформулируем теперь три утверждения, которые примем без доказательства.

Утверждение 1. Собственные векторы линейного оператора, соответствующие попарно различным собственным значениям, линейно независимы.

Утверждение 2. Собственные векторы линейного оператора, задаваемого в некотором базисе симметрической матрицей, соответствующие попарно различным собственным значениям, взаимно ортогональны.

Утверждение 3. Собственные значения линейного оператора, задаваемого в некотором базисе симметрической матрицей, являются действительными числами.

Пример. Найти собственные значения и собственные векторы линейного оператора, задаваемого в некотором базисе матрицей

.

Решение. Найдем корни характеристического многочлена :

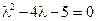Û Û

Найдем теперь собственные векторы, отвечающие собственным значениям и .

1) Рассмотрим . Тогда для нахождения собственных векторов , надо решить однородную систему линейных уравнений

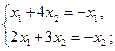Û Û Û

Û Û Û .

Итак, семейство собственных векторов, соответствующих собственному значению имеет вид , где , 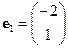– один из собственных векторов этого семейства.

2) Рассмотрим . Тогда для нахождения собственных векторов , надо решить однородную систему линейных уравнений

Û Û Û

Û Û Û .

Итак, семейство собственных векторов, соответствующих собственному значению имеет вид , где , – один из собственных векторов этого семейства.

Теорема 2. Линейный оператор задается в базисе , ,..., диагональной матрицей тогда и только тогда, когда все векторы базиса , ,..., – собственные.

Доказательство. Необходимость. Пусть матрица A оператора в базисе , ,..., имеет диагональный вид

.

Тогда

,

,

……………………………………….

.

Следовательно, все векторы , ,..., – собственные с собственными значениями , , …, соответственно.

Достаточность. Пусть , ,..., – собственные векторы линейного оператора , образующие базис и отвечающие собственным значениям , , …, соответственно, т.е.

,

,

……………………………………….

.

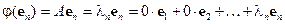Следовательно, по определению матрицы линейного оператора, имеем

.

Таким образом, матрица A – диагональная, а на ее диагонали стоят собственные значения , , …, соответственно ■

Пример (продолжение). Зная собственные значения и собственные векторы линейного оператора, задаваемого в некотором базисе матрицей (см. предыдущий пример)

,

составить матрицу этого линейного оператора в базисе из найденных собственных векторов.

Решение. Согласно рассмотренному выше примеру: и – собственные значения, а 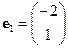, – соответствующие им собственные векторы. Тогда в базисе из собственных векторов , , согласно теореме 2, матрица B линейного оператора имеет диагональный вид

.

Замечание. Матрицу B можно получить и непосредственно из соотношения

,

где C – матрица перехода от «старого» базиса (в котором матрица линейного оператора равна A) к «новому» базису из собственных векторов , . Матрица C имеет следующий вид (Напоминаем, что координаты векторов , в «старом» базисе формируют столбцы матрицы перехода!):

.

Дата добавления: 2015-10-30