
Читайте также:
|
Линейные операторы
Говорят, что в векторном пространстве L задан оператор (или преобразование)  , если каждому вектору
, если каждому вектору  поставлен в соответствие определенный вектор
поставлен в соответствие определенный вектор  .
.
Определение. Оператор (преобразование)  называется линейным, если
называется линейным, если 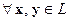 и произвольного числа
и произвольного числа 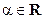 :
:
1) 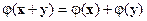 ;
;
2)  .
.
Вектор  называется образом вектора
называется образом вектора  , а вектор
, а вектор  – прообразом вектора
– прообразом вектора  при преобразовании
при преобразовании  .
.
Выберем в L базис  ,
,  ,...,
,...,  . Тогда, если
. Тогда, если
 ,
,
то в силу линейности оператора  имеем:
имеем:
 .
.
Но 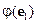 ,
,  ,...,
,...,  также векторы из L, поэтому
также векторы из L, поэтому

Тогда
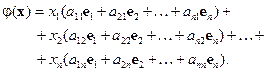
Группируя по «столбцам», получим:
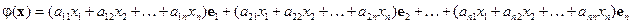 .
.
Если  ,
, 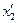 , …,
, …,  – координаты вектора
– координаты вектора  в том же базисе
в том же базисе  ,
,  ,...,
,...,  , т.е. если
, т.е. если
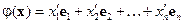 ,
,
то, ввиду единственности разложения вектора по базису, имеем:

Таким образом, каждому линейному оператору  в данном базисе
в данном базисе  ,
,  ,...,
,...,  отвечает матрица
отвечает матрица
 ,
,
столбцы которой образованы коэффициентами разложения векторов 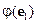 ,
,  ,...,
,...,  по базису
по базису  ,
,  ,...,
,...,  .
.
При этом коэффициенты разложений координат  ,
, 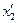 , …,
, …,  вектора
вектора  по координатам вектора
по координатам вектора  образуют строки матрицы A.
образуют строки матрицы A.
Верно и обратное: если в n -мерном векторном пространстве L задан базис, то каждая квадратная матрица A n -го порядка может рассматриваться как матрица некоторого линейного оператора.
Действительно, пусть  ,
,  ,...,
,...,  – базис L и пусть дана матрица A n -го порядка. Обозначим через
– базис L и пусть дана матрица A n -го порядка. Обозначим через  оператор, переводящий произвольный вектор
оператор, переводящий произвольный вектор  в вектор
в вектор 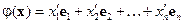 , где
, где

Покажем, что оператор  – линейный. В самом деле, произвольный вектор
– линейный. В самом деле, произвольный вектор  он переводит в вектор
он переводит в вектор  , где
, где
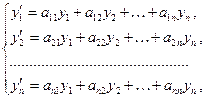
вектор  – в вектор
– в вектор 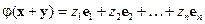 , где
, где
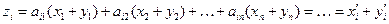 ,
,  .
.
Поэтому 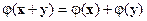 .
.
Далее,  имеем
имеем 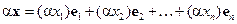 и
и  , где
, где
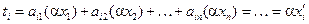 ,
,  .
.
Следовательно,  . А значит, оператор
. А значит, оператор  – линейный.
– линейный.
Итак, если в векторном пространстве L задан базис, то каждому линейному оператору отвечает определенная квадратная матрица n -го порядка и, обратно, каждой подобной матрице отвечает определенный линейный оператор.
Матрица A называется матрицей линейного оператора  .
.
Замечание. Очевидно, что  . При этом, если
. При этом, если 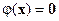 только при
только при 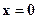 , то оператор
, то оператор  называется невырожденным, если же найдется такой вектор
называется невырожденным, если же найдется такой вектор 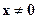 , что
, что 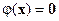 , то оператор
, то оператор  – вырожденный.
– вырожденный.
Пусть A – матрица линейного оператора  . Рассмотрим однородную систему линейных уравнений
. Рассмотрим однородную систему линейных уравнений

Для существования ненулевого решения этой системы (а значит, для существования ненулевого вектора  такого, что
такого, что 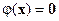 ) необходимо и достаточно, чтобы
) необходимо и достаточно, чтобы 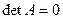 .
.
Итак, оператор  – невырожденный Û
– невырожденный Û 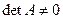 , где A – матрица этого оператора в любом базисе.
, где A – матрица этого оператора в любом базисе.
Пример 1. В четырехмерном векторном пространстве дано линейное преобразование  . Записать это преобразование в координатной форме, если
. Записать это преобразование в координатной форме, если 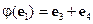 ,
, 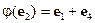 ,
, 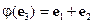 ,
, 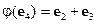 .
.
Решение. Матрица A линейного оператора  имеет следующий вид (Записывается по столбцам!):
имеет следующий вид (Записывается по столбцам!):
 .
.
Поэтому  ,
,  ,
,  ,
,  .
.
Пример 2. В трехмерном векторном пространстве дано линейное преобразование  , которое в координатной форме имеет следующий вид:
, которое в координатной форме имеет следующий вид:
 ,
, 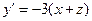 ,
, 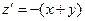 .
.
Является ли данное линейное преобразование вырожденным?
Решение. Матрица A линейного оператора  имеет следующий вид (Записывается по строкам!):
имеет следующий вид (Записывается по строкам!):
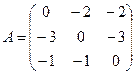 .
.
Поскольку  , то данное линейное преобразование является невырожденным.
, то данное линейное преобразование является невырожденным.
Пример 3. Линейное преобразование  совокупности всех векторов на плоскости Oxy (в правом ортонормированном базисе
совокупности всех векторов на плоскости Oxy (в правом ортонормированном базисе  ,
,  ) заключается в повороте каждого вектора против часовой стрелки на угол
) заключается в повороте каждого вектора против часовой стрелки на угол 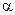 . Найти матрицу этого линейного преобразования и записать
. Найти матрицу этого линейного преобразования и записать  в координатной форме.
в координатной форме.
Решение. Напишем формулы преобразования векторов базиса  ,
,  , опираясь на определение синуса и косинуса:
, опираясь на определение синуса и косинуса:
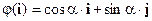 ,
,
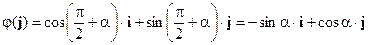 .
.
Тогда матрица A линейного оператора  имеет следующий вид (Записывается по столбцам!):
имеет следующий вид (Записывается по столбцам!):
 .
.
Отметим, что полученную матрицу A называют матрицей поворота.
Тогда в координатной форме преобразование  имеет следующий вид:
имеет следующий вид:
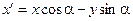 ,
,
 .
.
Дата добавления: 2015-10-30; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример сопроводительного письма | | | Собственные векторы и собственные значения линейного оператора |