Cost, revenue and profit

Vocabulary

1. differential	дифференциальный
2. derivative	производная
3. a slop of the tangent	угловой коэффициент касательной
4. average velocity	средняя скорость
5. motion	движение
6. uniform motion	равномерное движение
7. perform	производить
8. productivity	продуктивность
9. cost	затраты, стоимость
10. revenue	доход
11. profit	прибыль
12. differentiable	дифференцируемый
13. differentiation	дифференцирование
14. mutual	взаимный

Section IV. Differential calculus of the function of one variable.

Derivative of a function and it meaning.

Let function be defined on some set . Give to an argument arbitrary increment , and then function will get an increment 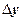. Compose a ratio

.

Definition 1.1: The limit of the ratio of an increment of the function to the corresponding an increment of the argument, when last tends to zero, (provided that this limit exists) is called the derivative of the function at the point .

It is denoted

.

Geometrical meaning of a derivative: the derivative equals to the slope of tangent which is drew to graph of the function at the point with abscissa .

Physical meaning of a derivative: let be the average velocity of the uniform motion of the material point corresponding to time interval from to . Then is a velocity of a point at the moment .

Economical meaning of a derivative: let be the average amount of a work performed by the worker in time interval from to . Then is a productivity of the worker at a point .

Derivative in economic.

Cost, revenue and profit

Suppose that

is the cost of producing the items,

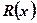is the revenue from selling items,

is the profit from selling items.

Economists often call the derivatives of these functions the marginal values of the functions.

For example, suppose it costs to company UAH to produce washing machines in a week. It costs more to produce washing machines per week, and the cost difference, divided by , is the average increase in cost per one washing machine per week:

=average increase in cost.

The limit of ratio as is the marginal cost when washing machines are produced:

=marginal cost.

The marginal cost estimates the cost of producing one unit beyond the production level.

is the revenue from selling washing machines, then

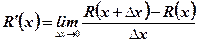=marginal revenue.

The marginal revenue function estimates the increase in revenue that will result from selling one additional unit.

If is profit from selling washing machines, then

= marginal profit.

Дата добавления: 2015-10-23