Методи оцінки параметрів кривих зростання

Параметри поліноміальних кривих оцінюються, як правило, МНК. Цей метод призводить до для визначення невідомих параметрів кривих.

Для полінома першого степеня система нормальних рівнянь матиме вигляд:

(13.9)

Аналогічна система для полінома другого степеня :

(13.10)

Для полінома третього степеня :

(13.10)

Або ж, якщо поліноміальну модель звести до лінійного вигляду і записати в матричному вигляді, оцінки параметрів можна знайти за формулою, запропонованою в п. 5.4.

Параметри експоненціальних і -подібних кривих знаходяться більш складними методами.

Модель простої експоненти 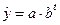з допомогою логарифмування та заміни змінних приводять до лінійного виду, що дозволяє використати для оцінки параметрів МНК. Алгоритм детально описано в п. 4.

При визначенні параметрів кривих росту, що мають асимптоти (модифікована експонента, крива Гомперця, логістична крива), використовують наближені методи: метод трьох точок, метод трьох сум та ін.

Розглянемо метод трьох точок.

Припустимо, що дані є доступними у період і що функція має вигляд модифікованої експоненти:

Алгоритм методу трьох точок

1. Розділити дані на три підмножники, однакові за кількістю елементів.

Точніше:

а) якщо вся кількість елементів без залишку ділиться на 3, тобто , маємо три підмножини з кількістю елементів у кожній: ;

б) якщо , то кількість елементів входить до 2–ої, а множини 1 та 3 складатимуться з елементів;

в) якщо , тоді входить до II множини, а до I, і до III множин.

2. Обчислити значення медіан у 3-х під множниках: .

3. Розв’язання системи 3-х рівнянь (нелінійних) з трьома невідомими:

, (1)

, (2)

, (3)

Виходячи з того, що рівняння є нелінійними, систему можна розв’язати таким чином:

а) спочатку визначити різницю між рівняннями (3) та (2) і між рівняннями (2) та (1):

(4)

(5)

б) поділити почленно рівняння (4) на рівняння (5), позначивши :

в) визначивши 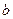, повертаємося до (4):

Отже, при моделюванні економічної динаміки, заданої часовим рядом, шляхом згладжування вихідного ряду, визначення наявності тренду, відбору однієї або декількох кривих росту та визначення їх параметрів у разі наявності тренда отримують одну або кілька трендових моделей для вихідного часового ряду. Постає питання, наскільки ці моделі близькі до економічної реальності, відображеної в часовому ряду, наскільки обґрунтовано застосування цих моделей для аналізу та прогнозування досліджуваного економічного явища.

Дата добавления: 2015-10-23