
Читайте также:
|
Нагрев производится насыщенным водяным паром при абсолютном давлении 0,45 МПа.
При расчете выбран кожухотрубчатый теплообменник, где греющий пар идет в межтрубное пространство, а исходная смесь в трубное. Для межтрубного пространства принят индекс «1», а для трубного – «2».
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 0ХБ2.1.24.030000ПЗ |
Температурная схема:
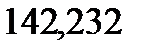 –
– 
20 97,745


где  и
и 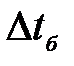 - меньшая и большая разность температур, оС.
- меньшая и большая разность температур, оС.
Средняя разность температур:

| (3.78) |
После подстановки значений:

Средняя температура питания:

| (3.79) |

где  - средняя температура питающей смеси, оС.
- средняя температура питающей смеси, оС.
Объемный расход питающей смеси:

| (3.80) |
где 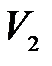 - объемный расход питающей смеси, м3/с;
- объемный расход питающей смеси, м3/с;
 - плотность исходной смеси при средней температуре, кг/м3.
- плотность исходной смеси при средней температуре, кг/м3.
Плотность питающей смеси:

| (3.81) |
где  и
и  - плотности компонентов при средней температуре питания равные 831,9 кг/м3 [1] и 824,9 кг/м3 [1].
- плотности компонентов при средней температуре питания равные 831,9 кг/м3 [1] и 824,9 кг/м3 [1].
После подстановки значения плотность питающей смеси равна:

Объемный расход питающей смеси по формуле (3.80):

Расход теплоты на нагрев питающей смеси с учетом 5% потерь:

| (3.82) |
где  - средняя удельная теплоемкость питающей смеси, Дж/(кг.К);
- средняя удельная теплоемкость питающей смеси, Дж/(кг.К);
 и
и 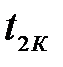 - начальная и конечная температура питания, равные 20 оС и 97,745 оС.
- начальная и конечная температура питания, равные 20 оС и 97,745 оС.
Средняя удельная теплоемкость питающей смеси:

| (3.83) |
где  и
и  - удельные теплоемкости компонентов смеси равные, 1889 Дж/(кг.К) [1] и 1789 Дж/(кг.К) [1].
- удельные теплоемкости компонентов смеси равные, 1889 Дж/(кг.К) [1] и 1789 Дж/(кг.К) [1].

По формуле (3.82) расход теплоты равен:
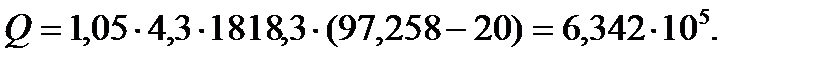
Расход греющего пара с учетом массовой доли сухого воздуха в паре:

| (3.84) |
где  - удельная теплота конденсации водяного пара, равная 2142,8.103 Дж/кг [1];
- удельная теплота конденсации водяного пара, равная 2142,8.103 Дж/кг [1];
 - расход греющего пара, кг/с.
- расход греющего пара, кг/с.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 0ХБ2.1.24.030000ПЗ |

Максимальная величина площади поверхности теплообмена определяется из минимальное значение коэффициента теплопередачи для случая теплообмена от конденсирующегося водяного пара к органическим жидкостям Кмин=120 Вт/(м2.К) [1].
Максимальная величина площади теплообмена:
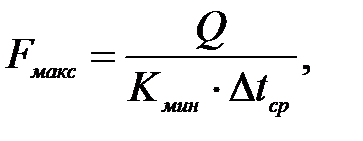
| (3.85) |
где 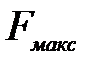 - максимальная площадь поверхности теплообмена, м2.
- максимальная площадь поверхности теплообмена, м2.

Для обеспечения турбулентного течения питающей смеси при Re2>10000 скорость в трубах должна быть больше  :
:

| (3.86) |
где  - динамический коэффициент вязкости питающей смеси, Па.с;
- динамический коэффициент вязкости питающей смеси, Па.с;
 - внутренний диаметр труб, равный 0,021 м [1].
- внутренний диаметр труб, равный 0,021 м [1].
Динамический коэффициент вязкости питания равен:

| (3.87) |
где  и
и  - динамические коэффициенты вязкости компонентов смеси, равные 0,373.10-3 Па.с [1] и 0,367.10-3 Па.с [1].
- динамические коэффициенты вязкости компонентов смеси, равные 0,373.10-3 Па.с [1] и 0,367.10-3 Па.с [1].

По формуле (3.86) скорость равна:

Число труб 25х2 мм, обеспечивающих объемный расход питающей смеси при Re2>10000:

| (3.88) |

Основными условиями для выбора теплообменника являются n<n/ и
F<  м2.
м2.
Данному условию удовлетворяет теплообменник с линзовым компенсатором, диаметром кожуха 400, длиной труб 3 м [2].
Критерий Рейнольдса для трубного пространства:

| (3.89) |
где  - число труб на один ход в выбранном теплообменнике.
- число труб на один ход в выбранном теплообменнике.
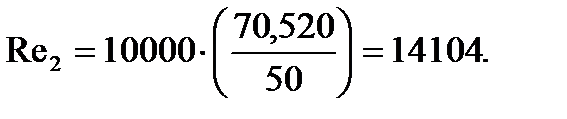
Критерий Прандтля при средней температуре питания:

| (3.90) |
где  - коэффициент теплопроводности питающей смеси, Вт/(м.К).
- коэффициент теплопроводности питающей смеси, Вт/(м.К).
Коэффициент теплопроводности питающей смеси:

| (3.91) |
где  и
и 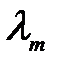 - коэффициенты теплопроводности компонентов питающей смеси средней температуре, Вт/(м.К).
- коэффициенты теплопроводности компонентов питающей смеси средней температуре, Вт/(м.К).
Коэффициенты теплопроводности при средней температуре питающей смеси:

| (3.92) |

| (3.93) |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 0ХБ2.1.24.030000ПЗ |


Коэффициент теплопроводности питающей смеси по формуле (3.91) равен:
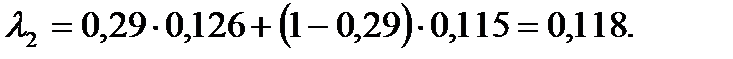
По формуле (3.90) критерий Прандтля равен:

Критерий Нуссельта равен:

| (3.94) |
Отношение  равно 1,07 после чего будет проверено. Значение коэффициента
равно 1,07 после чего будет проверено. Значение коэффициента  принимается равным 1.
принимается равным 1.

Коэффициент теплоотдачи для питающей смеси:

| (3.95) |
где 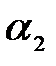 - коэффициент теплоотдачи для питающей смеси, Вт/(м2.К).
- коэффициент теплоотдачи для питающей смеси, Вт/(м2.К).
Примем разность между температурой стенки и температурой конденсации равной  =4,56 оС.
=4,56 оС.
Коэффициент теплоотдачи от греющего пара к стенке:

| (3.96) |
где 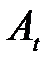 - Функция для воды, равная 7442 [1];
- Функция для воды, равная 7442 [1];
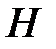 - Высота труб, м;
- Высота труб, м;
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 0ХБ2.1.24.030000ПЗ |
 - разность между температурой стенки и температурой конденсации, оС;
- разность между температурой стенки и температурой конденсации, оС;
 - коэффициент теплоотдачи при конденсации водяного пара на пучке труб, Вт/(м2.К).
- коэффициент теплоотдачи при конденсации водяного пара на пучке труб, Вт/(м2.К).
После подстановки значений коэффициент теплоотдачи равен:

Тепловая проводимость со стороны греющего пара 1/rзагр.1=5800 Вт/(м2.К) [1], со стороны питающей смеси 1/rзагр.2=5800 Вт/(м2.К) [1]. Коэффициент теплопроводности стали  =46,5 Вт/(м2.К) [1].
=46,5 Вт/(м2.К) [1].
Сумма термических сопротивлений стенки и стали:

| (3.97) |
где  - толщина стенки трубы, м;
- толщина стенки трубы, м;
 - сумма термических сопротивления со стороны загрязнений стенки и стали, (м2.К)/Вт.
- сумма термических сопротивления со стороны загрязнений стенки и стали, (м2.К)/Вт.

Коэффициент теплопередачи равен:

| (3.98) |
где  - коэффициент теплопередачи, Вт/(м2.К).
- коэффициент теплопередачи, Вт/(м2.К).
После подстановки значений в формулу (3.98) коэффициент теплопередачи равен:

Поверхностная плотность теплового потока равна:

| (3.99) |
где  - поверхностная плотность теплового потока, Вт/м2.
- поверхностная плотность теплового потока, Вт/м2.
После подстановки значений поверхностная плотность равна:

Проверка ранее принятой  :
:

| (3.100) |
После подстановки значений:

Найденная температура практически равна принятой:
Разность между температурой стенки и средней температурой исходной смеси в оС:

| (3.101) |

Температура стенки в оС равна:

| (3.102) |

Критерий Прандтля для питания при температуре стенки:

| (3.103) |
где  - средняя удельная теплоемкость питающей смеси при температуре стенки, Дж/(кг.К);
- средняя удельная теплоемкость питающей смеси при температуре стенки, Дж/(кг.К);
 - динамический коэффициент вязкости питающей смеси при температуре стенки, Па.с;
- динамический коэффициент вязкости питающей смеси при температуре стенки, Па.с;
 - коэффициент теплопроводности питающей смеси при температуре стенки, Вт/(м.К).
- коэффициент теплопроводности питающей смеси при температуре стенки, Вт/(м.К).
Средняя удельная теплоемкость питания при температуре стенки:

| (3.104) |
где 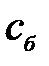 и
и  - удельные теплоемкости компонентов смеси при температуре стенки, равные 2220,7 Дж/(кг.К) [1] и 1939,97 Дж/(кг.К) [1].
- удельные теплоемкости компонентов смеси при температуре стенки, равные 2220,7 Дж/(кг.К) [1] и 1939,97 Дж/(кг.К) [1].
После подстановки значений в формулу (3.104) теплоёмкость равна:

Динамический коэффициент вязкости при температуре стенки:
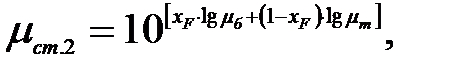
| (3.105) |
где  и
и  - динамические коэффициенты вязкости компонентов смеси при температуре стенки, равные 0,184.10-3 Па.с [1] и 0,204.10-3 Па.с [1].
- динамические коэффициенты вязкости компонентов смеси при температуре стенки, равные 0,184.10-3 Па.с [1] и 0,204.10-3 Па.с [1].
После подстановки значений в формулу (3.105) вязкость равна:
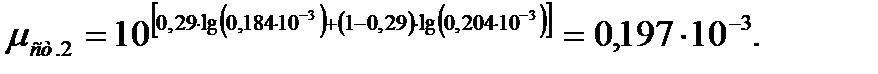
Коэффициент теплопроводности при температуре стенки равен:

| (3.106) |
Коэффициенты теплопроводности компонентов при температуре стенки равны 0,106 Вт/(м.К) [1], 0,094 Вт/(м.К) [1].
Коэффициент теплопроводности после подстановки значений в формулу (3.106) равен:

Критерий Прандтля из формулы (3.103) равен:

Расчетное значение соотношения  .
.
Было принято  . Принятое и рассчитанное значения отличаются не более чем на 10 %, расчет принять верным.
. Принятое и рассчитанное значения отличаются не более чем на 10 %, расчет принять верным.
Площадь поверхности теплопередачи с запасом 10% равна:

| (3.107) |
где  - расчетная площадь поверхности теплообмена, м2.
- расчетная площадь поверхности теплообмена, м2.
Площадь поверхности после подстановки значений равна:

Теоритическая площадь поверхности теплообмена:

| (3.108) |
где  - внешний диаметр труб, м;
- внешний диаметр труб, м;
 - площадь поверхности теплообмена, м2.
- площадь поверхности теплообмена, м2.
После подстановки значений площадь равна:

Запас площади теплообмена в %:

| (3.109) |
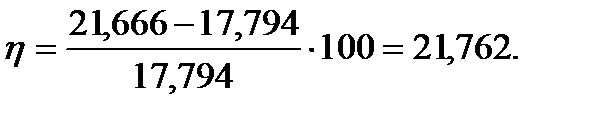
Тепловой запас почти 21,8 % - принимают теплообменники с линзовым компенсатором типа (ТК).
Принимают один двухходовой теплообменник с линзовым компенсатором с диаметром кожуха 400 мм, числом труб 100, длиной труб L=3 м.
Дата добавления: 2015-10-30; просмотров: 142 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Гидравлическое сопротивление тарелок колонны | | | Холодильник дистиллята |