Коэффициенты массопередачи и высота колонны

Вязкость паров чистого бензола при 88,931 ^оС 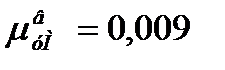мПа∙с [4].

Вязкость паров чистой толуола при 102,692 ^оС 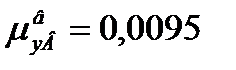мПа∙с [4].

Вязкость паров чистого бензола при 92,234 ^оС 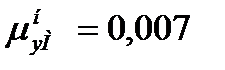мПа∙с [4].

Вязкость паров чистой толуола при 104,324 ^оС 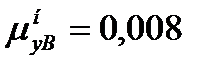мПа∙с [4].

Вязкость газообразной смеси определяется по формуле

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

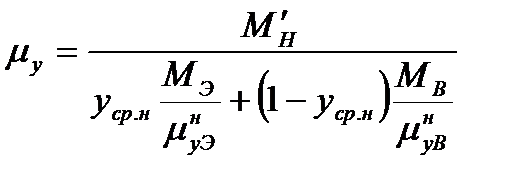. (3.42)

Для верхней части колонны:

.

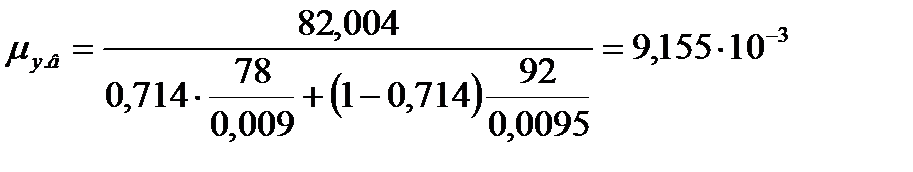Для нижней части колонны:

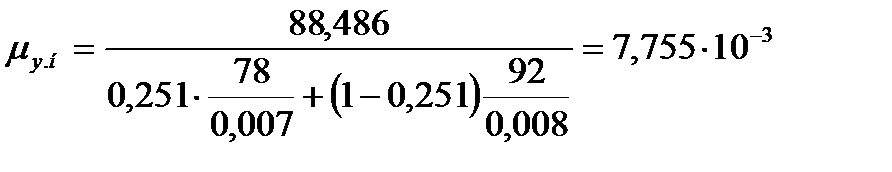
Динамический коэффициент вязкости жидкого бензола при 20 ^оС 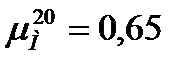мПа∙с.

Динамический коэффициент вязкости жидкой толуола при 20 ^оС

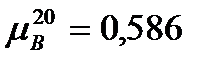мПа∙с.

Динамический коэффициент вязкости жидкой смеси для верхней части колонны при 20 ^оС по формуле (3.28) равен

.

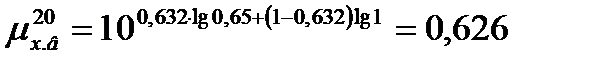Динамический коэффициент вязкости жидкой смеси для нижней части колонны при 20 ^оС по формуле (3.28) равен

.

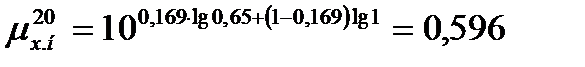Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

Коэффициент диффузии в жидкости при 20 ^оС определяется по соотношению

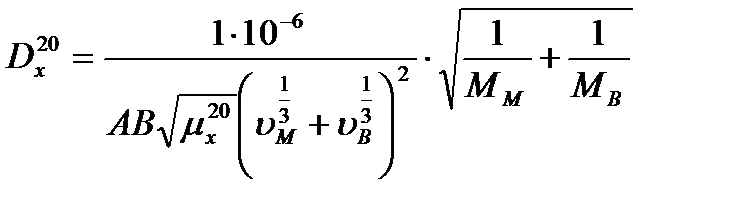, (3.43)

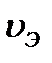где и 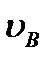- мольные объёмы компонентов бинарной смеси, см³/моль;

А и В – коэффициенты, зависящие от свойств компонентов бинарной смеси.

Для бензола коэффициент 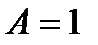[4].

Для толуола коэффициент 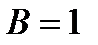[4].

Мольный объём бензола 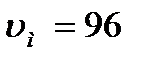[3]. Мольный объём толуола 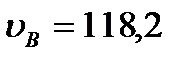[3].

Коэффициент диффузии в жидкости при 20 ^оС для верхней части колонны по формуле (3.43) равен

.

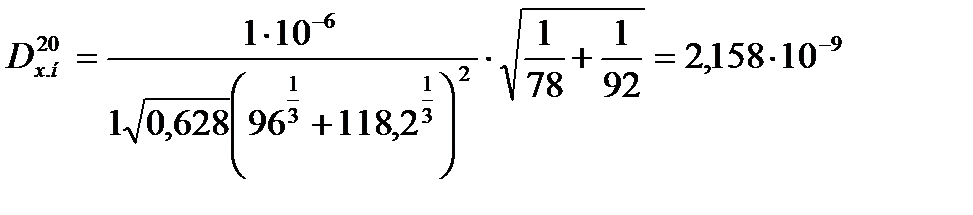
Коэффициент диффузии в жидкости при 20 ^оС для нижней части колонны по формуле (3.43) равен

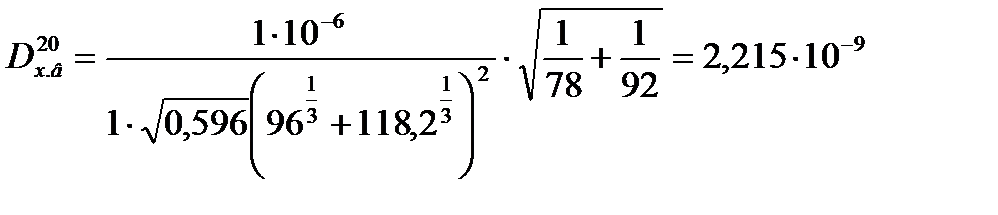
Коэффициент диффузии в жидкости при температуре отличной от 20 ^оС связан с коэффициентом диффузии в жидкости при 20 ^оС следующим соотношением

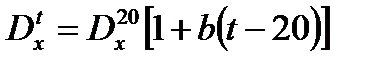, (3.44)

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

где 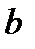- температурный коэффициент.

Температурный коэффициент может быть определён по эмпирической формуле

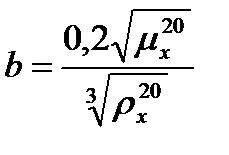, (3.45)

где 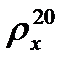- плотность жидкости при 20 ^оС, кг/м³.

Плотность жидкого бензола при 20 ^оС .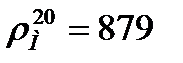

Плотность жидкой толуола при 20 ^оС .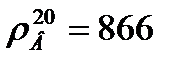

Плотность жидкости для верхней части колонны при 20 ^оС по формуле (3.26) равна

.

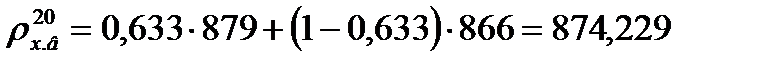Плотность жидкости для нижней части колонны при 20 ^оС по формуле (3.26) равна

.

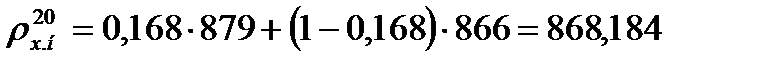Температурный коэффициент для верхней части колонны по формуле (3.45) равен

.

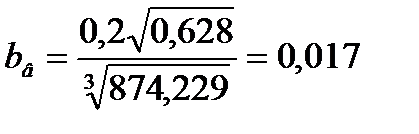Температурный коэффициент для нижней части колонны по формуле (3.45) равен

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

.

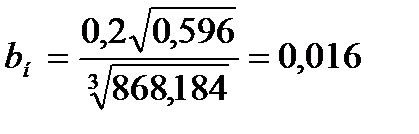Коэффициент диффузии в жидкости для верхней части колонны при 88,931 ^оС по формуле (3.44) равен

.

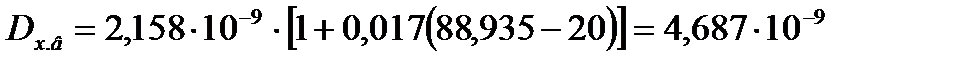Коэффициент диффузии в жидкости для нижней части колонны при 102,692 ^оС по формуле (3.44) равен

.

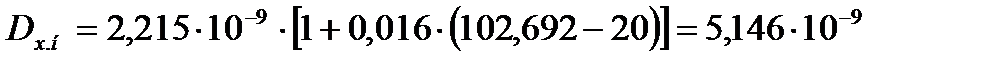Коэффициент диффузии в паровой фазе может быть вычислен по уравнению

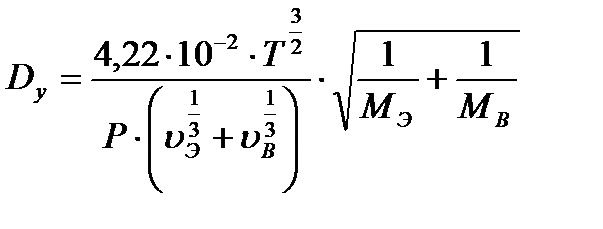, (3.46)

где 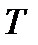- температура, К;

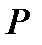- абсолютное давление, Па. Коэффициент диффузии в паровой фазе для верхней части колонны при 92,234 ^оС по формуле (3.46) равен

.

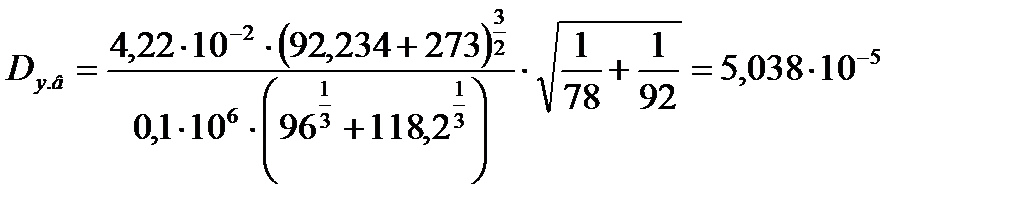Коэффициент диффузии в паровой фазе для нижней части колонны при 104,324 ^оС по формуле (3.46) равен

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

.

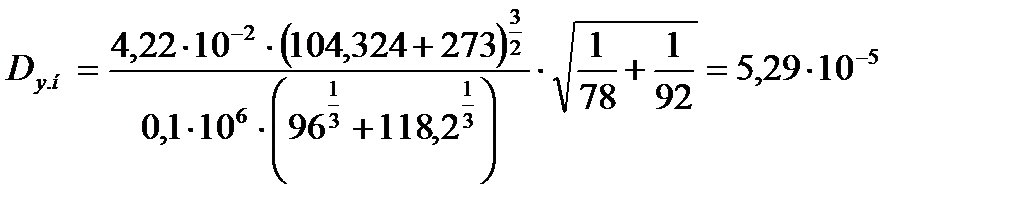Коэффициенты массоотдачи в жидкой фазе определяются по соотношению

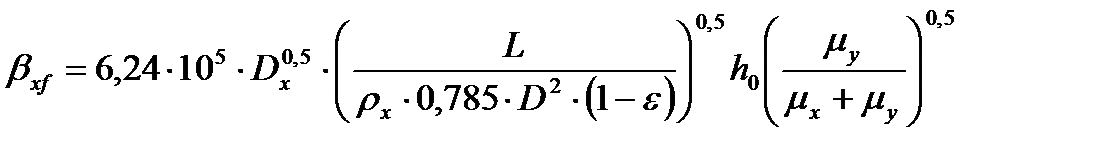(3.47)

Коэффициент массоотдачи в жидкой фазе для верхней части колонны по формуле (3.47) равен

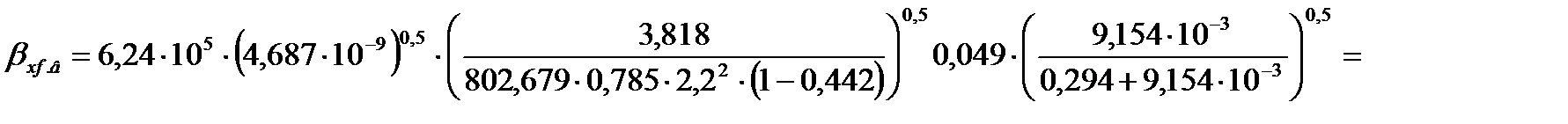=0,017

Коэффициент массоотдачи в жидкой фазе для нижней части колонны по формуле (3.47) равен

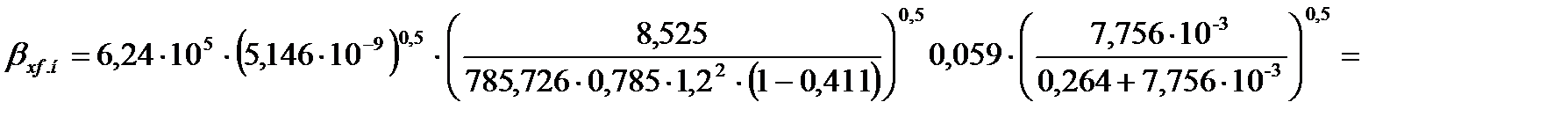
=0,031

Коэффициенты массоотдачи в паровой фазе определяются по соотношению

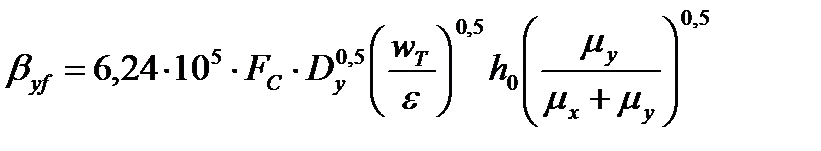. (3.48)

Коэффициент массоотдачи в паровой фазе для верхней части колонны по формуле (3.48) равен

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

.

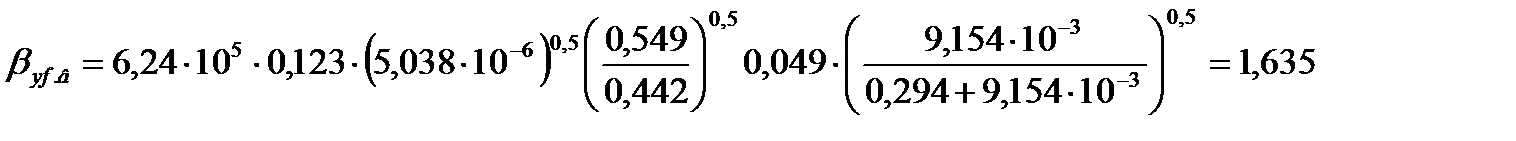Коэффициент массоотдачи в паровой фазе для нижней части колонны по формуле (3.48) равен

.

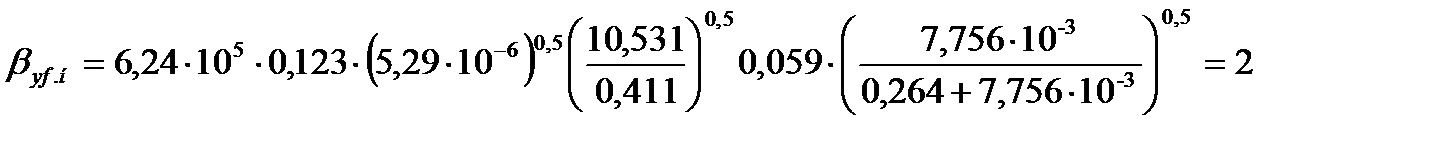Пересчитаем коэффициенты массоотдачи на кмоль/(м²∙с) по соотношению

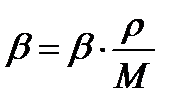. (3.49)

Для верхней части колонны коэффициенты массотдачи в жидкой и паровой фазах по формуле (3.49) равны

,

.

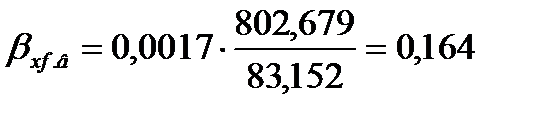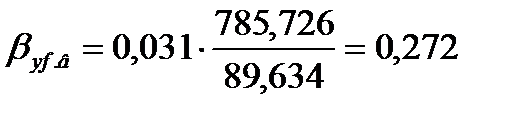Для нижней части колонны коэффициенты массотдачи в жидкой и паровой фазах по формуле (3.49) равны

,

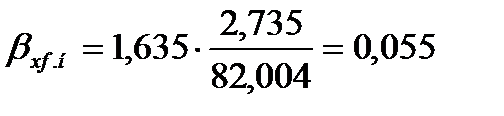Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

.

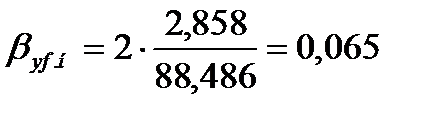Коэффициенты массоотдачи, рассчитанные по средним значениям скоростей и физических свойств паровой и жидкой фаз, постоянны для верхней и нижней частей колонны. В то же время коэффициент массопередачи – величина переменная, зависящая от кривизны линии равновесия, т.е. от коэффициента распределения. Поэтому для определения данных, по которым строится кинетическая линия, необходимо вычислить несколько значений коэффициента массопередачи в интервале изменения состава жидкости от 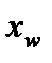до .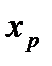

Пусть 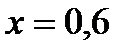. Коэффициент распределения компонента по фазам (тангенс угла наклона равновесной линии в этой точке) .

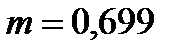Коэффициент массопередачи вычисляется по формуле

Содержание низкокипящего компонента 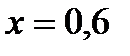соответствует верхней части колонны, поэтому коэффициент массопередачи необходимо рассчитывать по коэффициентам массоотдачи для верхней части колонны.

Коэффициент массопередачи по формуле (3.50) равен

.

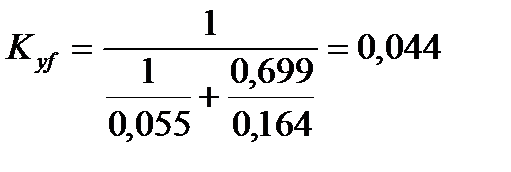Общее число единиц переноса на тарелку определяется по уравнению

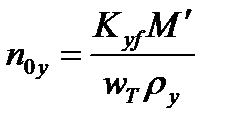, (3.51)

.

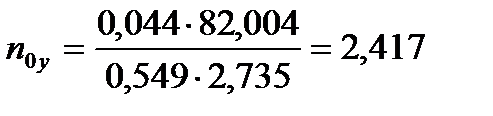Локальная эффективность определяется по уравнению

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

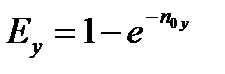, (3.52)

.

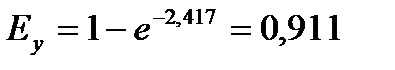Фактор массопередачи для верхней части колонны определяется по уравнению

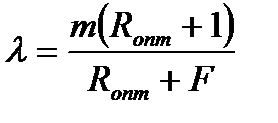, (3.54)

Фактор массопередачи по формуле (3.53) равен

.

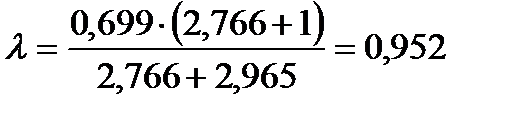Долю байпасирующей жидкости 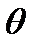примем равной 0,1.

Число ячеек полного перемешивания определяется по уравнению

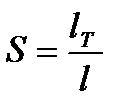, (3.56)

где 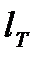- длина пути жидкости на тарелке, м;

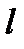- длина пути, соответствующая одной ячейке перемешивания, м.

Длину пути, соответствующую одной ячейке перемешивания примем равной 0,35 м.

Длину пути жидкости на тарелке определим по формуле

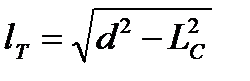, (3.57)

.

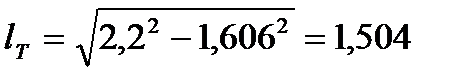Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

Число ячеек полного перемешивания по формуле (3.56) равно

.

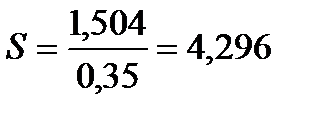Относительный унос жидкости 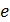в тарельчатых колоннах определяется в основном скоростью пара, высотой сепарационного пространства и физическими свойствами жидкости и пара. В настоящее время нет надежных зависимостей, учитывающих влияние физических свойств потоков на унос, особенно для процессов ректификации. Для этих процессов унос можно оценить с помощью графических данных. По этим данным унос на тарелках является функцией комплекса 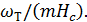Коэффициент m, учитывающий влияние на унос физических свойств жидкости и пара определяют по уравнению:

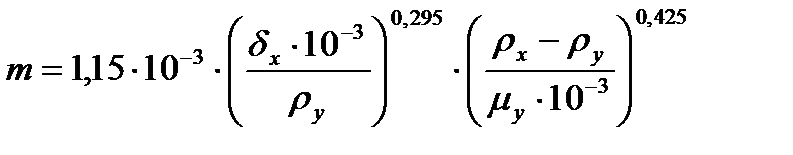(3.58)

Для верней части колонны:

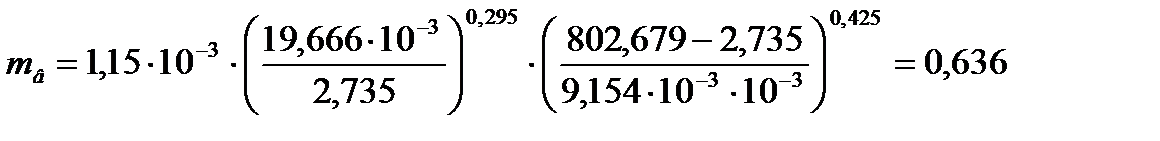
Для нижней части колонны:

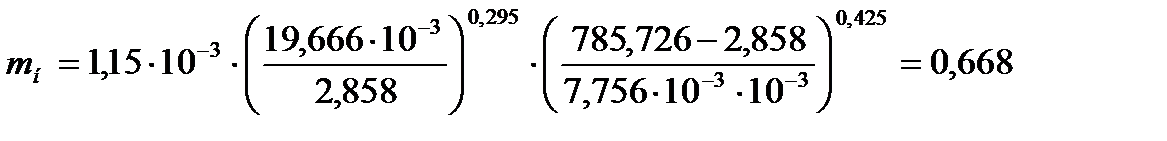
Высота сепарационного пространства 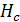равна:

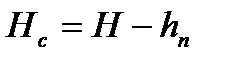(3.59)

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

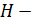где межтарельчатое расстояние, равное 0,5 м;

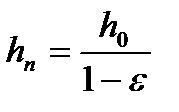высота барботажного слоя (пены), м.

Определим высоту барботажного слоя:

Для верхней части колонны:

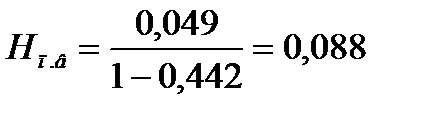
Для нижней части колонны:

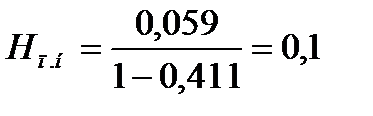
Высота сепарационного пространства равна:

Для верхней части колонны:

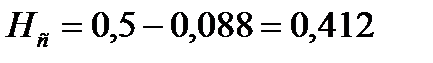
Для нижней части колонны:

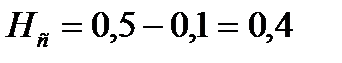
Следовательно, комплекс 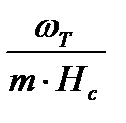будет равен:

Для верхней части колонны:

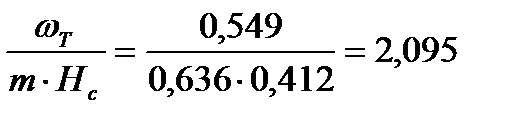
Для нижней части колонны:

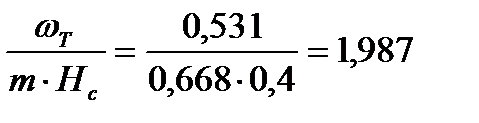
Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

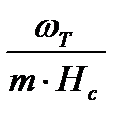При таком значении комплекса унос для верхней части колонны 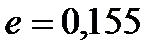, для нижней части колонны 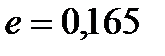. Т. к. относительный унос в верхней и нижней частях колонны различаются незначительно, то примем среднее значение .

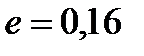Таблица 3.2 Коэффициент В определяется по формуле

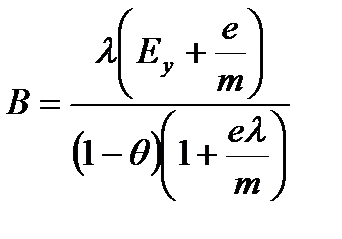, (3.60)

.

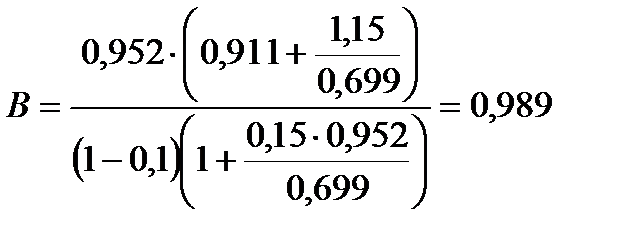Коэффициент 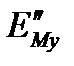определяется по формуле

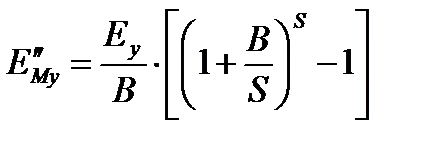, (3.61)

.

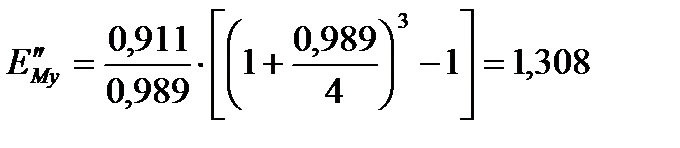Коэффициент 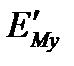определяется по формуле

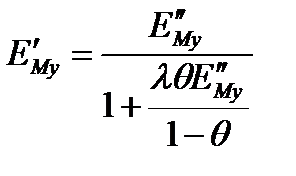, (3.62)

Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

.

Эффективность тарелки по Мэрфри определяется по соотношению

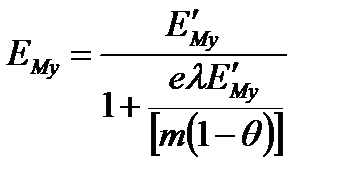, (3.63)

.

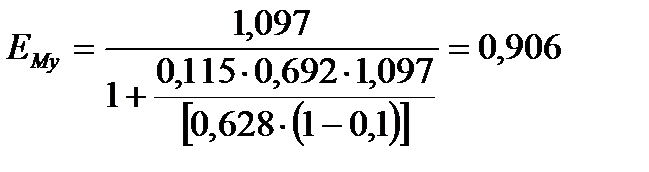Концентрация легкокипящего компонента в паре на выходе из тарелки определяется по соотношению

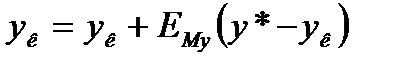, (3.64)

где 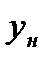- концентрация легкокипящего компонента в паре на входе в тарелку;

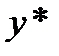- концентрация легкокипящего компонента в паре равновесная с жидкостью на тарелке.

Концентрация легкокипящего компонента в паре на входе в тарелку определяется из рабочей (рисунок) Г.1. При .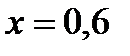

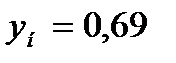Концентрация легкокипящего компонента в паре равновесная с жидкостью на тарелке определяется из равновесной линии (рисунок Г.1). При .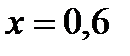

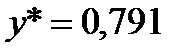Концентрация легкокипящего компонента в паре на выходе из тарелки по формуле (3.64) равна

.

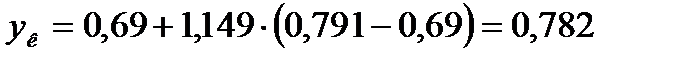Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

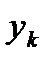Аналогичным образом подсчитаны и для других составов жидкости. Результаты расчётов параметров, необходимых для построения кинетической кривой приведены в таблице 3.2.

Таблица 3.2

Параметр	Нижняя часть колонны	Верхняя часть колонны
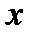
	0,15	0,2	0,25	0,4	0,6	0,8	0,9
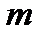
	1,842	1,507	1,289	0,928	0,699	0,572	0,527
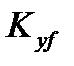
	0,045	0,048	0,049	0,042	0,044	0,046	0,046
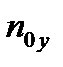
	2,619	2,773	2,883	2,276	2,417	2,502	2,534
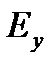
	0,927	0,938	0,944	0,897	0,911	0,918	0,921
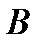
	1,235	1,039	0,909	1,235	0,989	0,848	0,798
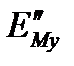
	1,452	1,37	1,317	1,405	1,308	1,254	1,235
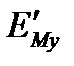
	1,215	1,191	1,172	1,173	1,149	1,131	1,124
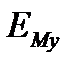
	1,072	1,053	1,039	0,927	0,911	0,9	0,896
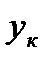
	0,295	0,376	0,442	0,613	0,782	0,905	0,954
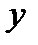
	0,222	0,298	0,374	0,543	0,69	0,837	0,911
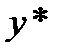
	0,29	0,372	0,439	0,619	0,791	0,912	0,959
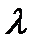
	1,21	0,99	0,847	1,264	0,952	0,779	0,717

Взяв из таблицы 3.2 значения 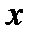и 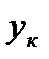строим кинетическую линию в Приложении Е, рисунок Е.1. Графическим построением ступеней изменения концентрации между рабочей и кинетической линиями определяем число действительных тарелок для нижней части колонны 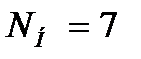и верхней части колонны .

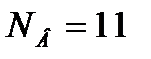Изм.

Лист

№ докум.

Подпись

Дата

Лист

0ХБ2.1.24.030000ПЗ  

Общее число тарелок ректификационной колонны определится соотношением

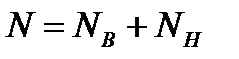, (3.65)

.

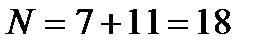Высоту тарельчатой ректификационной колонны определим по формуле

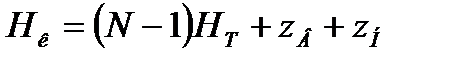, (3.66)

где 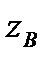- расстояние между верхней тарелкой и крышкой колонны, м;

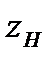- расстояние между днищем колонны и нижней тарелкой, м.

В соответствии с диаметром колонны расстояние между верхней тарелкой и крышкой колонны равно 1 м [1], расстояние между днищем колонны и нижней тарелкой равно 2 м [1].Также в Mathcade рассчитали оптимальное межтарельчатое расстояние Нт=0,5

Общая высота колонны по формуле (3.66) равна

.

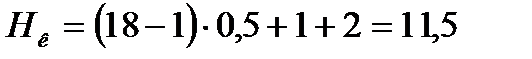Дата добавления: 2015-10-30