|
Читайте также: |
October 29, 2010
Lecturer: K.A. Bukin
Class teachers: A. Arlashin, G. Sharygin, S. Provornikov
Marks will be deducted for insufficient explanation within your answers. Sections A and B will make up 60% and 40% of the exam grade, respectively. Total duration of the exam is 120 min.
SECTION A
Answer SIX of the six questions from this section.
17. Find domain 
of the function 
.
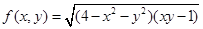Let 
. Is the set 
open or closed? Is it bounded? Explain.
18. Find the limit of the function 
at the origin or show that it does not exist:
.
19. Let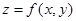 
be a continuously differentiable function everywhere, where 
, 
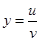. Find the total differential of 
.
20. Find the Hesse matrix of 
. Clearly state Young's theorem if you use it.
21. Find the approximate value of 
. Convert degrees into radians firstly.
22. If the equation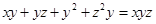 
defines an implicit function 
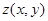near the point 
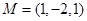find the value of 
at that point in the direction of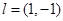 
.
PLEASE TURN OVER
SECTION B
Answer TWO of the two questions from this section.
23. The temperature at each point 
in the room is given by the equation 
. A fly is currently hovering at the point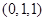 
of the room. Find the rate of change of the temperature 
if the fly moves:
a. in the direction to cool off as rapidly as possible;
b. in the direction parallel to the both the floor (z value is fixed) and the side wall (y value is fixed).
24. Given the system
Does this system define the vector implicit function 
in the neighborhood of the point 
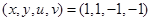? Explain referring to the IFT.
Calculate 
, 
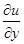and 
at the point (1, 1,-1, -1).
Mathematics for economists
Mock Exam Paper
October 29, 2010
Lecturer: K.A. Bukin
Class teachers: A. Arlashin, G. Sharygin, S. Provornikov
Marks will be deducted for insufficient explanation within your answers. Sections A and B will make up 60% and 40% of the exam grade, respectively. Total duration of the exam is 120 min.
SECTION A
Answer SIX of the six questions from this section.
25. Find domain of the function 
.
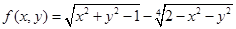Let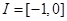 
. Is the set open or closed? Is it bounded? Explain.
26. Find the limit of the function at the origin or show that it does not exist:
.
27. Let 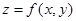be a continuously differentiable function everywhere, where 
, 
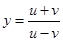. Find the total differential of 
.
28. Find the Hesse matrix of 
. Clearly state Young's theorem if you use it.
29. Find the approximate value of 
. Convert degrees into radians firstly.
30. If the equation 
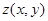defines an implicit function near the point 
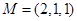find the value of at that point in the direction of 
.
PLEASE TURN OVER
SECTION B
Answer TWO of the two questions from this section.
31. The temperature at each point in the room is given by the equation 
. A fly is currently hovering at the point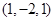 
of the room. Find the rate of change of the temperature if the fly moves:
a. in the direction to warm itself as rapidly as possible;
b. in the direction parallel to the both the floor (z value is fixed) and the side wall (x value is fixed).
32. Given the system
Does this system define the vector implicit function in the neighborhood of the point 
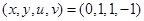? Explain referring to the IFT.
Calculate , 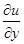and at the point (0, 1,1, -1).
Дата добавления: 2015-10-30; просмотров: 170 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Mathematics for economists | | | Загальна характеристика ДП ПАТ «Київхліб» Хлібокомбінат №11 |