
Читайте также:
|
ВСТУП
В умовах ринкової економіки, коли кожній господарській одиниці треба самостійно ухвалювати рішення, стає необхідним математичний розрахунок. Тому роль математичних методів в економіці постійно зростає.
Економіко-математичне моделювання є галуззю економічної науки, яка вивчає основні принципи та інструментарій постановки економічних задач, побудови їх математичних моделей, методів розв’язування та аналізу економічних задач. Застосування економіко-математичних методів і моделей в економіці дозволяє істотно поліпшити якість планування і отримати додатковий ефект без залучення до виробництва додаткових ресурсів.
Метою курсової роботи є вивчення методів розв’язування різних типів економічних задач. У роботі розглядаються основні методи розв’язування, аналізу та використання задач на знаходження екстремуму функції на множині допустимих варіантів у широкому спектрі теоретико-економічних та практичних проблем.
ЗАВДАННЯ 1
Побудувати на площині множину (багатокутник) розв’язків системи лінійних обмежень-нерівностей і графічним методом знайти найбільше та найменше значення цільової функції в цьому багатокутнику (x1³0, x2³0).
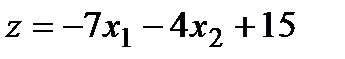

Розв’язання завдання.
Дана задача лінійного програмування містить в собі лише дві змінні, тому вона може бути розв’язана за допомогою графічного методу, що базується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування [3].
Першим кроком необхідно побудувати на площині прямі лінії, рівняння яких можна знайти, замінивши знаки нерівностей в обмеженнях задачі на знаки рівностей. У результаті отримаємо наступні графіки прямих (рис. 1.1).
Наступним кроком визначаємо півплощини, що відповідають кожному обмеженню задачі. Оскільки у даному випадку x1³0 та x2³0, то обмежимося першим квадрантом системи координат. Для того, щоб визначити необхідну півплощину, необхідно взяти будь-яку точку на площині та перевірити, чи задовольняють її координати задане обмеження. Якщо точка задовольняє обмеження, то дана півплощина і є геометричним відображенням нерівності. Якщо ж ні, то геометричним зображенням нерівності є інша півплощина. Півплощини розв’язків зображені штриховкою на рисунку 1.1.
Дана фігура є обмеженою з усіх боків і тому вона набуває як мінімального значення так і максимального
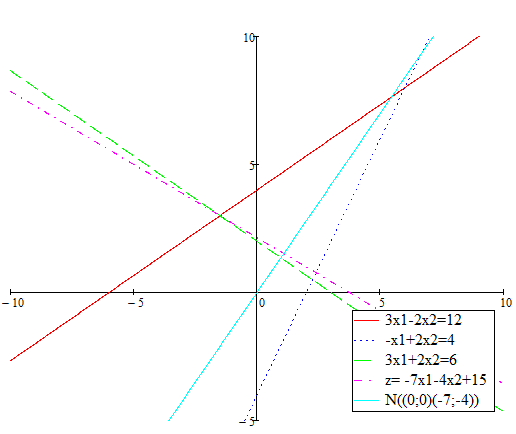
Рисунок 1.1 – Графічне зображення розв’язку задачі лінійного програмування
Далі будуємо вектор, що задає напрям зростання значень цільової функції задачі. У даному випадку це вектор  = (-7; -4). Координати цього вектора – це коефіцієнти при змінних цільової функції. Цей вектор виходить із початку координат і проходить через точку (-7; -4).
= (-7; -4). Координати цього вектора – це коефіцієнти при змінних цільової функції. Цей вектор виходить із початку координат і проходить через точку (-7; -4).
Наступним кроком будуємо пряму с1х1 + с2х2 = const, перпендикулярну вектору  . Для даної задачі побудуємо пряму -7х1-4х2+15=0. Пересуваючи пряму паралельно самій собі у напрямі вектора
. Для даної задачі побудуємо пряму -7х1-4х2+15=0. Пересуваючи пряму паралельно самій собі у напрямі вектора 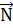 , знайдемо найвищу (А) й найнижчу (В) точку багатокутника.
, знайдемо найвищу (А) й найнижчу (В) точку багатокутника.
Координати точки А є розв’язком системи рівнянь:

| (1.1) |

| (1.2) |
Із даної системи рівнянь х1 = 8, х2 =6. Отже, min Z = -65.
Координати точки В також є розв’язком системи рівнянь:
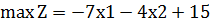
| (1.3) |

| (1.4) |
Із даної системи рівнянь х1 = 0.5, х2 =2.25. Отже, max Z = 2.5.
Для того, щоб перевірити правильність вирішення поставленої задачі, скористаємося пакетом MathCad. Для знаходження максимуму та мінімуму функції використаємо функції Maximize та Minimize.
Результати розрахунків представлені на рис. 1.2, 1.3.
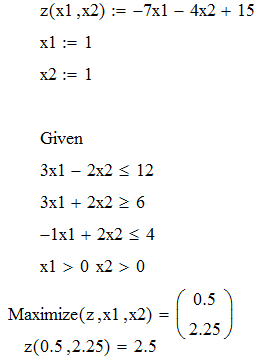
Рисунок 1.2 – Розрахунок максимуму функції
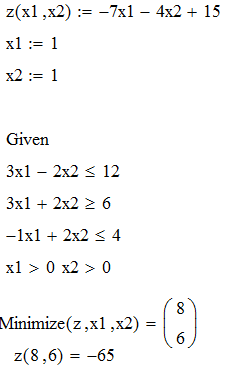
Рисунок 1.3 – Розрахунок мінімуму функції
ЗАВДАННЯ 2
Симплексним методом знайти розв’язок задачі лінійного програмування.
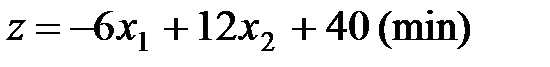

Розв’язання завдання.
Для розв’язання задач лінійного програмування, окрім графічного методу, також використовують симплекс-метод, який є більш універсальним, так як за його допомогою можна шукати оптимальні плани задач лінійного програмування, що у своєму складі мають більше, ніж дві змінні. Процес розв’язання задачі симплекс-методом має ітераційний характер: обчислювальні процедури одного й того самого типу повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або буде з’ясовано, що його не існує [3].
Щоб розв’язати поставлену задачу лінійного програмування, перш за все необхідно записати дану задачу в канонічному вигляді. Для цього перейдемо від обмежень-нерівностей до рівнянь, увівши додаткові змінні в обмеження. Система рівнянь матиме вигляд:
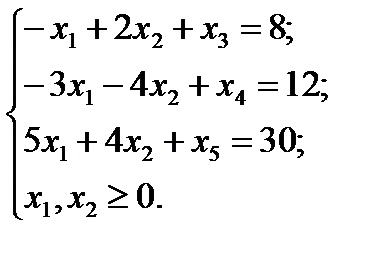 (2.1)
(2.1)
У цільовій функції задачі додаткові змінні мають коефіцієнти нуль.
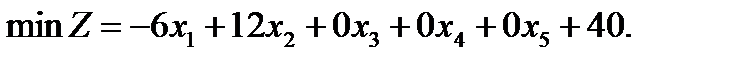
| (2.2) |
Далі необхідно записати задачу у векторній формі. Опорний план задачі утворюють m одиничних лінійно незалежних векторів, що становлять базис m-вимірного простору (m – кількість обмежень у задачі лінійного програмування).
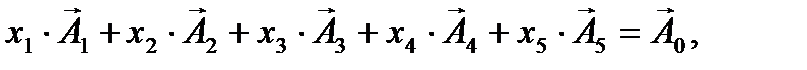
| (2.3) |
де
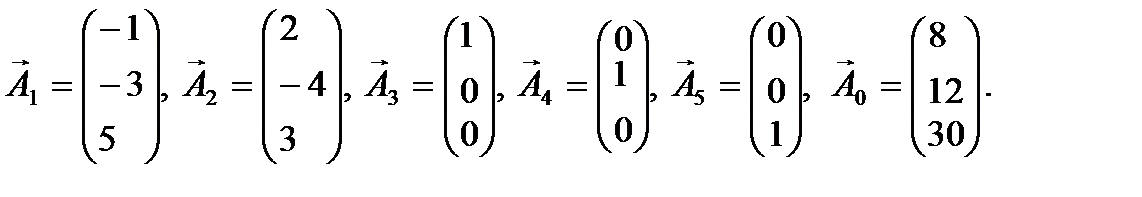 (2.4) (2.4)
|
Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні – вільними. Їх прирівнюємо до нуля та з кожного обмеження задачі визначаємо значення базисних змінних. У такий спосіб отримуємо початковий опорний план задачі лінійного програмування. У даному випадку, прирівнявши вільні змінні до нуля, з кожного обмеження дістанемо наступні значення базисних змінних:

| (2.5) |
Згідно з визначеними 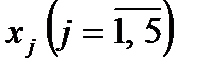 векторна форма запису системи обмежень цієї задачі матиме вигляд:
векторна форма запису системи обмежень цієї задачі матиме вигляд:
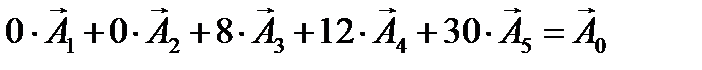
| (2.6) |
Другим кроком будуємо симплексну таблицю для перевірки оптимальності опорного плану.
Отже, перший опорний план задачі матиме вигляд, представлений у таблиці 2.1.
Таблиця 2.1 – Перша симплексна таблиця
| Базисні змінни | Вільні члени | X1 | X2 | |
| X3 | -1 | |||
| X4 | -3 | -4 | ||
| X5 | 5 | |||
| F | -6 |
Так як у стовпці вільних членів немає від’ємних елементів, то знайдено допустиме рішення. Так як у рядку F є від’ємні елементи, то отримане рішення не оптимально. Для визначення ведучого стовпчика знайдемо максимальний по модулю від’ємний елемент у рядку F (-6). А ведучий рядок тій, у якого найменше позитивне відношення вільного члена до відповідного елементу ведучого стовпця.
Усі елементи наступної симплексної таблиці розраховують за правилом прямокутника. Щоб визначити будь-який елемент нової таблиці за цим правилом, необхідно в попередній симплексній таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:
1 – розв’язувальний елемент;
2 – число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;
3 та 4 – елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.
Необхідний елемент нової симплексної таблиці визначаємо за формулою 2.7.
 (2.7) (2.7)
|
Таблиця 2.2 – Друга симплексна таблиця
| Базисні змінни | Вільні члени | X1 | X4 | |
| X3 | 0,2 | 2,6 | ||
| X2 | 0,6 | -2,2 | ||
| X5 | 0,2 | 0,6 | ||
| F | 1,2 | 15,6 |
Так як у рядку F немає від’ємних елементів, то отримане рішення оптимально.
Отже, оптимальний план задачі знайдено. Він має наступний вигляд:
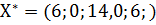 (2.8) (2.8)
| |
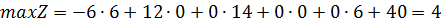 (2.9) (2.9)
|
Перевіримо правильність виконання поставленої задачі за допомогою MathCad.
Результат виконання поставленої задачі представлений на рисунку 2.1.
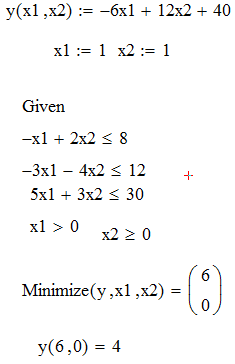
Рисунок 2.1 – Вирішення поставленої задачі у MathCad
ЗАВДАННЯ 3
Побудувати двоїсту задачу до заданої задачі лінійного програмування. Визначити оптимальні плани прямої та двоїстої задач.
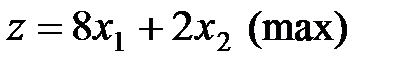
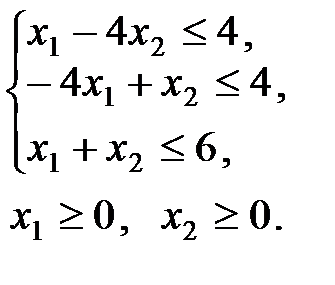
Розв’язання завдання.
Кожній задачі лінійного програмування відповідає двоїста, що формується за допомогою певних правил безпосередньо з умови прямої задачі.
Для побудови двоїстої задачі користуються наступними правилами.
1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.
2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, кількість обмежень дорівнює кількості невідомих прямої задачі.
3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення, то цільова функція двоїстої задачі – на визначення найменшого значення, і навпаки.
4. Коефіцієнтами при змінних в цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.
5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних в цільовій функції прямої задачі [3].
Перш за все зведемо пряму задачу до стандартного вигляду. Для цього другу, третю та четверту нерівність в системі обмежень помножимо на (-1), щоб змінити знак нерівності на протилежний. Пряма задача матиме наступний вигляд:
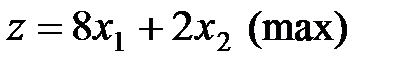 (3.1) (3.1)
| |
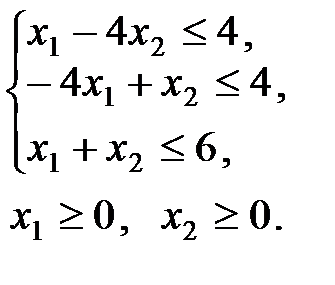 (3.2) (3.2)
|
Далі складемо двоїсту задачу за наведеними вище правилами:
 (3.3) (3.3)
| |
 (3.4) (3.4)
|
Оскільки дані задачі є симетричними (обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень), то будь-яку із них можна розв’язати симплекс-методом. Розв’яжемо двоїсту задачу модифікованим симплексним методом.
Перейдемо від системи нерівностей до системи рівнянь. Задача матиме вигляд:
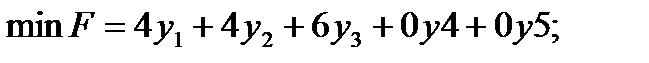 (3.5) (3.5)
| |
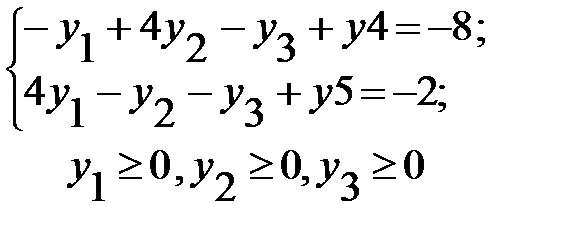 (3.6) (3.6)
|
Запишемо задачу у векторному вигляді:
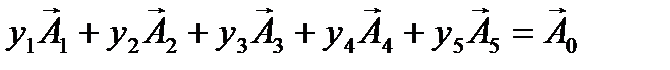 (3.7) (3.7)
| |
Де
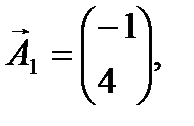 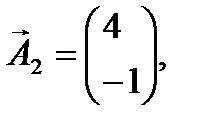 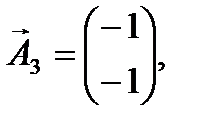 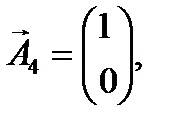 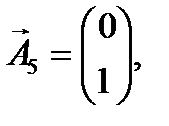 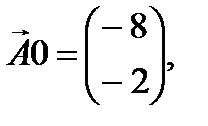 (3.8) (3.8)
|
Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні – вільними. Їх прирівнюємо до нуля та з кожного обмеження задачі визначаємо значення базисних змінних. У такий спосіб отримуємо початковий опорний план задачі лінійного програмування. У даному випадку, прирівнявши вільні змінні до нуля, з кожного обмеження дістанемо наступні значення базисних змінних:
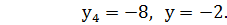
| (3.9) |
Отже, перший опорний план задачі матиме вигляд, представлений у таблиці 3.1.
Таблиця 3.1 – Перша симплексна таблиця задачі
| Базисні змінни | Вільні члени | X1 | X2 | X3 | |
| X4 | -8 | -1 | -1 | ||
| X5 | -2 | -1 | -1 | ||
| F |
Подальше рішення аналогічно завданню 2, далі приведені тількі наступні симплекс-таблиці.
Таблиця 3.2 – Друга симплексна таблиця задачі
| Базисні змінни | Вільні члени | X1 | X2 | X5 | |
| X4 | -1 | -4 | |||
| X3 | -34 | -5 | |||
| F | -32 |
Таблиця 3.3 – Третя симплексна таблиця задачі
| Базисні змінни | Вільні члени | X1 | X4 | X5 | |
| X2 | 1.2 | -0.2 | -1 | 0.2 | |
| X3 | 6.8 | -0.8 | -3 | -0.2 | |
| F | -45.6 | 5.6 | 0.4 |
Отже, як бачимо, всі умови оптимальності у третій симплексній таблиці виконуються. Це значить, що оптимальний план задачі знайдено. Він має наступний вигляд:
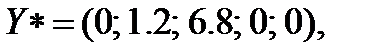
| (3.10) |
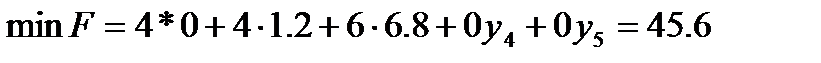
| (3.11) |
Згідно із першою теоремою двоїстості, значення цільових функцій для оптимальних планів задачі дорівнюють одне одному, тому робимо висновок, що оптимальний план прямої задачі існує.
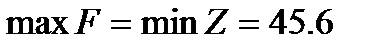
| (3.12) |
Компоненти вектора X* (оптимальний план прямої задачі) визначимо за першою теоремою двоїстості за наступним співвідношенням:

| (3.13) |
де Сбаз – вектор-рядок, що складається з коефіцієнтів цільової функції двоїстої задачі при змінних, які є базисними в оптимальному плані;
D-1 – матриця, обернена до матриці D, складеної з базисних векторів оптимального плану, компоненти яких узято з початкового опорного плану задачі.
Обернена матриця D-1 завжди міститься в останній симплекс-таблиці в тих стовпчиках, де в першій таблиці містилася одинична матриця.
Отже, знаходимо компоненти вектора X*:
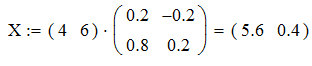
| (3.14) |
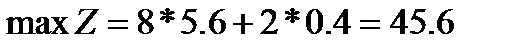
| (3.15) |
Настуним кроком перевіримо правильність розв’язання задачі за допомогою MathCad. Обов’язково треба зауважити, що через округлення можливі незначні незбіжності у значеннях цільових функцій. Розв’яжемо перш за все пряму задачу (рис. 3.1).
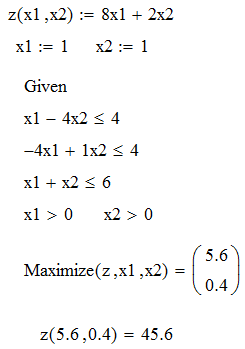
Рисунок 3.1 – Розв’язання прямої задачі
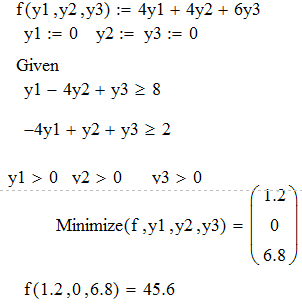
Рисунок 3.2 – Розв’язання двоїстої задачі
ЗАВДАННЯ 4
Однорідний вантаж, зосереджений у m постачальників в обсягах  (
(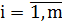 ), необхідно поставити n споживачам в обсягах
), необхідно поставити n споживачам в обсягах  (
(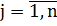 ).
).
Відомі 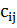 (
(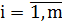 ;
;  ) – вартості перевезення одиниці вантажу від кожного i-го постачальника до кожного j-го споживача.
) – вартості перевезення одиниці вантажу від кожного i-го постачальника до кожного j-го споживача.
Необхідно скласти такий план перевезень, використовуючи метод stepping-stone, при якому запаси усіх постачальників вивозяться повністю й сумарні витрати на перевезення усього вантажу мінімальні. Вхідні дані транспортної задачі наведені у таблиці 4.1.
Таблиця 4.1 – Вхідні дані задачі
| Постачальник | Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача | Запаси | |||
| Замовник | |||||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потреба |
Розв’язання завдання.
Транспортна задача – це специфічна задача лінійного програмування, що застосовується для визначення найекономічнішого плану перевезення однорідної продукції від постачальників до споживачів.
Перш за все побудуємо математичну модель задачі. Нехай xij – кількість продукції, що перевозиться від і-го постачальника до j-го замовника 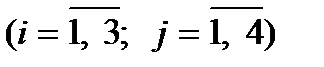 . Загальні витрати на транспортування визначаються як сума добутків обсягів перевезеної продукції на вартість транспортування одиниці продукції до відповідного замовника. Витрати мають бути мінімальними.
. Загальні витрати на транспортування визначаються як сума добутків обсягів перевезеної продукції на вартість транспортування одиниці продукції до відповідного замовника. Витрати мають бути мінімальними.
За умовою, дана транспортна задача є незбалансованою. Щоб збалансувати дану задачу, необхідно ввести фіктивного споживача, перевезення до якого дорівнюють 0. Збалансована транспортна задача наведена в таблиці 4.2.
Таблиця 4.2 – Збалансована транспортна задача
| Постачальник | Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача | Запаси | |||
| Замовник | |||||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| A4 | |||||
| Потреба |
Для розв’язання даної задачі скористаємося методом потенціалів. Для початку побудуємо базове рішення задачі, використовуючи метод северно-західного кута.
Рішення задачі представлене в таблиці 4.3.
Таблиця 4.3 – Перший опорний план, побудований за методом северно-західного кута
| Постачальник | Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача | Запаси | |||
| Замовник | |||||
| В1 | В2 | В3 | В4 | ||
| А1 | 1[30] | 2[10] | |||
| А2 | 1[15] | 3[15] | |||
| А3 | 5[3] | 1[17] | |||
| A4 | 0[3] | ||||
| Потреба |
Реалізація першого опорного плану призведе до наступних загальних витрат:
| Z = 1*30+2*10+1*15+3*15+5*3+1*17+0*3=142 | (4.1) |
Одержано опорний план, який є допустимим, оскільки всі вантажі з баз вивезені, потреба магазинів задоволена, а план відповідає системі обмежень транспортної задачі.
Число зайнятих клітин таблиці, їх 7, m + n - 1 = 7. Отже, опорний план є невиродженим.
Перевіримо оптимальність опорного плану. Знайдемо попередні потенціали ui, vi. по зайнятих клітинам таблиці, в яких ui + vi = cij, вважаючи, що u1 = 0.
Таблиця 4.4 – Попередні потенціали ui, vi
| v1=1 | v2=2 | v3=4 | v4=0 | |
| u1=0 | 1[30] | 2[10] | ||
| u2=-1 | 1[15] | 3[15] | ||
| u3=1 | 5[3] | 1[17] | ||
| u4=0 | 0[3] |
Опорний план не є оптимальним, тому що існують оцінки вільних клітин,для яких ui +vi> cijВибираємо максимальну оцінку вільної клітини (4,3): 0Для цього в перспективну клітку (4, 3) поставимо знак «+», а в інших вершинахбагатокутника чергуються знаки «-», «+», «-».
Таблиця 4.5 – Оцінка плану
| Постачальник | Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача | Запаси | |||
| Замовник | |||||
| В1 | В2 | В3 | В4 | ||
| А1 | 1[30] | 2[10] | |||
| А2 | 1[15] | 3[15] | |||
| А3 | 5[3][-] | 1[17][+] | |||
| A4 | 0[+] | 0[3][-] | |||
| Потреба |
З вантажів хij стоять в мінусових клітинах, вибираємо найменше, тобто у = min (4, 4) = 3. Додаємо 3 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 3 з Хij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план.
Таблиця 4.6 – Другий опорний план
| Постачальник | Вартості перевезень одиниці вантажу від кожного i-го постачальника до кожного j-го споживача | Запаси | |||
| Замовник | |||||
| В1 | В2 | В3 | В4 | ||
| А1 | 1[30] | 2[10] | |||
| А2 | 1[15] | 3[15] | |||
| А3 | 5[0] | 1[20] | |||
| A4 | 0[3] | ||||
| Потреба |
Таблиця 4.7 – Попередні потенціали ui, vi
| v1=1 | v2=2 | v3=4 | v4=0 | |
| u1=0 | 1[30] | 2[10] | ||
| u2=-1 | 1[15] | 3[15] | ||
| u3=1 | 5[0] | 1[20] | ||
| u4=-4 | 0[3] |
Опорний план є оптимальним, оскільки всі оцінки вільних клітин задовольняють умові ui + vi <= cij.
Реалізація першого опорного плану призведе до наступних загальних витрат:
| Z = 1*30+2*10+1*15+3*15+5*0+1*20+0*3=130 | (4.3) |
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается, как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. Транспортная задача является по теории сложности вычислений NP-сложной и входит в класс сложности NP. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
Перевіримо правильність виконання завдання за допомогою MathCad (рис. 4.3).

Рисунок 4.3 – Результат вирішення транспортної задачі
ЗАВДАННЯ 5
Визначити точку та характер умовного екстремуму функції за методом множників Лагранжа.
 ,
,
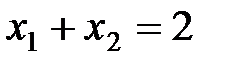
Розв’язання завдання.
Одним із методів розв’язання задач нелінійного програмування є метод множників Лагранжа [4].
Цей метод використовється для розв’язання задач виду:
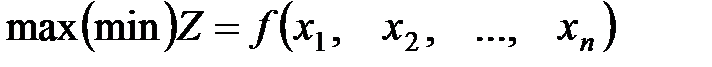
| (5.1) |
за умов:
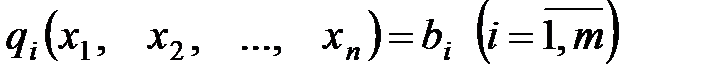
| (5.2) |
де функції 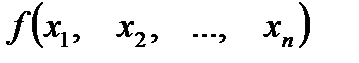 і
і 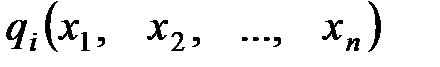 диференційовані.
диференційовані.
Ідея цього методу полягає у заміні поставленої задачі на простішу: на знаходження екстремуму складнішої функції, але без обмежень. Ця функція має назву функції Лагранжа. Вона має наступний вигляд:
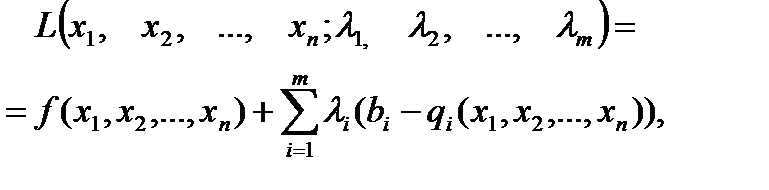 (5.3) (5.3)
|
де 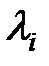 – деякі невідомі величини, що називаються множниками Лагранжа.
– деякі невідомі величини, що називаються множниками Лагранжа.
Запишемо функцію Лагранжа для поставленої задачі. Вона матиме наступний вигляд:
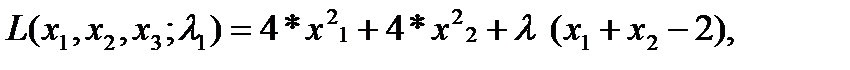
| (5.4) |
Наступним кроком знаходимо частинні похідні за всіма змінними функції L, а потім прирівнюємо їх до нуля. Отримаємо наступну систему:
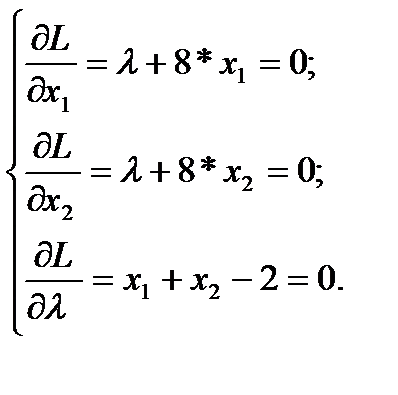 (5.5) (5.5)
|
Розв’язавши дану систему отримаємо стаціонарні точки  та
та 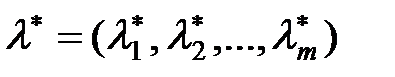 – стаціонарні точки. Для даної системи
– стаціонарні точки. Для даної системи  та
та 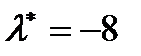 .
.
Щоб визначити характер умовного екстремуму, за функцією Лагранжа будуємо матрицю Гессе розмірністю  . Ця матриця має блочний характер:
. Ця матриця має блочний характер:
 (5.6) (5.6)
|
де О – матриця розмірністю (m×m), що складається з нульових елементів,
Р – матриця розмірністю (m×n), елементи якої визначаються наступним чином:
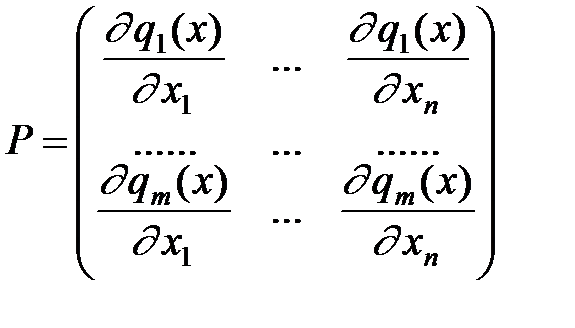 (5.7)
(5.7)
Р′ – транспонована матриця до Р розмірністю (n×m),
Q – матриця розмірністю (n× n) виду:
 ,
,  (5.8)
(5.8)
Для поставленої задачі матриця Гессе матиме вигляд:
| (5.9) |
Розрахувавши мінори даної матриці (Δ4 = 64, Δ5 = 8), отримаємо незнакозмінний числовий ряд, що означає, що Х* – точка мінимуму.
Далі обчислимо значення цільової функції у цій точці.

| (5.10) |
Отже, використавши метод множників Лагранжа, з’ясовано, що Х*=( ) – точка мінимуму.
) – точка мінимуму.
Для того, щоб перевірити правильність виконання даного завдання, скористаємося програмним забезпеченням MathCad (рис. 5.1).

Рисунок 5.1 – Вирішення завдання у MathCad
ЗАВДАННЯ 6
Розв’язати задачу опуклого програмування.
Z=x21+x22-6x1-4x2 (min);
x1 + 2x2 ≤ 12;
2x1 + x2 ≤ 6;
x1 ≥ 0, x2 ≥ 0, x3≥ 0
Розв’язання завдання.
Розв’яжемо дану задачу за допомогою методу множників Лагранжа, а потім застосуємо теорему Куна-Таккера. Метод множників Лагранжа був описаний у попередньому завданні, тому перейдемо безпосередньо до розрахунків.
Запишемо функцію Лагранжа для поставленої задачі. Вона матиме наступний вигляд:
 (6.1)
Наступним кроком знаходимо частинні похідні за всіма змінними функції L, а потім прирівнюємо їх до нуля. Отримаємо наступну систему: (6.1)
Наступним кроком знаходимо частинні похідні за всіма змінними функції L, а потім прирівнюємо їх до нуля. Отримаємо наступну систему:

|
Розв’язавши дану систему отримаємо стаціонарні точки  та
та 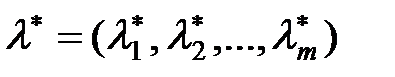 – стаціонарні точки. Для даної системи
– стаціонарні точки. Для даної системи 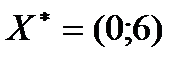 та
та 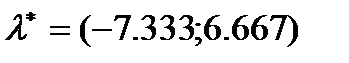 .
.
Значення функції в цій точці наведені на рисунку 6.1
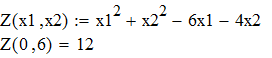
Рисунок 6.1 – Значення функції в точці екстремуму
Застосуємо теорему Куна-Таккера.
Якщо задано є задача нелінійного програмування, де функції 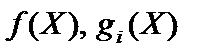
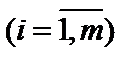 диференційовні і вгнуті по Х, то для того, щоб вектор
диференційовні і вгнуті по Х, то для того, щоб вектор 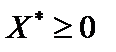 був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор
був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор 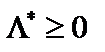 , що пара (
, що пара (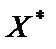 ,
,  ) була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови,зображені на рис 6.2:
) була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови,зображені на рис 6.2:
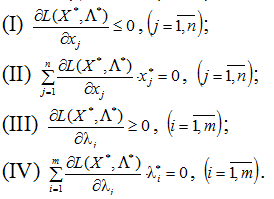
Рисунок 6.2 – Умови що вказують на те, що знайдена точка – сідлова
Тепер підставимо значення Х* у наведені вище умови. Отримаємо:
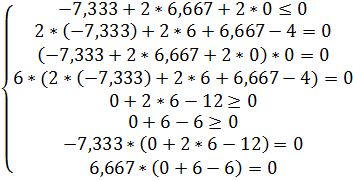
З наведеного вище рівняння бачимо, що точка Х* задовольняє всім умовам теореми Куна – Таккера, а отже є сідловою точкою функції Лагранжа і рішенням задачі опуклого програмування.

Рисунок 6.3 – Вирішення завдання у MathCad
ЗАВДАННЯ 7
Створити інформаційну базу у вигляді матриці котирувань продажу (С) n видів акцій  у періоди часу t, t =0,...,T (вказати джерело інформації):
у періоди часу t, t =0,...,T (вказати джерело інформації):

де Сi,t (i =1,...,n; t = 0,...,T) – ціна і-тої акції у періоді часу t, n>=5, T>=10.
Здійснити порівняльний аналіз ризикованості інвестування у цінні папери на основі даних про котирування цінних паперів з матриці С.
Аналіз здійснити на основі показників:
- середньоквадратичного відхилення (σ) норми прибутку цінного паперу;
- семіквадратичного відхилення (SSV) норми прибутку цінного паперу;
- коефіцієнта варіації (CV) для кожного виду цінного паперу;
- коефіцієнта семіваріації (SV) для кожного виду цінного паперу.
Проаналізувати привабливість цінних паперів на основі розрахованих показників.
Розв’язання завдання.
Оцінювання ризику – необхідний атрибут у стратегії і тактиці ефективного менеджменту. Тому важливою є розробка методик кількісної оцінки ступеня ризику, удосконалення механізму моніторингу, контролювання економічного ризику та керування ним на засадах системного аналізу.
Зробимо порівняльний аналіз ризикованості інвестування в цінні папери на основі даних про котирування акцій українських підприємств впродовж 2010 - 2011 років. Дані взяті з електронного ресурсу, розміщеного за адресою: www.i-nvest.net (таблиця 7.1).
Таблиця 7.1 – Котирування акцій українських підприємств впродовж 2010-2011 рр.
| Емітент | Періоди | ||||||||||
| ОАО «Киевградосервис» | 12,8 | 13,2 | 13,3 | 13,1 | 13,7 | 13,8 | 14,0 | 14,1 | 14,1 | 14,6 | 12,8 |
| ОАО «Берест» | 21,6 | 21,9 | 21,9 | 21,8 | 21,8 | 21,5 | 21,3 | 22,0 | 22,0 | 21,7 | 21,6 |
| ОАО «Гранд-Інвест IК» | 28,6 | 28,8 | 28,9 | 30,1 | 30,2 | 30,2 | 30,1 | 28,8 | 28,5 | 28,6 | 28,6 |
| ОАО«Градострой» | 7,8 | 7,4 | 7,6 | 7,3 | 7,3 | 7,0 | 6,9 | 6,8 | 6,5 | 6,4 | 7,8 |
| ОАО«Гранит» | 42,4 | 42,6 | 42,6 | 42,8 | 43,7 | 44,0 | 43,5 | 44,0 | 44,0 | 44,2 | 42,4 |
| ОАО«ДБК-1» | 12,4 | 12,3 | 12,8 | 13,0 | 13,1 | 13,1 | 13,3 | 13,7 | 13,9 | 13,6 | 12,4 |
Основною характеристикою акції є норма прибутку. Норма прибутку цінних паперів залежить від трьох факторів: ціни покупки, проміжних виплат (дивідендів) та ціни продажу [1].
Тоді, норма прибутку звичайної акції у період часу t визначається за формулою:
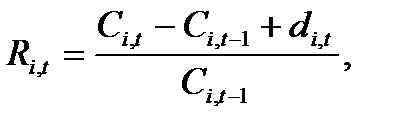 (7.1) (7.1)
|
де Ri,t – норма прибутку і-ї акції;
Ci,t – ціна і-ї акції у період часу t;
di,t – дивіденди, що виплачуються у період часу t по і-й акції.
На основі наведеної вище формули створимо таблицю норми прибутку (табл. 7.2).
Таблиця 7.2 – Норма прибутку по кожному виду акцій
| R1 | 0,02 | 0,03 | 0,00 | -0,01 | 0,04 | 0,01 | 0,02 | 0,01 | 0,00 | 0,03 |
| R2 | 0,01 | 0,01 | 0,00 | 0,00 | 0,00 | -0,01 | -0,01 | 0,03 | 0,00 | -0,01 |
| R3 | 0,00 | 0,00 | 0,00 | 0,04 | 0,00 | 0,00 | 0,00 | -0,04 | -0,01 | 0,01 |
| R4 | 0,02 | -0,06 | 0,03 | -0,03 | -0,01 | -0,04 | -0,02 | 0,00 | -0,05 | -0,02 |
| R5 | 0,00 | 0,01 | 0,00 | 0,00 | 0,02 | 0,01 | -0,01 | 0,01 | 0,00 | 0,01 |
| R6 | 0,00 | -0,01 | 0,04 | 0,02 | 0,01 | 0,00 | 0,01 | 0,03 | 0,01 | -0,02 |
Приймаємо гіпотезу, що норми прибутку акцій є випадковими величинами. Тоді на основі таблиці 7.2 ми можемо обчислити статистичну оцінку сподіваної норми прибутку для кожного виду акцій. Його можна розглядати як результат, котрий ми очікуємо отримати в середньому. Оцінку сподіваної норми прибутку будемо розраховувати за формулою:
 (7.2) (7.2)
|
Після проведення розрахунків отримаємо: m1 = 0,0154; m2 = 0,0012; m3 = 0,0002; m4 = -0.0173; m5 = 0,0046; m6.=0,0101
Для оцінювання степеню ризику використаємо варіацію (дисперсію) можливих результатів навколо сподіваного прибутку та середньоквадратичне відхилення.
Статистична оцінка дисперсії норми прибутку обчислюється за формулою:

| (7.3) |
Формула для обчислення статистичної оцінки середньоквадратичного відхилення норми прибутку має вигляд:
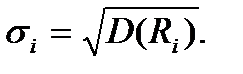
| (7.4) |
Маємо наступні оцінки міри розсіювання можливих результатів навколо сподіваного прибутку: D(R1) = 0,00025; D(R2) = 0,00017; D(R3) = 0,00044; D(R4) = 0,00073; D(R5) = 0,0006; D(R6) = 0.00031.
Значення середньоквадратичного відхилення мають наступний вигляд: s1 = 0.016; s2 = 0,013; s3 = 0,021; s4 = 0,027; s5 = 0,008; s6 =0,018.
Отже, вкладання грошей в акції ОАО «Гранит» є менш ризикованим, що підтверджують як значення дисперсії, так і значення середньоквадратичного відхилення.
Якщо випадкова величина Х відображає прибутки, і має місце від’ємне відхилення, то це є ознакою несприятливої ситуації. В той же час додатне відхилення вказує на те, що реалізація випадкової величини (прибутку) є більшою, ніж сподівана величина, і це для інвестора є, очевидно, кращою тобто сприятливою ситуацією.
Реалізацією саме цього підходу є такі оцінки як семіваріація і семіквадратичне відхилення.
Для розрахунку значення семіваріації скористаємось формулою:
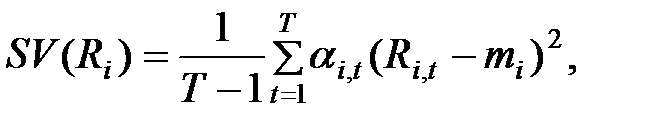
| (7.5) |
де αi,t – індикатор несприятливих відхилень, який розарховується за наступною формулою:
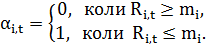
| (7.6) |
Маємо наступні значення семіваріації: SV(R1) = 0,0001; SV(R2) = 0,0001; SV(R3) = 0,0002; SV(R4) = 0,0003; SV(R5) = 0,00003; SV(R6) = 0,0001.
З практичного погляду зручніше застосовувати так зване семіквадратичне відхилення, яке можна подати за формулою:

| (7.7) |
Провівши розрахунки за приведеною вище формулою, отримаємо SSV(R1) = 0,011; SSV(R2) = 0,007; SSV(R3) = 0,015; SSV(R4) = 0,018; SSV(R5) = 0,005; SSV(R6) = 0,012.
Отже, можна сказати, що чим більшою буде величина SV(Rі) чи SSV(Rі), тим більшим буде ступінь ризику.
Коли сподівані доходи проектів суттєво різняться між собою, то для порівняння їх ризикованості неадекватно використовувати оцінки ступеня ризику, задані в абсолютному вираженні. У цьому разі можна скористатися такими показниками ризикованості, як коефіцієнт варіації (CV) та коефіцієнт семіваріації (CSV), які обчислюються відповідно за формулами (7.8) та (7.9):
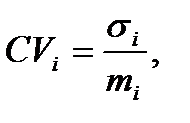 (7.8) (7.8)
| |
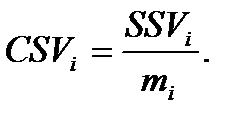 (7.9) (7.9)
|
Значення коефіцієнта варіації для даних завдання матиме наступний вигляд: CV1 = 1,033; CV2 = 10,715; CV3 = 134,56; CV4 = -1,055; CV5 =1,141; CV6 = 1,182.
Коефіцієнт семіваріації набуває значень: CSV1 = 0,709; CSV2 = 5,891; CSV3 = 99,087; CSV4 = -1,055; CSV5 = 1,141; CSV6 = 1,182
Цим коефіцієнтам можна надати таке економічне трактування: коефіцієнт варіації - це величина ризику відхилень, що припадають на одиницю сподіваного доходу, а коефіцієнт семіваріації - величину ризику несприятливих відхилень, що припадають на одиницю сподіваного доходу. А тому можна дійти висновку, що ці коефіцієнти мають від’ємний інгредієнт (чим менші їх значення для проекту, тим меншим ризиком у відносному вираженні він обтяжений).
Слід зауважити, що дані коефіцієнти можуть використовуватися лише за умови, що економічний показник Х, з позиції якого аналізуються проекти, має додатний інгредієнт і при цьому його сподіване значення більше нуля.
Отже, на основі розрахованих показників можна стверджувати, що найбільш привабливими є акції ОАО «Гранит» та ОАО «Градострой».
ЗАВДАННЯ 8
На основі матриці С отримати матрицю норм прибутку цінних паперів R, обчислити сподівані норми прибутку mi, дисперсії норм прибутку цінних паперів Di, середньоквадратичні відхилення та сформувати матрицю Δ відхилень значень норми прибутку Ri,t від сподіваної норми прибутку mi для усіх цінних паперів.
На основі показників сподіваної норми прибутку акцій, дисперсії норми прибутку акцій (як показника кількісної оцінки ризику) та ступеня кореляції між нормами прибутку акцій обрати оптимальний портфель цінних паперів з позицій:
- мінімального ризику;
- мінімального ризику при заданій величині норми прибутку портфеля;
- максимальної норми прибутку за обмеження на ризик портфеля.
Розв’язання завдання.
Портфель цінних паперів – це розподіл коштів у певного інвестора між різними активами (акції, облігації) в найбільш вигідній та безпечній пропорції. Такий розподіл інвестицій за різними “адресами” знижує ризик, забезпечує більшу стійкість доходів (прибутків) за будь-яких коливань дивідендів і ринкових цін на цінні папери.
Базовими положеннями у теорії цінних паперів є те, що норма прибутку (дохідність) інвестицій у цінні папери – це випадкова величина; інвестор оцінює альтернативні рішення за двома параметрами – сподівана норма прибутку як показник ефективності інвестицій та середньоквадратичне відхилення норми прибутку як показник ступеня ризику; інвестор прагне збільшення ефективності та зменшення ступеня ризику [2].
Для оцінки оптимального портфелю цінних паперів використаємо показники сподіваної норми прибутку, розрахованої у завданні 7 (табл. 8.1).
Таблиця 8.1 – Показники сподіваної норми прибутку акцій
| R1 | 0,10 | -0,15 | 0,10 | -0,04 | -0,02 | -0,04 | 0,10 | 0,05 | 0,19 | 0,00 |
| R2 | 0,18 | -0,03 | -0,07 | 0,03 | -0,04 | 0,02 | 0,14 | 0,02 | 0,09 | -0,08 |
| R3 | 0,01 | -0,15 | 0,05 | 0,01 | -0,12 | -0,09 | 0,13 | 0,08 | 0,12 | -0,01 |
| R4 | 0,02 | 0,05 | -0,04 | 0,08 | -0,05 | -0,05 | -0,07 | 0,00 | 0,18 | 0,29 |
| R5 | 0,41 | 0,01 | 0,02 | 0,00 | 0,01 | -0,01 | -0,14 | 0,00 | -0,02 | -0,06 |
| R6 | 0,12 | -0,09 | 0,00 | 0,05 | -0,16 | -0,02 | 0,14 | 0,07 | 0,03 | 0,03 |
Відмітимо, що норма прибутку - це один із основних критеріїв, яким керуються інвестори у процесі прийняття рішення щодо інвестування в цінні папери. Згідно з гіпотезою, що норма прибутку є випадковою величиною. Ці ймовірності залежать від ситуації на ринку цінних паперів, яка залежить, у свою чергу, від багатьох чинників, зокрема, від загальної економічної ситуації.
Позначимо через xi частку і-го цінного паперу у портфелі. Для значень xi виконуються наступні умови:
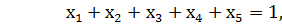
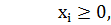 
| (8.1) |
Тоді, сподівана норма прибутку портфеля обчислюється за формулою:
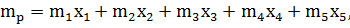
| (8.2) |
де 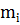 - сподівана норма прибутку відповідного цінного паперу.
- сподівана норма прибутку відповідного цінного паперу.
Дисперсія портфеля цінних паперів обчислюється за формулою (8.3).

| (8.3) |
де 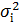 - дисперсія і-го цінного паперу;
- дисперсія і-го цінного паперу;
cov (Ri; Rj) – коваріація між i-тим та j-тим цінними паперами.
Отже, перш за все необхідно розрахувати значення коваріації між нормами прибутку акцій. Побудуємо коваріаційну матрицю, використовуючи для цього матрицю Δ – матрицю відхилень норми прибутку від сподіваної норми прибутку. Отже, коваріаційна матриця розраховується за формулою:
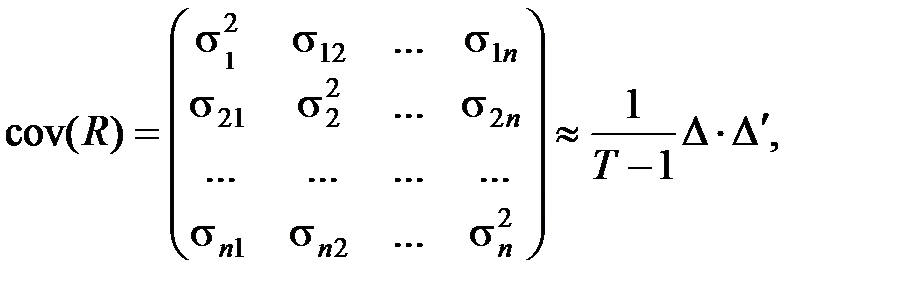 (8.4) (8.4)
|
де  - матриця, транспонована до матриці Δ.
- матриця, транспонована до матриці Δ.
Введемо позначення:
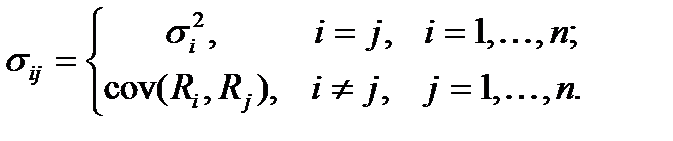 (8.5)
(8.5)
Отже, формула дисперсії матиме наступний вигляд:
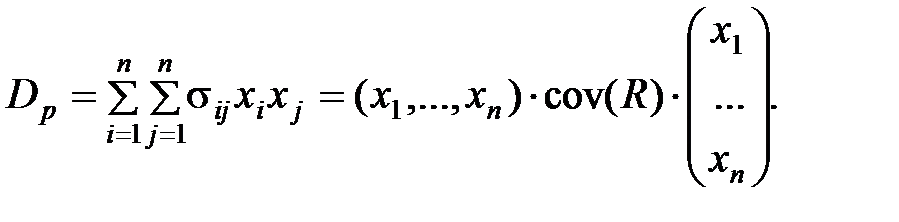 (8.6) (8.6)
|
Для даного завдання матриця Δ має наступний вигляд (рис. 8.1):

Рисунок 8.1 – Матриця відхилень норми прибутку від сподіваної норми прибутку
За формулою (8.4) коваріаційна матриця матиме наступний вигляд (рис.8.2):

Рисунок 8.2 – Коваріаційна матриця
Отже, перше завдання полягає в тому, щоб побудувати портфель цінних паперів з мінімальним ризиком. Для цього необхідно, щоб виконувались наступні умови:
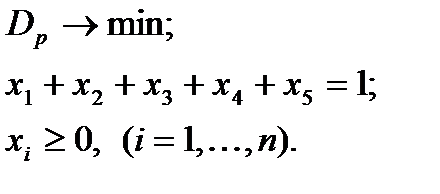 (8.7) (8.7)
|
Через складність аналітичних розрахунків перейдемо відразу до результатів поставленого завдання (рис. 8.3 – 8.4).

Рисунок 8.3 – Побудова портфеля цінних паперів із мінімальним ризиком

Рисунок 8.4 – Задання умов для побудови портфеля цінних паперів із мінімальним ризиком
Отже, бачимо, що оптимальний портфель цінних паперів із мінімальним ризиком складається із цінних паперів п’яти видів і не включає в себе акції ОАО «Градострой».
Портфель цінних паперів міститиме в собі 20% акцій ОАО «Киевградосервис», 24% акцій ОАО «Берест» 20% акцій ОАО «Гранд-Інвест IК», 17% акцій ОАО «Гранит» і 16% акцій ОАО «ДБК-1»
Наступним кроком побудуємо портфель цінних паперів із заданою сподіваною нормою прибутку та мінімальним ризиком.
Для цього треба знати таку структуру портфеля, щоб виконувались наступні умови:
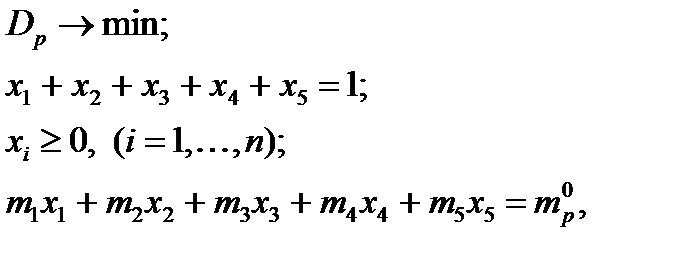 (8.8) (8.8)
|
де  – задане суб’єктивно значення сподіваної норми прибутку портфеля, яку бажає отримати інвестор.
– задане суб’єктивно значення сподіваної норми прибутку портфеля, яку бажає отримати інвестор.
Значення  повинно задовольняти умову:
повинно задовольняти умову:
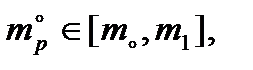
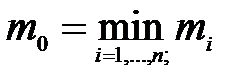 ;
; 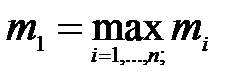 . (8.9)
. (8.9)
У даному випадку задамо значення сподіваної норми прибутку портфеля як 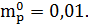
Перейдемо до результатів завдання (рис. 8.5 – 8.6).
У даному випадку портфель цінних паперів складається із п’ятьох видів акцій. Портфель цінних паперів міститиме в собі 40% акцій ОАО «Киевградосервис», 6% акцій ОАО «Берест» 15% акцій ОАО «Гранд-Інвест IК», 2% акцій ОАО «Гранит» і 34% акцій ОАО «ДБК-1»

Рисунок 8.5 – Побудова портфеля цінних паперів із мінімальним ризиком та заданою сподіваною нормою прибутку

Рисунок 8.6 – Завдання умов для побудови портфеля із мінімальним ризиком та заданою сподіваною нормою прибутку
Дата добавления: 0000-00-00; просмотров: 249 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Эльмир Кулиев | | | Опорний стрибок |