Задания для самостоятельного решения.

Упражнение 2.1. Найти длины сторон и координаты точек, лежащих на серединах сторон, для треугольника с вершинами: a ) A(2;0), B(4;3), C(3;6);
b ) A(2;-1), B(4;3), C(-2;1); c ) A(-2;4), B(5;-1), C(2;3).

Упражнение 2.2. Написать уравнение прямой, проходящей через заданные точки A и B, выписать ее угловой коэффициент и координаты вектора нормали: а) A(-1;3), B(4;-2); b) A(3;2), B(2;-1); c) A(1;-3), B(-1;5);
d) A(1;3), B(4;-3); e) A(2;3), B(2;-2); f) A(4;5), B(-3;5).

Упражнение 2.3. Найти координаты вершин иравнения и длины медиан в треугольнике, стороны которого заданы уравнениями: а) , , ; b) , , .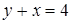

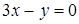Упражнение 2.4. Найти координаты точки пересечения медиан в треугольнике с вершинами A(-4;2), B(2;-5), C(5;0).

Упражнение 2.5. Написать уравнение прямой, проходящей через заданную точку A и образующей с положительным направлением оси OX угол :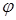

а) A(2;3), 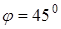; b ) A(0;0), 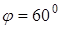; c) A(1;3), ;
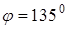d) A(5;-6), 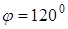; e) A(4;5), .

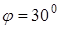Упражнение 2.6. Определить угол между прямыми:

А),; b),; c),.

Упражнение 2.7. Среди данных прямых найти параллельные и перпендикулярные:

a) , , ,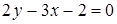

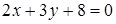
b) , , ,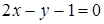

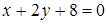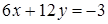с) , , ,

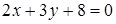
d) , , ,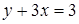

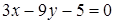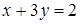Упражнение 2.8. Написать уравнения прямых, проходящих через заданную точку параллельно и перпендикулярно заданной прямой:

а) A(2;3), 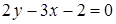; b) A(3;-6), 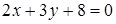; c) A(-2;0), .

Упражнение 2.9. Написать уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой, найти точку пересечения прямых: а) A(-3;2), 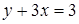; b) A(1;-5), ; c) A(0;-3), .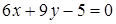

Упражнение 2.10. Написать параметрическое уравнение прямой, проходящей через указанную точку параллельно заданному вектору, привести уравнение к общему виду: а) A(2;3), 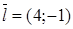; b) A(-1;5), ;
c) A(-2;3), .

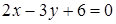Упражнение 2.11. Привести общие уравнения прямых к уравнениям в отрезках, построить прямые: a) ; b) ; c) .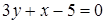

Упражнение 2.12. Составить уравнения прямых, проходящих через точку A(-4;6) и отсекающих от осей координат треугольник площадью 6 см².

Упражнение 2.13. Найти координаты вершин треугольника, образованного прямыми , , 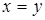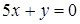. Построить треугольник, найти тангенсы его углов и координаты точки пересечения высот.

Упражнение 2.14. Найти координаты вершин треугольника, образованного прямыми 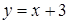, , 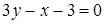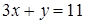. Построить этот треугольник, найти его площадь.

Упражнение 2.15. В треугольнике с заданными вершинами найти уравнения сторон и высот, длины медиан и средних линий: а) A(5;3), B(2;3), C(0;-3) b) A(-3;7), B(7;1), C(-1;-1).

Упражнение 2.16. Записать канонические и параметрические уравнения прямой, проходящей через заданную точкупараллельно заданному вектору; привести к общему виду: a) A(4;3;2), 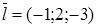; b) A(-2;-3;1), .

Упражнение 2.17. Записать канонические и параметрические уравнения прямой, проходящей через заданные точки, привести к общему виду:

a) A(-1;2;3), B(2;6;-2); b) A(3;-1;4) и B(1;3;2).

Упражнение 2.18. Решить графически систему линейных неравенств:

1)	2)	3)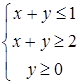
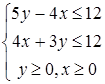
4)	5)	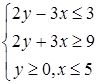6)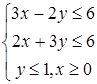
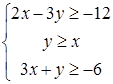
7)	8)	9)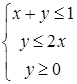

Дата добавления: 2015-10-30