Оценочные средства для текущего контроля успеваемости и промежуточной аттестации

Текущая аттестация проводится еженедельно. Критерии формирования оценки – посещаемость занятий, активность студентов на семинарских занятиях, уровень подготовки к семинарским занятиям, выполнение домашних заданий.

Примеры домашних задач содержатся в разделах «Задачи для самостоятельного решения» в учебном пособии Волков В.Т., Ягола А.Г. «Интегральные уравнения. Вариационное исчисление (методы решения задач).» М.: КДУ, 2009., доступном по адресу http://yagola.professorjournal.ru/integral_equation

Промежуточная аттестация проводится в середине (по 1 части курса - интегральным уравнениям) и в конце семестра (по второй части курса – вариационному исчислению) в форме контрольных работ с оценкой. Критерии формирования оценки – уровень знаний пройденной части курса.

Примерные варианты контрольных работ:

Контрольная работа №1 (интегральные уравнения)

1. Найти характеристические числа и собственные функции .

2. Исследовать разрешимость при различных значениях 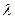и решить интегральное уравнение Фредгольма 2-го рода .

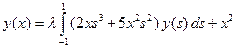3. Решить уравнение Фредгольма 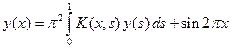с симметрическим непрерывным ядром , .

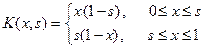4. Построить резольвенту уравнения Фредгольма .

5. Проверить, что 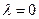не является собственным значением оператора с указанными граничными условиями, и свести задачу Штурма-Лиувилля к интегральному уравнению Фредгольма с симметрическим ядром: .

6. Найти собственные значения и собственные функции задачи Штурма-Лиувилля:

а) , ;

б) , ;

в) , .

Контрольная работа №2 (вариационное исчисление)

1. Исследовать на экстремум функционал 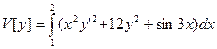в задаче с закрепленными концами , .

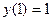Достаточные условия проверить с помощью функции Вейерштрасса.

2. Исследовать на экстремум функционал 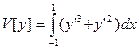в задаче с закрепленными концами , .

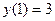Достаточные условия проверить в форме Лежандра.

3. Найти минимальное расстояние от прямой 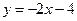до параболы .

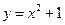4. Исследовать на экстремум функционал с условиями , , , 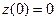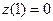и голономной связью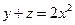

5. Исследовать на экстремум функционал 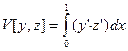с условиями , , , , , .

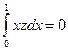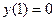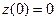Итоговая аттестация - экзамен.

Экзамен по курсу "Интегральные уравнения. Вариационное исчисление" состоит из 2-х частей.

1-я часть экзамена – письменная работа на знание определений, формулировок теорем и имение решать простые задачи.

2-я часть экзамена - теоретическая. К ней допускаются только студенты, успешно выполнившие первую. Для получения оценки "хорошо" и "отлично" необходимо уметь доказывать утверждения и теоремы, включенные в изучаемый курс.

Полный перечень вопросов и задач к первой и второй части экзамена доступен по адресу: http://yagola.professorjournal.ru/integral_equation

Образец билета первой части экзамена

1. Записать интегральное уравнение Фредгольма 2-го рода.

2. Найти норму функции в пространстве .

3. Найти характеристические числа и собственные функции .

4. Сформулировать определение сжимающего оператора.

5. Сформулировать теорему о необходимом условии экстремума функционала в задаче с закрепленными концами .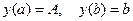

6. Сформулировать постановку задачи поиска экстремума функционала , считая, что левый конец закреплен, а правый - подвижен.

Образец билета второй части экзамена:

1. Описать процесс построения собственных значений и собственных функций вполне непрерывного самосопряженного оператора , действующего в бесконечномерном евклидовом пространстве.

2. Доказать, что любое интегральное уравнение Фредгольма 2 рода с невырожденным ядром при фиксированном 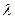можно заменить эквивалентным интегральным уравнением с вырожденным ядром.

3. Доказать, что необходимым условием экстремума функционала является равенство нулю его вариации при условии, что вариация существует.

Дата добавления: 2015-10-30