Залежні і незалежні ВВ. Умовні закони розподілу.

ВВ називаються незалежними, якщо закон розподілу кожної з них не залежить від того, які можливі значення приймають інші ВВ. В противному випадку вони називаються залежними.

Умовним законом розподілу ВВ Х називається закон її розподілу, за умови, що У прийме значення у. Нехай (Х;У) – НВВ. У випадку залежності Х і У їх умовні закони розподілу:

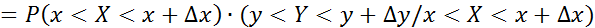
Якщо останню рівність розділити на Δx∙Δy і перейти до границі Δx->0; Δy->0, то отримаємо: f(x;y)=f₁(x)∙f(y/x)

Аналогічно можна отримати:

f(x;y)=f₂(y)∙f(x/y), де f(x;y) - густина розподілу сист. ВВ x;y

(X;Y): f₁(x) – X; f₂(y) – Y

Звідки:

Відповідно:

Теорема. Якщо система ВВ складається з незалежних ВВ, то густина розподілу цієї системи дорівнює добутку густини розподілу складових. Тобто f(x;y)=f₁(x)∙f₂(x)

Оскільки, якщо Х і У – незалежні, то f(x/y)=f₁(x); f(y/x)=f₂(x)

Нехай Х і У – залежні ВВ. Якщо вони дискретні, то умовне математичне сподівання:

Якщо ж Х і У – залежні, тоді дисперсія:

Якщо ж Х і У – неперервні, тоді дисперсія:

Початкові і центральні моменти ВВ

Нехай маємо систему ВВ (Х;У). Початковим моментом порядку K+S цієї системи називається величина, що визначається формулою:

μ_k,s=M[X^k∙Y^S]

Якщо Х і У – дискретні, тоді

Якщо Х і У – неперервні, тоді

Центральним моментом порядку K+S цієї системи ВВ називається величина, визначена формулою:

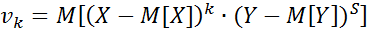
Якщо Х і У – дискретні, тоді центральний момент буде визначатись формулою:

Якщо Х і У – неперервні, тоді

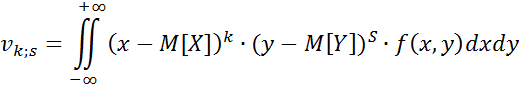
Очевидно, що початковий момент порядку 1+0:

μ_1,0 = M[X]; μ_0,1 = M[Y]

Центральний момент порядку 2+0:

v_2;0 = M[(X - M[X])²] = D[X]

v_0;2 = D[Y]

Кореляційний момент. Коефіцієнт кореляції.

Кореляційним моментом називається центральний момент системи (Х;У) порядку 1+1:

V_1;1 = M[(X - M[X]) ∙ (Y - M[Y])] = K_x,y і визначає залежність ВВ Х і У.

Властивості кореляційного моменту:

1) K_x,y = K_y,x

2) K_xx = M[(X - M[X])²] = D[X]

3) |K_xy| ≤

Означення.

Якщо ВВ Х та У – незалежні, то їх кореляційний момент дорівнює нулю і називаються такі ВВ некорельовані.

Коефіцієнт кореляції визначається формулою:

Властивості коефіцієнту кореляції:

1) r_xy = r_yx

2) r_xx = 1

3) |r_xy| ≤ 1

Дата добавления: 2015-10-23