Початкові і центральні моменти ВВ

Математичне сподівання ВВ

Нехай дана дискретна ВВ – Х.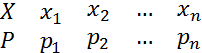

Математичне сподівання ДВВ називається M[X] =

Якщо Х – НВВ f(x), тоді

Властивості математичного сподівання:

1) Якщо С – стала (невипадкова) величина, то математичне сподівання такої величини дорівнює самій цій величині, тобто M[C]=C

2) M[C∙X] = C ∙ M[X]

3) Математичне сподівання суми двох випадкових величин: M[X+Y] = M[X] + M[Y].

Доведення

Нехай дане M[X+Y], де Х – ДВВ з вказаним вище законом розподілу.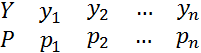

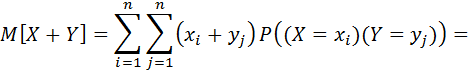
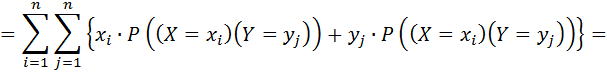
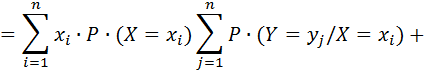
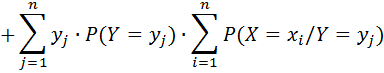
Оскільки поді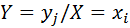ї і 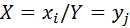– несумісні і єдиноможливі, тоді:

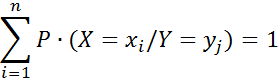
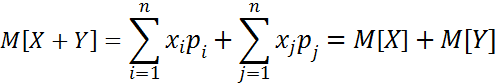
Наслідок.

Властивість 3 можна поширити і на більшу скінчену кількість доданків.

Означення.

ВВ [X₁;...;X_n] називаються взаємозалежними, якщо закон розподілу кожної з них не залежить від того, які можливі значення набувають інші ВВ.

Якщо X і Y – незалежні випадкові величини, тоді: 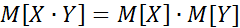. Доведення:

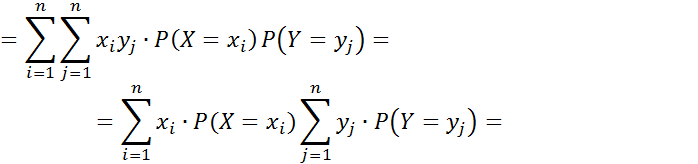
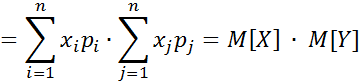
Дисперсія випадкової величини

Дисперсія є мірою розсіювання випадкової величини відносно її середнього значення.

Якщо X – ДВВ одновимірна із законом розподілу 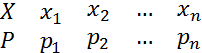, тоді дисперсією Х називають число D[X] рівне математичному сподівання квадрату відхилення випадкової величини від свого математичного сподівання:

D[X] = M [(X – M[X])²]

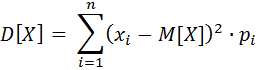
Якщо Х – НВВ, тоді:

Властивості:

1) Дисперсія не буває від’ємною: D[X]≥0

2) Якщо C=const (невипадкова величина), то D[C]=0.

3) D[C∙X] = C² ∙ D[X]

4) Для дисперсії справедлива рівність:

D[X] = M[X²] – M²[X]

D[X] = M[(X - M[X])²] = M[X² – 2 ∙ X ∙ M[X] + M²[X]] =

= M[X²] – 2 ∙ M[X] ∙ M[X] + M²[X] = M[X²] – M²[X].

5) Якщо X і Y – незалежні ВВ, тоді дисперсія суми таких випадкових величин дорівнює сумі їх дисперсій, тобто:

D[X+Y] = D[X] + D[Y]

Остання властивість поширюється на більшу скінчену кількість доданків. Середнім квадратичним відхиленням Х називають число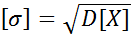

Початкові і центральні моменти ВВ

Означення. Початковим моментом порядку k випадкової величини Х називають число рівне 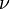_k = M[X^k]

Якщо Х – ДВВ, тоді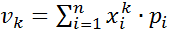

Якщо Х – НВВ, тоді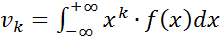

Означення. Центральним моментом порядку k випадкової величини Х називають число рівне μ_k = M[(X – M[X])^k]

Якщо Х – ДВВ, тоді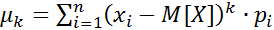

Якщо Х – НВВ, тоді

Очевидні рівності: 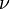₁ = M[X]; μ₁ = M[X-M[X]]=M[X] – M[X]=0

μ₂ = M[(X – M[X])²] = D[X]

Тому початкові і центральні моменти вищих порядків є узагальненими числовими характеристиками ВВ.

До числових характеристик також відносять моду і медіану ВВ.

Модою ВВ називається те її можливе значення, яке має найбільшу ймовірність.

Медіаною ВВ (M_e) називають число:

P(X < M_e) = P(X > M_e)

Дата добавления: 2015-10-23