Сравнение карт разной тематики с целью установления взаимосвязей между явлениями

Анализ и количественная оценка внутренних и внешних связей и взаимозависимостей между геосистемами, их подсистемами и отдельными компонентами – одна из центральных задач в науках о Земле. В их решении картографическому методу принадлежит коронная роль благодаря наличию большого количества карт разной тематики. По ним удобно оценивать изменчивость связей в пространстве, выделять основные и второстепенные зависимости, а также выполнять индикационные исследования, т.е. предсказывать размещение одних (индицируемых) явлений по другим (индикаторам).

Для изучения взаимосвязей используют широкий арсенал технических приемов. Самые простые среди них – визуальный анализ и описание взаимосвязей. Из графических приемов эффективно совмещение контуров анализируемых явлений на общей основе –

графический оверлей, в результате чего выявляются совпадающие, частично совпадающие совсем несовпадающие контуры. Они трактуются как отражение взаимосвязей различной силы.

Многие зависимости наглядно видны на комплексных профилях и разрезах, на совмещенных розах-диаграммах, составленных по серии карт, а также на блок-диаграммах и метахронных диаграммах. Конечно, наилучшие возможности для изучения и количественной оценки взаимосвязей явлений представляет аппарат теории корреляции и информационный анализ: коэффициенты корреляции, показатели взаимного соответствия и др.

При сравнении карт связь явлений всегда проявляется через соответствие картографических изображений. Однако предположение о том, что чем больше степень совпадения контуров или сходство рисунков изолиний, тем сильнее зависимость между явлениями, не всегда справедливо. Случается, что пространственные соответствия можно наблюдать и между явлениями, не зависимыми или очень слабо зависимыми между собой. Поэтому только географический анализ причинно-следственных связей позволяет окончательно судить о реальных зависимостях между явлениями.

При исследовании геосистем важнейший момент составляет прослеживание изменение связей по территории, от места к месту, выявление зон, где связи сильны и где они ослабевают или совсем отсутствуют. Для этого создают специальные карты взаимосвязей, отражающие их пространственное варьирование. В зависимости от способа построения получают разные типы карт:

• Карты районирования по степени взаимного соответствия, составляемые путем географического оверлея и оконтуривания районов полного и частичного соответствий;

• Картограммы взаимосвязей, где показатели корреляции рассчитаны по единицам территориального деления, обычно по административным районам;

• Карты изокоррелят, на которых проведены изолинии равных коэффициентов корреляции по данным, вычисленным в ячейках регулярной сетки;

• Карты энтропии контуров, на которых взаимное соответствие явлений оценивается с помощью показателя энтропии для каждого отдельного контура, ареала, ландшафтного выдела, водосборного бассейна.

Чем подробнее и детальнее показано варьирование от места к месту, тем интереснее карта для пространственного анализа.

82) Кривизна линий и поверхностей

Линия кривизны. Линией кривизны на поверхности называется такая линия на поверхности, у которой в каждой ее точке касательная направлена по главному направлению. Так как в каждой точке поверхности имеются два главных направления, то мы будем иметь два семейства линий кривизны на поверхности, и эти семейства будут взаимно ортогональны. Таким образом совокупность всех линий кривизны даст некоторую ортогональную сетку поверхности.

Элементы теории поверхностей.

Можно определить линии кривизны след образом: рассмотрим на поверхности некоторую линию (L). Нормали к поверхности вдоль этой линии образуют семейство прямых с одним параметром, определяющим положение точки на (L), и это семейство не будет иметь огибающей, ибо вообще семейство прямых в пространстве, зависящее от одного параметра, не имеет огибающей, т.е. не является семейством касательных к некоторой линии в пространстве. Но если выбрать (L) определенным образом, то огибающая нормалей будет существовать. Выясним условия, при которых это имеет место.

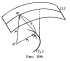
Положим, что линия (L) на поверхности выбрана так, что огибающая (L1) нормалей к поверхности вдоль линии (L) существует (рис 109). Обозначая через r – радиус-вектор точек кривой (L), через r1 – соответствующий радиус-вектор (L1) и через а-алгебраическую величину отрезка нормали к поверхности между (L) и (L1), мы можем, очевидно написать

R1=r+am

Дата добавления: 2015-10-23