Визначити матрицю коефіцієнтів повних матеріальних витрат

(2 спосіб наближений):

а) запишемо матрицю коефіцієнтів непрямих витрат 1-го порядку А²

та матрицю коефіцієнтів непрямих витрат 2-го порядку А³.

Таким чином, матриця коефіцієнтів повних матеріальних витрат приблизно дорівнює:

B» E + A + A² + A³.

Як бачимо елементи матриці В, обрахованої за першим, більш точним способом, є більшими за елементи матриці, обрахованої другим (наближеним) способом.

Знайдемо величини валового ресурсу трьох країн (вектор Х), використовуючи формулу (3) та матрицю коефіцієнтів повних матеріальних витрат, обраховану першим способом:

X = BY

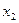де -? (валовий ресурс США), -? (валовий ресурс ЄС),

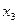-? (валовий ресурс НІК).

Завдання 3.

Для організації передвиборної кампанії кандидата у президенти територія країни була поділена на чотири регіони: Західний, Східний, Південний, Північний.

З метою підвищення рейтингу кандидата на посаду президента планується у кожному регіоні провести наступні заходи::

n розповсюджувати плакати;

n проведення реклами на TV;

n проведення реклами на радіо;

n проведення зустрічей з виборцями.

Соціологічні дослідження свідчать, що:

а) кожні 100 плакатів збільшує рейтинг кандидата у кожному регіоні (в %)

Західний - 1.5; Східний - 2; Південний - 3; Північний - 2);

б) кожні 60 хвилин реклами на TV збільшує рейтинг кандидата у кожному

регіоні (в %) (Західний - 2; Східний - 1.5; Південний - 4; Північний - 3.5);

в) кожні 120 хвилин реклами на радіо збільшує рейтинг кандидата у

кожному регіоні (в %) (Західний - 2.5; Східний - 1; Південний - 3.5;

Північний - 2);

г) кожні 10 зустрічей з виборцями збільшує рейтинг кандидата у кожному

регіоні (в %) (Західний - 1.5; Східний - 2; Південний - 3; Північний - 2).

Після проведених заходів очікується підвищити рейтинг в регіонах:

Західний на 20%; Східний - 15%; Південний - 50%; Північний - 25%.

Визначити скільки всього треба підготувати плакатів у кожному регіоні? Скільки всього необхідно замовити часу на рекламу TV та радіо у кожному регіоні? Скільки всього необхідно провести зустрічей з виборцями у кожному регіоні?

Розв’язати систему рівнянь:

1. Методом (правилом) Крамера.

2. Методом оберненої матриці.

Завдання 4.

В телекомпанії «Інтер» існує інформаційна програма «Вісті». На програмі працює чотири категорії працівників:

- редактори;

- ведучі;

- режисери;

-телеоператори.

Касир кампанії приготував для працівників інформаційних вістей заробітну платню за один тиждень роботи у купюрах наступної вартості: по 20 грн.,

50 грн., 100 грн., 200 грн.. Розподілення купюр буде виражено матрицею

C_{4 ´ 4} з попереднього індивідуального завдання (тема 3). Кількість купюр буде встановлено вектором В, який отримано з співвідношення (сума за рядками матриці С):

b_i = , (n = 4).

Відповідно Вашим таблицям розподілення встановити заробітну плату по кожній категорії.

Визначити, скільки співробітників кожної категорії працює над програмою?

Таблиця

Вартість	Розподілення купюр за категоріями	Загальна
купюри в грн.	редактори	ведучі	режисери	телеоператори	кількість купюр
	?	?	?	?	?

Нехай X = { x₁, x₂, x₃, x₄} - працівники різних категорій, тобто x₁ - редактори; x₂ - ведучі; x₃ - режисери; x₄ - телеоператори. За даними таблиці скласти систему чотирьох рівнянь з чотирма невідомими:

Запишемо систему рівнянь у матричній формі АХ = В.

Розв’язати систему рівнянь:

3. Методом Гаусса.

4. Методом Гаусса - Жордано.

Дата добавления: 2015-10-29