Балансова модель

Тема. Алгебра матриць. Числові методи розв‘язування рівнянь, систем

алгебраїчних рівнянь

Індивідуальні завдання для самостійної роботи студентів.

Завдання 1.

З чисел, що лежать в діапазоні 0 – 9, матрицю В розміром 3´ 3;

· Записати матрицю С розміром 4 ´ 4 яка буде складатися з чисел:

- перший рядок - дата народження;

- другий рядок - рік народження;

- третій рядок - дата виконання роботи;

- четвертий рядок - рік виконання роботи.

· Обчислити детермінант матриці C:

- методом розкладу за елементами будь-якого рядка;

- методом розкладу за елементами будь-якого стовпця;

- за схемою єдиного поділу.

· Обчислити обернену матрицю В ^{– 1} :

- методом приєднаної матриці.

· Обчислити обернену матрицю C ^{– 1} :

- методом виключення.

Завдання 2.

Балансова модель

Під балансовою моделлю слід розуміти систему рівнянь, які задовольняють вимоги відповідності наявності ресурсу (продукції виробництва) та його використання.

Балансові моделі відносяться до типу економіко-математичних моделей, які отримали назву матричних.

Розглянемо балансову модель для трьох суб’єктів: США, ЄС та НІК (Нові індустріальні країни як і країни Європейського Союзу будемо розглядати як окремі неподільні суб’єкти міжнародних інформаційних відносин, надалі просто Країни). Ресурсом для трьох країн виступатиме інформаційний ресурс, що є продуктом інтелектуальної діяльності найбільш кваліфікованої й творчо активної частини працездатного населення тієї чи іншої країни. Інформаційні ресурси виступатимуть в моделі як сукупність інформації, що використовується в усіх сферах людської діяльності. Кожна країна фігуруватиме в балансі як та, що “виробляє” ресурс та “споживає” його.

В основу балансової моделі покладено поділ ресурсу на кінцевий та валовий. Під кінцевим ресурсом (Y) розуміється ресурс, що виходить із сфери виробництва у сферу кінцевого використання (на споживання чи накопичення). Валовий ресурс (X) тієї чи іншої країни дорівнює сумі матеріальних витрат споживаючих її ресурс країн та кінцевого ресурсу даної країни.

Основу інформаційного забезпечення балансової моделі складає матриця (А), яка містить коефіцієнти прямих матеріальних витрат на вироблення одиниці продукції – ресурсу. Коефіцієнт прямих матеріальних витрат показує, яку кількість ресурсу і- ої країни необхідно, якщо враховувати тільки прямі витрати, для виробництва одиниці ресурсу j-ої країни. Враховуючи вектор – стовпець валового ресурсу Х та вектор – стовпець кінцевого продукту У отримаємо наступну систему рівнянь в матричній формі:

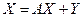(1)

Вищенаведена система рівнянь називається моделлю Леонтьєва чи економіко-математичною моделлю міжгалузевого балансу (замість галузей виступають країни).

За допомогою цієї моделі приступимо до здійснення підрахунків. Задавши величини кінцевого інформаційного ресурсу всіх країн () можна визначити величини валового ресурсу кожної країни ():

(2)

У формулі (2) Е означає одиничну матрицю n-го порядку, а означає матрицю, що є оберненою до матриці (Е-А). Позначимо цю зворотну матрицю В () і запишемо наступну систему рівнянь у матричній формі:

Х = ВY. (3)

Коефіцієнти називаються коефіцієнтами повних матеріальних витрат та вміщують в себе як прямі так і непрямі витрати.

Для трьох країн задано матрицю коефіцієнтів прямих матеріальних витрат та вектор кінцевого ресурсу:

; .

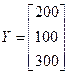Знайдемо коефіцієнти повних матеріальних витрат та вектор валового ресурсу.

Дата добавления: 2015-10-29