Numerical investigations on physical limits of resolution of travel time seismic tomography

Shishkina M.¹, Fokin I.², Akopova S.¹

¹ Lomonosov Moscow State University, Geological Department; ² Institute of the Physics Earth RAS, Moscow, Russia

[e-mail]

Seismic tomography, based on travel time theory of wave propagation, is one of the most common techniques to explore the Earth interior at different scales. This method is based on the conception of infinite large frequency of sounding signal, which literally means that the wavelength is small in comparison to representative size of heterogeneities. Physical limit of resolution power of travel time tomography is approximately equal to the diameter of the first Fresnel zone, which may be estimated as h = (1/2)* 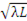, where λ –wave length, L – length of ray.

However, the target heterogeneities have often on practice the size close to the h. For example, during engineering geophysical investigations using sparker source of seismic signals, h can be of 3-4 meters, while target objects can be represented by karst cavities of 1-3 meters. That’s why it’s actual to set numerical experiments to investigate the possibility of detection such objects by travel time tomography as well as shortcomings, appeared during application of this techniques. This represents the basic idea of this work.

The research is done on the basis of simulation numerical modeling with parameters, typical to engineering geophysical investigations. 2D simulation model represents the velocity anomaly in the form of cylinder, located in the inter-well media.

On the first stage the calculation of the times of wave propagation was held on the base of travel time theory using finite-difference solving of Eikonal equation. Than with the help of acquired simulation data the inverse problem of travel time seismic tomography was solved using algorithm [1]. The solution result refracts the configuration of simulation model correctly.

On the second stage the series of experiments were done, where the wave propagation was modeled by the method of spectral elements [2] for the number of wave lengths – such, that the Fresnel zone radius changes from the values much less the size of heterogeneities in the model to the values, much greater than this size. In every case the first arrivals of primary wave were defined and the inverse seismic problem of travel time tomography was solved using times of these arrivals. The parameters were the same as on the first stage. The analyses of these solutions let us estimate the practical capabilities and restraints of travel time seismic tomography in the engineering geophysical investigations.

References:

1. Тихоцкий С. А., Фокин И. В., Шур Д. Ю. Активная лучевая сейсмическая томография с использованием адаптивной параметризации среды системой вэйвлет-функций // Физика Земли. 2011. No 4. С. 67–86.

2. Komatitsch, D. and Vilotte, J.-P. The spectral element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures // BSSA, 1998. Vol. 88, No. 2, pp. 368-39.

3. Nolet G. A Breviary of seismic tomography. Cambridge Univ.Press, 2008. P. 344.

Дата добавления: 2015-10-29