Crystal lattice

When the atoms draw near, between atoms exist the forces of the interaction. Figure 2.1 shows the dependence of the energy of the interaction and the dependence between them.

It means, that the atoms in crystal lattice must be in equilibrium state, when r near to r.

Then we may to make the conclusion that the atoms must construct in the strict order under influence the forces of the interaction. In result it formed a body with regularity or periodically structure. So bodies are crystals. For describing crystal structure we use the idea of the crystal lattice.

Curve 1: When r > r₀ between the atoms there are the forces of the attraction.

Curve 2: When r tends r₀ (r => r₀) between the atoms began to act the repellent forces.

Curve 3: When r = r₀, then F _att= F _rep, and so the energy of the interaction reaches

minimum U _min how it shows " b ".

Figure 2.1

The crystallization process of a substance occurs due to the forces of attraction acting between its particles. At small his dances disappear and the forces of repulsion appear, preventing the further binding of particles. These forces strive to arrange the particles of substance as closer to each other as possible. In the first approximation we may to compare molecules with solid particles, in particular, with balls of definite radius witch may be brought only into contact by the forces of attraction.

When ball-type particles are packed tightly, each of them is surrounded by a certain number of adjoining (neighboring) particles arranged at equal distances from the first. This number is called a coordination number with values 12, 8, 6, 4 and 2.

The orderly distribution of particles within the volume of a crystal forms co called space crystal lattice. Geometrically the entire pattern of a lattice can be obtained if we draw three systems of planes intersecting between themselves at angles and. The planes in each system are parallel to each other and are spaced at equal distances a, b and c. These planes divide the crystal by unit cells constituting kind of bricks of witch the whole crystal is built. Depending on the ratio between the cell ribs a, b and c as well as the angles we distinguish seven crystallographic systems:

a) a = b = c; α = β = γ = 90⁰ – cubic system;

b) a = b ≠ c; α = β = 90⁰, γ = 120⁰ – hexagonal system;

c) a = b ≠ c; α = β = γ = 90⁰ – tetragonal system;

d) a ≠ b ≠ c; α = β = γ = 90⁰ – trigonal system;

e) a ≠ b ≠ c; α = β = 90⁰ ≠ γ – monoclinic system;

f) a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90⁰ – triclinic system;

g) a = b = c; α = β = γ ≠ 90⁰ – rhombohedral system.

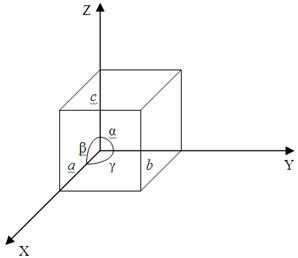
Figure 2.2

Дата добавления: 2015-10-29