Формула Стокса.

Наведемо без доведення величину сили опору F кульці радіуса r, що рухається в рідині зі сталою швидкістю u

.

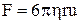Ця формула називається формулою Стокса.

8.7. Тверде тіло

Тверде тіло ¾ тіло, яке має сталі форму й об'єм. Тверді тіла поділяються на кристалічні та аморфні.

Кристали ¾ тверді тіла, що мають у всьому об’ємі правильне періодичне розташування частинок (дальній порядок, кристалічна решітка).

Монокристали ¾ кристали, що мають форму правильних многоогранників. Фізичні властивості кристалів (механічні, теплові, електричні, оптичні) залежать від напрямку (є анізотропними). Полікристали мають дрібнозернисту структуру, створену великим числом хаотично розташованих моно кристаликів. Більшість твердих тіл у природі є полікристалами. Їх фізичні властивості не залежать від напрямку і вони є ізотропними.

Аморфні тілане мають кристалічної решітки, вони ізотропні, являють собою переохолоджену рідину. Типовим прикладом аморфного тіла є скло. Кристалічна решітка може мати різні симетрії. Симетрія¾ властивість решітки співпадати із самою собою при деяких просторових переміщеннях чи поворотах. Операції повороту навколо осі на кути 2p/n_і, віддзеркалення від площини, трансляції (переміщення вздовж певного напрямку) та їх комбінації, що суміщають кристал сам із собою називаються операціями симетрії, а осі поворотів, напрямки трансляції, площини та точки віддзеркалення і їх комбінації називаються елементами симетрії.

Основу кристалічної структури створює елементарна комірка, повторення якої у трьох напрямках простору створює даний кристал. Така комірка являє собою паралелепіпед, побудований на трьох векторах 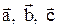із відповідними кутами ¾ кут між векторами , b ¾ кут між векторами 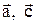, g ¾ кут між між векторами . Вектори 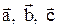називаються періодами решітки. Кристалічна комірка, яка містить мінімальне число атомів, що характеризують хімічний склад кристала, називається примітивною. Симетрія елементарної комірки задає симетрію кристалів і розподіл їх по групам і класам.

За Є. С. Федоровим у природі можливі 230 комбінацій елементів симетрії, які називають просторовими групами. Просторові групи розподіляються на 32 класи. За формою елементарної комірки всі кристали розподіляються на сім кристалографічних систем (сингоній). Сингонії за типами розподіляються на системи, представлені на Мал.67.

1.

Триклинна система: похилий паралелепіпед.

2. Моноклинна система: основа паралелепіпеда і 2 протилежні грані прямокутники.

3. Ромбічна система: прямокутний паралелепіпед.

4. Тетрагональна система: прямокутний паралелепіпед з квадратом в основі.

5. Тригональна система: прямий паралелепіпед з ромбом в основі.

6. Гексагональна система: пряма призма з правильним шестикутником в основі.

7. Кубічна система має елементарну комірку у вигляді куба.

Зауваження. Нагадаємо визначення призми. Многогранник, дві грані якого - рівні n-кутники з відповідно паралельними сторонами, а всі інші n граней паралелограми, називається n-кутною призмою. Її рівні n-кутники називаються основами, а паралелограми - бічні грані. Ребра призми, що не є сторонами основ, називаються бічними. Якщо бічні ребра перпендикулярні основам - призма пряма. Призма, в основі якої лежить паралелограм, називається паралелепіпедом. Паралелепіпед називається прямокутним, якщо усі його грані прямокутники.

8.7.1.Анізотропія кристалів

Як указувалося вище, основною відмінністю від ізотропних тіл, є те, що кристали мають анізотропні властивості. Вони полягають у тому, що фізичні властивості кристалів залежать від напрямку. Наприклад, у ізотропному діелектрикові вектор електричної індукції (зміщення) зв'язаний з вектором напруженості електричного поля 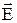лінійним рівнянням . Це означає, що 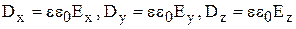. У кристалі цей зв'язок набуває іншого характеру

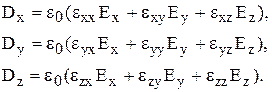(1)

У цьому випадкові кажуть що між та 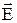існує тензорна залежність через тензор діелектричної проникливісті

. (2)

Фізичний зміст (1) полягає у тому, що кожна з компонент індукції лінійно залежить від усіх компонент електричного поля.

8.8. Фізичні типи кристалів

В залежності від природи частинок у вузлах кристалічної решітки й характеру взаємодії між частинками розрізнюють чотири типи кристалів: іонні, атомні, металічні й молекулярні.

1. Іонні кристали (NaCl, KCl та інші). У вузлах решітки розміщені іони різних знаків заряду. Сили взаємодії ¾ електростатичні (кулонівські) сили тяжіння між різнойменно зарядженими іонами. Такий зв'язок називається гетерополярним. Примітивна решітка іонного кристала кухонної солі представлена на Мал.68 а.

2.Атомні кристали (алмаз, графіт, ZnS і т. п.). У вузлах решітки розміщені нейтральні атоми. Зв'язок між атомами має квантову природу і називається гомеополярним (або ковалентним). Зв'язок здійснюється парами валентних електронів взаємодіючих атомів, що визначає направленість їх взаємодії. Примітивна решітка ковалентного кристала алмаза представлена на Мал.68 б.

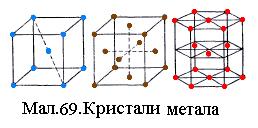3. Металічні кристали. У вузлах решітки розміщені додатні іони металів, між якими хаотично рухаються вільні валентні електрони, що відокремились від атомів при утворенні іонів. Ці електрони утримують додатні іони у вузлах. Сили зв'язку визначаються взаємодією іонів із газом вільних електронів та квантовими обмінними силами перекриття внутрішніх електронних атомних орбіталей. Більшість металів має примітивні решітки одного з трьох типів, представлених на Мал.69: об'ємноцентровану, гранецентровану та повну гексагональну.

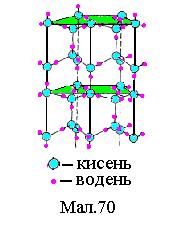4.Молекулярні кристали (H₂, N₂, O₂, CO₂, H₂O і т. п.). У вузлах решітки розміщені певним чином орієнтовані молекули. Сили зв'язку між молекулами в кристалі називаються ван-дер-ваальсовими і вони мають ту ж природу, що і сили тяжіння між молекулами реального газу. Примітивна решітка молекулярного кристала льоду представлена на Мал.70.

8.9. Теплове розширеннята теплоємність кристалів

Тверді тіла при нагріванні розширюються, а їхні лінійні розміри L змінюються за законом

,

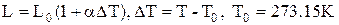де температурний коефіцієнт лінійного розширення, ¾ початкова довжина при , 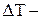приріст температури. Відповідно змінюється й об'єм твердого тіла

,

де 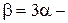температурний коефіцієнт об'ємного розширення, V₀ ¾ об'єм при .

Тверде хімічно просте кристалічне тіло з класичної точки зору являє собою одну молекулу з N атомами, яка має 3N - 6» 3N коливальних ступенів свободи. На них приходиться теплова енергія коливального руху U = 3NkT. У зв'язку з малістю коефіцієнта теплового розширення можна вважати, що теплоємності при сталому об'ємі і сталому тискові рівні між собою і тоді для високих температур (для більшості твердих тіл кімнатна температура є вже досить високою)

.

Для моля речовини кристала і

.

Такий результат збігається з експериментально встановленим правилом Дюлонга - Птідля високих температур кристала. Теплоємність твердих тіл, які не є хімічно простими, дорівнює сумі атомних теплоємностей елементів, що складають речовину. Наприклад, молярна теплоємність кухонної солі дорівнює .Нижче в таблиці наведені експериментальні значення молярних теплоємностей деяких твердих тіл.

Таблиця. Теплоємність деяких твердих тіл

Речовина	С, Дж/(моль-К)
теорія	дослід
Алюміній А1		25,5
Алмаз С		5,9
Берилій Be		15,6
Бор В		13,5
Залізо Fe		26,8
Срібло Ag		25,6
NaCI		50,6
AgCl		50,9
СаСl2		76,2

Як показують наведені в таблиці дослідні дані, для багатьох речовин закон Дюлонга й Пті виконується задовільно, хоча теплоємності С,Be, В мають значні відхилення.

Досліди по вимірюванню теплоємностей твердих тіл при низьких температурах показали, що вони залежать від температури пропорційно . Для хімічно простих речовин хорошу модель розрахунку теплоємності створив на основі квантової теорії П. Дебай. Температурна залежність теплоємності за Дебаєм представлена на Мал.25. У цій моделі теплоємність при низьких температурах кристалів визначається законом Дебая

,

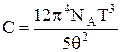де 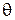¾ характеристична температура Дебая. Дослідні та експериментальні значення теплоємностей для хімічно простих речовин практично мають незначні розбіжності. При температурах більших за характеристичну температуру Дебая теплоємність кристалів розглядається на основі класичної теорії, а при нижчих ¾ на основі квантової теорії.

8.10. Фазові перетворення

На представленій на Мал.71 фазовій діаграмі зображені процеси можливих фазових перетворень при зміні температури речовини. При підвищенні температури твердого тіла, відбуваються фазові перетворення 1¾2: кристал із твердої фази 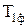перетворюється у тверде тіло з іншою фазою 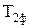і далі в рідину Р ¾ процес плавлення, а рідина в газ Г ¾ процес випаровування. При пониженні температури відбувається зворотній процес 2¾1: газ конденсується в рідину, а рідина кристалізується у тверде тіло. Процес плавлення (кристалізації) відбувається при сталій температурі рівній температурі плавлення, а конденсація ¾ при температурі рівній температурі кипіння. Крім указаного існує процес 3¾4 сухого випаровування (сублімації) твердого тіла 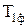без переходу його в рідину. У твердих тілах, рівно як і у рідинах, є деяке число молекул, теплова енергія яких достатня для подолання тяжіння до інших молекул і які здатні відірватися від поверхні твердого тіла чи рідини і перейти в навколишній простір. Цей процес для твердих тіл — називається сублімацією. Для більшості твердих тіл процес сублімації при звичайних температурах незначний і тиск пари над поверхнею твердого тіла малий. Інтенсивно сублімують такі речовини, як нафталін, камфора, що виявляється по різкому, властивому їм запаху. Особливо інтенсивно сублімація відбувається у вакуумі — цим користуються для виготовлення дзеркал. Відомий приклад сублімації льоду — мокра білизна висихає на морозі.

На діаграмі P ¾ Т стан речовини розділяється кривими фазової рівноваги, які пересікаються в одній точці 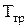. Ця точка називається потрійною. В точці 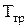речовина знаходиться в рівновазі одночасно у твердій, рідинній та газовій фазі. Крива називається кривою сублімації, крива 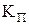називається кривою плавлення, крива 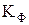називається кривою фазового переходу, крива називається кривою випаровування, яка закінчується в точці К, що визначається критичною температурою. Завдяки існуванню критичної точки К можливий неперервний перехід рідини у газ 5-6. Крива плавлення не має кінцевої точки, як це є у кривої випаровування. Розглянуті переходи відбуваються з виділенням чи поглинанням тепла і називаються фазовими переходами.

На діаграмі показані фазові стани речовини, які співпадають власне з агрегатними станами. Проте існують різні модифікації твердого тіла, що мають різні симетрії. Такі стани мають один агрегатний стан ¾ наприклад, тверде тіло, але різні фази. Переходи твердого тіла або рідини з одної фазової модифікації, наприклад, 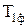в 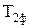із зміною внутрішньої симетрії називаються фазовими переходами 2-го роду. Вони відбуваються без поглинання чи виділення тепла.

8.11. Контрольні питання

1. Які гази називають реальними.

2. Представте ізотерми реальних газів на P-V діаграмі.

3. Опишіть критичний стан на діаграмі P-V.

4. Визначте поняття пару.

5. Визначте поняття насиченого пару.

6. Який фізичний зміст має критична опалесценція?

7. Опишіть рівняння Ван - дер - Ваальса.

8. Представте на P-V діаграмі ізотерми Ван - дер - Ваальса.

9. Визначте зв'язок сталих Ван - дер - Ваальса та критичних араметрів.

10. Виведіть величину внутрішньої енергії реального газу.

11. Опишіть фізичні властивості рідини.

12. Визначте ближній порядок та час релаксації рідини.

13. Введіть поняття потенціальної енергії поверхневого натягу рідини.

14. Введіть поняття сили поверхневого натягу рідини.

15. Охарактеризуйте процес змочування рідини.

16. Визначте крайовий кут змочування рідини.

17. Скривлення поверхневого шару рідини та рівняння Лапласа для додаткового тиску.

18. Виведіть висоту підйому рівня рідини в капілярі.

19. Опишіть процес кипіння рідини.

20. Опишіть об'ємне розширення рідини.

21. Опишіть процес випаровування рідини.

22. Дайте поняття абсолютної та відносної вологості повітря.

23. Точка роси.

24. Запишіть розподіл швидкості рідини у циліндрі.

25. Виведіть формулу Пуазейля.

26. Запишіть формулу Стокса.

27. Опишіть фізичні властивості твердого тіла.

28. Кристали та монокристали.

29. Аморфні тіла.

30. Опишіть кристалічну решітку.

31. Дайте поняття елементарної комірки.

32. Дайте поняття примітивно комірки.

33. Що являють собою атомні кристали?

34. Що являють собою металічні кристали?

35. Що являють собою молекулярні кристали?

36. Класична теорія теплоємності кристалів.

37. Правило Дюлонга - Пті

38. Визначте поняття фазових переходів І та ІІ родів.

39. Що означає потрійна точка фазових переходів?

40. Опишіть криву сублімації.

41. Опишіть криву плавлення.

42. Опишіть криву випаровування.

Дата добавления: 2015-10-29