Формула Пуазейля.

Змочування

Змочуванням називається явище взаємодії рідини з твердим тілом і газом на границі розділу трьох фаз, коли вільна поверхня рідини коло твердої поверхні скривлюється. Така скривлена поверхня рідини називається меніском і характеризується крайовим кутом J між змоченою поверхнею твердого тіла й меніском рідини в точках їх пересічення (див.Мал.63). Мірою змочуванняє величина кута J, що визначається з рівняння рівноваги елементарного одиничного (dl=1) контуру на границі розділу фаз

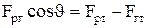, (6)

або

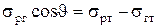, (7)

де коефіцієнти поверхневого натягу на трьох поверхнях розділу фаз. Наведена на малюнку поверхня рідини має місце лише при

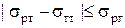. (8)

Якщо

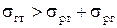, (9)

то спостерігається явище повного змочування ¾ рідина розтікається по всій поверхні твердого тіла. Сила s_тг перевищує дві інші і крайовий кут 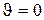. Якщо сила

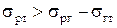, (10)

то спостерігається явище повного незмочування, .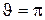

8.3.2. Тиск під скривленою поверхнею

Скривлення поверхневого шару рідини призводить до появи додаткового тискуна рідину, який визначається рівнянням Лапласа

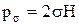, (11)

де

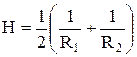(12)

середня кривизна поверхні, i головні радіуси кривизни поверхні, що визначаються радіусами кривизни ліній нормального перетину двох взаємно перпендикулярних площин із поверхнею. Наприклад, для циліндричної поверхн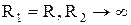і і 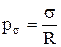; a для сфери 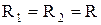і

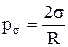. (13)

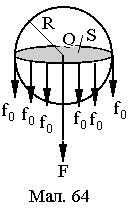
Іншим шляхом вираз (13) можна одержати з таких міркувань. Розглянемо уявну рідину у формі сфери радіуса R. Проведемо через центр сфери січну площину (див.Мал.64). В результаті одержимо дві півкулі з площею основ 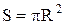та зовнішнім контуром контакту довжиною 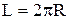. Півкулі взаємодіють між собою лише вздовж контуру із силою , перпендикулярною до S. Ця сила створює на поверхню розділу S тиск

,

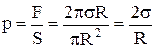що й треба було довести.

8.4. Капілярні явища

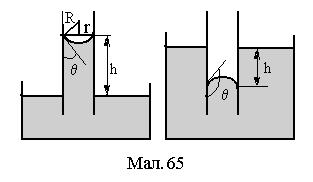
У вузьких циліндричних судинах (капілярах) радіуса r рівень рідини, що змочує (не змочує) поверхню судини вище (нижче) ніж у широкій судині, сполученій з капіляром, на величину

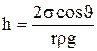, (1)

де 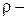густина рідини, 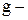прискорення сили тяжіння, 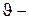крайовий кут змочування (див.Мал.65).

Вираз (1) можна одержати з рівності сили поверхневого натягу та сили тиску рідини в капілярі так. Тиск стовпа рідини висотою h дорівнює

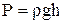. Він врівноважується додатковим тиском під скривленою поверхнею рідини 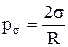. Радіус R можна виразити через кут змочування 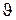та радіус капіляра r (див.Мал.65) так 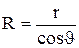. Рівність тисків Р та 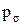дає

,

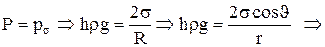
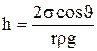що й треба було довести.

8.5. Теплові процеси в рідині

Кипіння ¾ процес інтенсивного випаровування рідини з усього об'єму рідини всередину, утворюваних при цьому, пузирів. При кипінні тиск насичених парів у пузирі дорівнює зовнішньому тискові. Температура, при якій вирівнюються вказані тиски, називається температурою кипіння.

Об'ємне розширення рідини при нагріванні визначається рівнянням

,

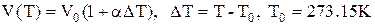де 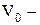об'єм рідини при , 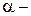коефіцієнт об'ємного розширення рідини, 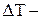приріст температури.

Випаровування ¾ процес пароутворення з вільної поверхні рідини. Насичений пар ¾ пар, що знаходиться в динамічній рівновазі з рідиною.

Для випаровування маси m рідини потрібна теплота

,

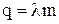де 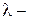коефіцієнт пароутворення. При конденсації маси m пару виділяється теплота

.

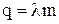Атмосферний тиск ¾ сума парціальних тисків усіх газів, що створюють атмосферу. Тиск, який створює водяна пара 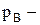парціальний тиск водяної пари або пружність пари. Абсолютна вологість атмосфери чисельно дорівнює масі парів води, що міститься в одиниці об'єму повітря

,

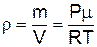де 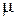= 0.018 кг/моль ¾ молярна маса води.

Точка роси ¾ температура при якій водяні пари, що містяться в повітрі, установляться насиченими і починається їх конденсація.

Відносна вологість ¾ відношення парціального тиску (пружності) 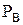водяної пари, яка міститься в повітрі при даній температурі, до тиску (пружності) насиченої пари (точка роси) при тій же температурі заданої у процентах

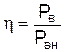×100% або 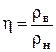×100%,

де 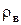й абсолютні вологості повітря при даній температурі і при точці роси.

8.6. Стаціонарна течія рідини та газу в циліндрі

8.6.1.Радіальний розподіл швидкості течії у циліндричному потоці

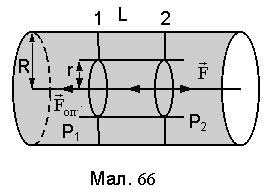1. Знайдемо розподіл швидкості рідини u у циліндрі при стаціонарній течії.Нехай рідина з в’язкістю 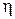протікає в циліндрі радіуса R і довжини L при перепаді тиску на кінцях циліндра 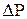(див.Мал.66). Виділимо циліндричну трубку течії радіуса r співвісну циліндру. Рух рідини виділеної трубки току відбувається за рахунок дії сили перепаду тиску на основах трубки 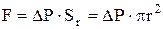. Ця сила долає силу опору 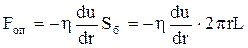, де 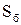¾ бічна поверхня циліндра трубки току. При стаціонарній течії рідини сили тиску та опору врівноважуються

F=F_оп і тоді

.

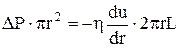З цього рівняння одержимо диференціальне рівняння для визначення радіальної залежності швидкості току u

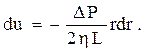
Інтегрування одержаного рівняння дає

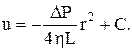
Сталу С визначимо з умови, що швидкість току рідини при стінках циліндра, коли r=R дорівнює 0, тобто

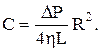
Остаточно, радіальна залежність швидкості току рідини буде такою

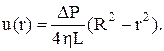
Формула Пуазейля.

Обчислимо об'єм рідини, що витікає через циліндр за час dt. Для цього запишемо об'єм рідини dV, що протікає за dt через основу радіального кільця 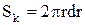при трубці току шириною dr

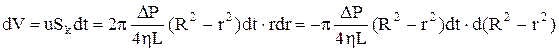
Інтегруючи останній вираз по r від 0 до R, одержимо

.

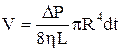Ми одержали відому формулу Пуазейля, за допомогою якої можна визначити об'ємну витрату V газу або рідини з в'язкістю h, що протікає через трубку радіуса R, довжини L при перепаді тисків 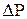на її кінцях за час dt.

За експериментально визначеною величиною витрати V можна знайти величину коефіцієнта в'язкості газу чи рідини

.

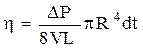Дата добавления: 2015-10-29