Сынған сәуленің поляризациясы. Брюстер заңы.

Тәжірибеге қарағанда, жарық екі ортаның шекарасында шағылғанда және сынғанда азды-көпті поляризацияланады. Жарықтың мөлдір екі диэлектрик орта шекарасында поляризациялануына тоқталайық. Табиғи жарық шоғы прпллель- жазық шыны пластинка бетінен шағылғандағы поляризациялануын қарастырайық. Мысалы, ММ қоңыр шыны пластинканың О нүктесіне і бұрыш жасап түскен SO сәуле одан шағылып жолындағы T₁ турмалин пластинкадан өтетін болсын. Егер осы пластинканы шағылған OS₁ сәулеге дәл келетін осьтен айналдырсақ, шағылған жарық интенсивтігінің өзгергендігін байқаймыз. Егер түсу бұрышы i= 56⁰ болса, турмалин пластинканы толық бір айналдырғанда шағылған жарық интенсивтігі екі рет нөлге теңеледі, яғни жарық екі рет сөнеді.Мұның себебі: шыныдан шағылған жарық поляризацияланған болғаны. Мұнда шыны пластинка поляризатор, турмалин пластинка анализатор болып табылады. Осындай зерттеулер нәтижесінде қарағанда шағылған жарық түсу жазықтығында поляризацияланады, басқаша айтқанда оның электр векторы түзу жазықтығына перпендикуляр жазықтықта тербеледі. Жазық-параллель шыны пластинкадан шағылған жарықтың поляризациялану күйін зерттегенде анализатор етіп екінші жазық- параллель шыны пластинканы алуға да болады. Табиғи жарықтың S₁O₁ сәулесі M₁N₁ жазық-параллель шыны пластинкадан шағылған соң дәл сондай M₂N₂ шыны пластинкаға түсіп, екінші рет шағылсын, жарықтың бұлардан шағылу бұрыштары бірдей (i’=i₁’) болсын, M₂N₂ пластинканы O₁O₂ сәулемен дәл келетін осьтен айналдырғанда одан шағылған жарықтың интенсивтігі өзгереді. Сонда жарықтың M₁N₁ және M₂N₂ пластинкаға түсу жазықтықтары бір-біріне параллель болған жағдайда M₂N₂ пластинкадан шағылған жарықтың интенсивтігі максималь болады, егер сол түсу жазықтықтары өзара перпендикуляр болса, онда шағылған жарық интенсивтігі минималь болады. Бұл жағдайда шағылған жарық толық поляризацияланған болады. Сондағы түсу бұрышы (i₀) толық поляризациялану бұрышы, немесе Брюстер бұрышы деп аталады. Брюстердің 1815ж. тағайындауы бойынша жарықтың толық поляризациялану бұрышының тангенсі жарық шағылатын ортаның жарық сыну көрсеткішіне тең:

tg i₀=n

мұндағы n- салыстырма сыну көрсеткіші. Бұл қорытынды Брюстер заңы деп аталады. Брюстер заңы — диэлектриктің сыну көрсеткіші (n) мен оның бетінен шағылып, толық полярланып шығатын табиғи жарықтың түсу бұрышы (Б) арасындағы қатынас. Брюстер заңы бойынша түсу жазықтығына перпендикуляр болатын жарық толқыны электр векторының ЕS құраушысы ғана (яғни, жарықтың бөліну бетіне параллель құраушысы) шағылады, ал жарықтың түсу жазықтығында жататын ЕР құраушысы шағылмайды, сынады. Брюстер заңын 1815 жылы ағылшын физигі Д. Брюстер (1781 — 1868) ашқан. Дегенмен кейбір арнаулы тәжірибелер Брюстер заңының дәл орындала бермейтінін көрсетті.

Бұл заңды жарық тек диэлектриктер (шыны, кварц, су т.т.) бетінен шағылғанда ғана қолдануға болады. Жалпы, жарық екі мөлдір ортаның шекарасында әрі шағылады, әрі сынады. СОнда шағылған сәуле де сынған сәуле де поляризацияланады. Егер жарықтың түсу бұрышы Брюстер бұрышына тең болса, онда шағылған сәуле толық поляризацияланады, сынған сәуле шала поляризацияланады. Жоғарыда айтылғандай шағылған жарық түсу жазықтығында перпендикуляр жазықтықта поляризацияланады.

Егер жарық толқынларының электр векторы түсу жазықтығына перпендикуляр бағытта тербелсе, яғни жарық түсу жазықтығында поляризацияланған болса, онда шағылу коэффициенті (p_s) мынадай формулпмен өрнектеледі: p_s=sin²(i-r)/sin²(i+r).

Егер жарық толқындарының электр векторы түсу жазықтығында тербелсе, яғни жарық түсу жазықтығына перпендикуляр жазықтықта поляризацияланған болса, онда шағылу коэффициенті (p_р) мынаған тең: p_р= tg²(i-r)/tg²(i+r), мұндағы i,r –түсу және сыну бұрыштары.

Егер түскен жарық поляризацияланбаған болса, онда шағылу коэффициенті (p) мынадай формуламен өрнектеледі: p=1/2[sin²(i-r)/sin²(i+r)+ tg²(i-r)/tg²(i+r)].

Жарық екі диэлектриктің шекара бетіне тік түскен жағдайда шағылу коэффициенті мынаған тең болады: p=(n-1/n+1)²

Мұндағы n- екінші ортаның салыстырма сыну көрсеткіші.Осы келтірілген формулалар диэлектрик бетінен жарық шағылу коэффициенттерін есептеу үшін пайдаланылады.

68. Жарықтың дисперсиясы.

Максвеллдің теориясы бойынша диэлектриктік өтімділік әр затты сипаттайтын тұрақты шама деп саналады. Олай болса заттың сындыру көрсеткіші де тұрақты болуға тиіс.

Бірақ тәжірибеге қарағанда заттың жарық сындыру көрсеткіші жарық толқындарының ұзындығына тәуелді. Мысалы, шынының бір сортының толқын ұзындығы λ=656.3нм, қызыл сәулені сындыру көрсеткіші n=1.5139; толқын ұзындығы λ= 589 нм, сары сәулені сындыру көрсеткіші n=1,5163; толқын ұзындығы λ= 486 нм, көк сәулені сындыру көрсеткіші n=1,5220. Бұдан шынының сыну көрсеткіші көрінетін жарық толқын ұзындығы кеміген сайын арта түсетіндігі байқалады. Бұл кәдімгі мөлдір заттан өткенде күлгін сәуленің жасыл сәуледен гөрі күштірек, жасыл сәуленің қызыл сәуледен гөрі күштірек сынатындығына сәйкес келеді.

Заттың жарық сындыру көрсеткішінің жарық толқыны ұзындығына тәуелділігі жарық дисперсиясы деп аталады. Егер заттың абсолют сыну көрсеткіші n болса, оның толқын ұзындығына (λ-ға) тәуелділігін былай өрнектеуге болады: n=f(λ).

Суретте шынының (1), кварцтың (2) және флюориттың (3) сыну көрсеткіштерінің көрінетін жарық толқындары ұзындығына байланысты қалай өзгеретіндігі кескінделген. Осылай жарық толқындары ұзарғанда, яғни тербеліс жиілігі азайғанда сыну көрсеткіштерінің кемуі қалыпты дисперсия деп аталады.

Жарық толқындары қысқарғанда, яғни тербеліс жиілігі артқанда сыну көрсеткішінің кемуі аномаль дисперсия деп аталады.

Дисперсия құбылысын электрондық теория тұрғысынан қарастырып түсіндіруге болады. Жарық таралған орта атомдарының құрамындағы эдектрондар жарық толқындары айнымалы электр өрісі әсерінен еріксіз тербеле бастайды. Сонда электронға өріс тарапынан әсер еткен күш шамасы, орта біртекті және изотроп болып, толқын монохромат және жазықша поляризацияланған болса, мынаған тең болады: 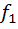=eE=eE₀sinωt. Мұндағы Е₀-өріс кернеулігіні амплитудасы, ω – бұрыштық жиілік, әдеттегіше ω=2πν, мұнда ν-тербеліс жиілігі.

Егер жарық таралған диэлектрик ортаның жарық өрісі ықпалынан тербелетін электрондары бірнеше топқа бөлініп, әр топта N_i электрон болып тербеліс өшпейтін болса, сыну көрсеткіш мына түрде жазуға болады: 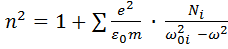. Мұндағы ω_0i – әр топтың меншікті тербеліс жиілігі.

Бұл жағдайда дисперсия қисығы бірнеше бұтаққа тармақталады. Өйткені жарық тербеліс жиілігі әрбір топтың меншікті тербеліс жиілігіне теңелгенде (ω=ω_0i) сыну көрсеткіш мәндері шексіз үлкен болады. (n=±∞).

Дата добавления: 2015-10-29