Surfaces of rotation

Let some curve located in the plane 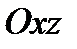have an equation 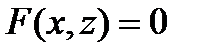. If rotate this curve around the axis 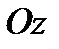then its every point will describe a circumference.

The set of points of which the coordinates satisfy the equation 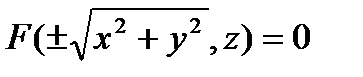is called a surface of rotation.

Example. The following surfaces are surfaces of rotation:

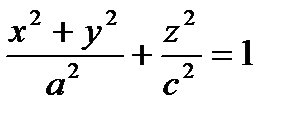– an ellipsoid of rotation (the axis of rotation is ).

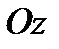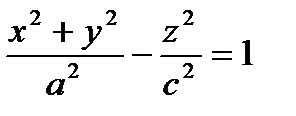– an one-sheeted hyperboloid of rotation (the axis of rotation is ).

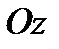Example. Find an equation of the surface obtained at rotating the line 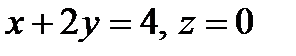around the axis .

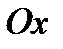Solution: The surface of rotation is the cone with the vertex in the point 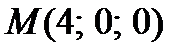. Let an arbitrary point of the required surface have the coordinates 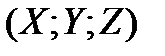. The point 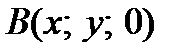on the line is corresponded to . The points and 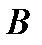lie on one plane that is perpendicular to the axis of rotation 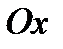. Then 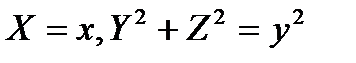. Substituting these expressions in the equation of the line, we obtain the equation of the required surface: 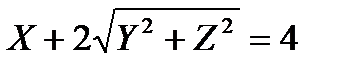or

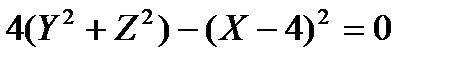, i.e. .

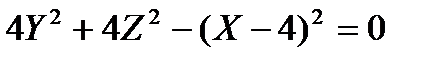Let an orthonormal system of coordinates 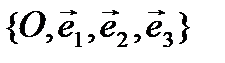be given in the space. We say a surface is called an algebraic surface of the second order if its equation in a given system of coordinates has the form: ,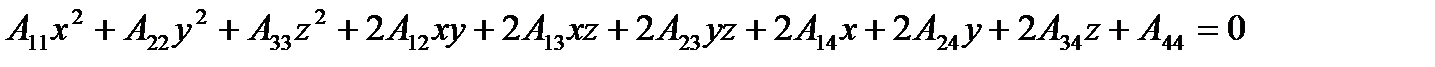

where the numbers 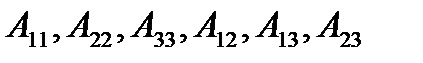are not equal to zero simultaneously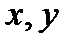, and and 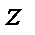are the coordinates of radius-vector of a point lying on a given surface .

Theorem. For every surface of the second order there is an orthonormal system of coordinates 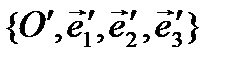in which an equation of this surface has one of the following 17 canonic forms:

Empty sets	Points, lines and planes	Cylinders and cones
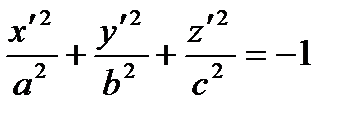
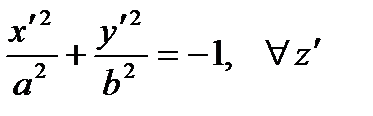
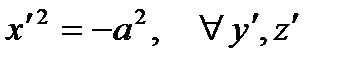
	Isolated point 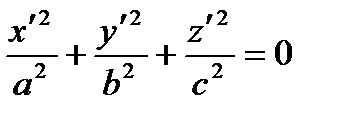Line 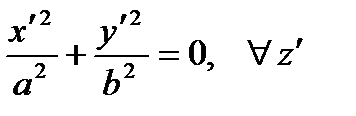Pair of intersecting planes 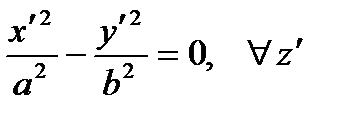Pair of parallel (or coinciding) planes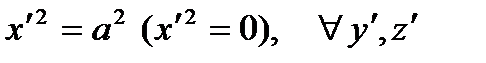	Elliptic cylinder 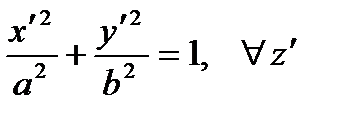Hyperbolic cylinder 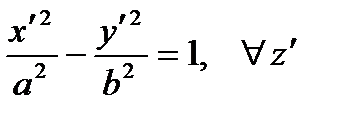Parabolic cylinder 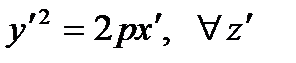Cone

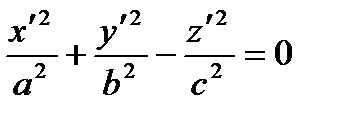
Non-degenerate surfaces
Ellipsoids	Paraboloids	Hyperboloids
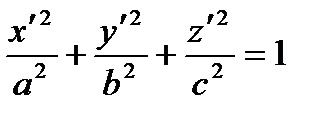
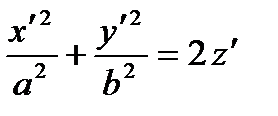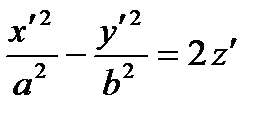
	Elliptic paraboloid Hyperbolic paraboloid	One-sheeted hyperboloid 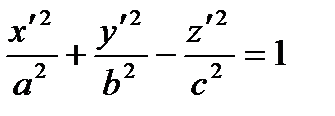Two-sheeted hyperboloid

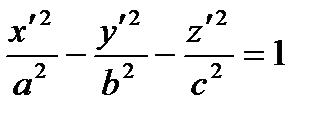
where

Дата добавления: 2015-10-29