Производственная функция. Эффект отдачи от масштаба

Под производством в современной микроэкономике понимается деятельность по использованию факторов производства (ресурсов) с целью достижения наилучшего результата (максимально возможного выпуска или максимальной прибыли).

Обычно в моделировании предполагается, что в процессе производства используются 2 фактора: и 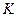. Тогда производственная функция выражает технологическую взаимосвязь между конечным выпуском () и затратами факторов производства и 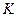. Она записывается следующим образом: , где - форма функции.

- обязательно, максимальный выпуск, который можно получить при заданной технологии и данном количестве используемых факторов производства ( и ).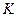

В производственной функции нет экономических параметров, затраты и 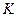измеряются в натуральных единицах (человеко-часах или станко-часах).

Примером производственной функции записанной в явном виде может служить производственная функция Кобба-Дугласа, которая имеет следующий вид: , ,

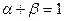где 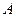- эффективность технологии. Функция Кобба-Дугласа описывает экстенсивный тип производства.

Если в процессе производства используется 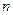- факторов, то производственная функция имеет вид: ,

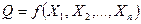где - количество используемого 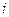-того фактора производства.

Изокванта (или кривая постоянного продукта (isoquant) – график производственной функции; - это кривая, представляющая собой бесконечное множество комбинаций факторов производства (ресурсов), обеспечивающих одинаковый выпуск продукции.

Свойства производственной функции:

1. Производственные факторы являются взаимодополняющими. Это значит, что если один из фактор равен нулю, то и выпуск равен нулю.

Но есть и исключение: , например, грузчик в ходе своей работы может и не использовать капитал.

2. Свойство адитивности. Объединить факторы производства 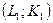и целесообразно лишь в том случае, когда .

3. Свойство делимости. Процесс производства целесообразно осуществлять в сокращенных масштабах, если выполняется следующее условие: , где 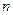- любое положительное число.

Но данное свойство не выполняется для малых предприятий.

4. Отдача от масштаба. Если затраты и 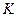изменяются в раз, то выпуск изменяется в раз:

При этом,

1) если , то имеем неизменную отдачу от масштаба;

2) если , то имеем возрастающую отдачу от масштаба;

3) если 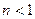, то имеем убывающую отдачу от масштаба.

В зависимости от ситуации, складывающейся на рынке, фирма то расширяет, то сокращает объем производства. В краткосрочном периоде трудно изменить объем используемых факторов производства – установить новое оборудование, расширить производственные площади и т.п. Состояние и параметры факторов производства в краткосрочном периоде определены предшествующими решениями фирмы. В долговременном периоде все факторы производства являются переменными.

Проанализируем часто встречающийся на практике случай, когда в краткосрочном периоде объем используемого капитала остается постоянным, а затраты труда изменяются. Труд является переменным фактором. Производственная функция имеет вид: 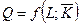, где .

Рисунок 32.

Кривые общего, среднего и предельного продукта труда

1) Построим кривую общего продукта (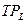) (рис. 32). В точке 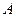выпуск растет быстрее роста затрат труда. В точке выпуск и затраты растут одинаковыми темпами. Точка 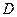демонстрирует максимально возможный выпуск.

Кривая общего продукта показывает зависимость между выпуском и затратами одного фактора.

2) Кривая предельной производительности (рис. 32). До точки предельная производительность труда () возрастает, т.к. выпуск растет быстрее затрат. В точке 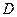, в ней дополнительное увеличение труда начинает сокращать выпуск.

3) Кривая среднего продукта труда (рис. 32). Средний продукт труда () растет до точки , затем снижается. В точке .

- средняя производительность труда (или средний продукт).

Дата добавления: 2015-10-29