Агроинженерия 5 страница

Цифра 16 получается потому, что диаметр

d^ˡ = 2 · d, .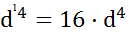

45. При испытании насоса получены следующие данные: избыточное давление на выходе из насоса =0,35МПа; вакуум перед входом в насос 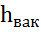=294мм рт. ст, подача Q=6,5л/с; вращающий момент на валу насоса М=41Н·м; частота вращения вала насоса n=800об/мин. Определить мощность, развиваемую насосом, потребляемую мощность и КПД насоса. Диаметры всасывающего и напорного трубопроводов считать одинаковыми.

Решение: Записываем выражение для определения КПД насоса

Η = ,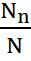

где 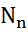-полезная мощность насоса; −потребляемая мощность.

Полезная мощность насоса определяется как произведение давления насоса на его подачу

.

Давление насоса равно разности абсолютных давлений в нагнетательном и всасывающем трубопроводах.

.

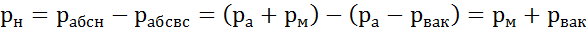Вакуумметрическое давление:

.

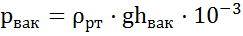Подставляя полученные выражения для , получим:

.

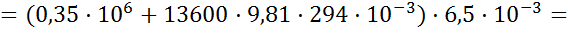
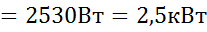Мощность потребляемая:

N = M · ω = M · =

.

КПД насоса:

η =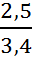

46. Центробежный насос системы охлаждения двигателя имеет рабочее колесо диаметром =200мм, с семью радиальными лопатками, диаметр окружности входа 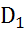=100мм. Какую частоту вращения нужно сообщить валу этого насоса при работе на воде для получения давления насоса р=0,2МПа? Гидравлический КПД насоса принять равным η_г=0,7.

Решение: Вначале запишем формулу, из которой можно выразить искомую частоту вращения вала насоса:

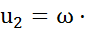
или ,

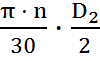откуда n = .

В правой части уравнения неизвестна окружная скорость . Необходимо написать формулу, в которую входила бы эта величина - это формула для определения теоретического напора насоса при схеме бесконечного числа лопаток:

= ).

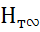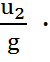
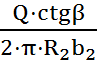Так как угол β=90, и второе слагаемое в скобках тоже равно нулю и, таким образом,

откуда .

С другой стороны, действительный напор насоса можно представить как:

Н = ,

а теоретический при схеме бесконечного числа лопаток

.

Подставляя полученные выражения для и 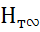в уравнение для определения n, получим

n= .

Коэффициент влияния числа лопаток определяется по формуле Пфлейдерера:

K = .

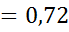здесь z=7 - число лопаток φ – коэффициент, учитывающий влияние направляющего аппарата, (принимаем φ=1). Подставив в правую часть уравнения численные значения величин, находим частоту вращения вала насоса

n = = = 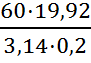1900 мин^-1.

47. Центробежный насос работает с частотой вращения 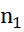=1500 об/мин и перекачивает жидкость по трубопроводу, для которого задана кривая потребного напора = (см. рис.). На том же графике дана характеристика насоса при указанной частоте вращения. Какую частоту вращения насоса нужно сообщить данному насосу, чтобы увеличить подачу жидкости в два раза?

Решение: Из графика по точке пересечения напорных характеристик насоса и трубопровода находим, что и 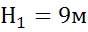. По условию задачи На графике на кривой отмечаем точку, соответствующую этой подаче и по оси напоров находим соответствующий этой подаче напор . Используя формулу пропорциональности

= ,

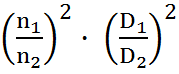при (т. к. насос один и тот же), получим

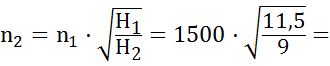1696мин^-1.

48. Номинальная частота вращения двигателя внутреннего сгорания n=4000 об/мин. Насос системы охлаждения потребляет при этом 1,5% полезной мощности. Определить долю мощности, потребляемую насосом на форсированном режиме (n=6000 об/мин) и на режиме холостого хода (n=1000 об/мин). Принять, что мощность двигателя растет пропорционально частоте вращения; характеристика системы охлаждения квадратична.

Решение: Доля мощности, потребляемая насосом на форсированном режиме,

= 2,25 .

На режиме холостого хода:

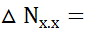
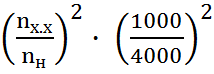= 0,0625 .

49. Центробежный насос поднимает воду на высоту h=6м по трубопроводу длиной ℓ =700м и диаметром d=150мм. Коэффициент гидравлического трения λ=0.03, суммарный, коэффициент местных сопротивлений ∑ ζ=12. Характеристика насоса при n=1000мин^-1 приведена в таблице.

Определить: 1. Подачу, напор и мощность, потребляемую насосом.

2. Подачу воды в трубопровод и напор при параллельном включении двух одинаковых насосов.

3. Подачу воды в трубопровод и напор при последовательном включении двух одинаковых насосов.

4. Как изменится подача и напор насоса при уменьшении частоты вращения до n₂=900мин^-1?

Q,л/с
Н, м		10.2	9.7	8.8	7.6	6.0
η		0.28	0.51	0.63	0.65	0.55

Решение: Эта задача решается графо-аналитическим путем. Для того чтобы выполнить первый пункт, необходимо табличные данные характеристики насоса представить в виде графика и на том же графике и в таком же масштабе построить напорную характеристику трубопровода. Точка пересечения кривых напорных характеристик насоса и трубопровода (Н_н=Н_потр) - есть режимная точка А, по которой определяется подача и напор насоса при работе на данный трубопровод.

	Q,
	Н, м		10.2	9.7	8.8	1.6	6.0
	η		0.28	0.51	0.63	0.65	0.55
	Нпотр	6.0	6.4	7.6	9.6	12.3	16.0
	Q^'
	Н^"		20.4	19.4	17.6	15.2	12.0
	Q2		3.6	7.2	10.8	14.4	18.0
	Н2	8.1	8.3	7.9	7.1	6.2	4.9

Потребный напор трубопровода складывается из геометрического 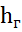и потерь напора линейных и местных.

Н_потр = h_г + · .

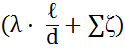Для удобства расчетов эту формулу можно представить так:

Н_потр = h_г + а · Q²,

где

а =

= .

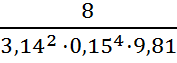
Таким образом, формула для потребного напора запишется следующим образом:

Н_потр = 6 + 0,0248 · Q²,

где Q подставляется в формулу в л/с, а его значения принимаются равными заданным в таблице исходных данных. Полученные значения Н_потр занесем в таблицу (строка 4).

В пятую строку таблицы занесем значения подач Q' для параллельно соединенных двух одинаковых насосов, при этом расходы складываются. В данном случае они удваиваются, т.е Q' =2Q.

В шестую строку заносятся значения напоров Н" для двух последовательно соединенных насосов. В этом случае напоры складываются (удваиваются), т.е. Н"=2Н.

В седьмую строку заносятся значения подач Q₂ насоса, работающего при частоте вращения n₂=900 об/мин. Значения подач Q₂ определяются по формуле пересчета:

Q₂ = Q₁· ,

Например: Q₂ = 4 · = 3,6л/с.

В восьмую строку заносятся значения напоров Н₂, определяемых по формуле пересчета:

H₂ = H₁ · ,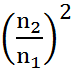

Например: Н₂ = 10 · = 8,1м.

По данным таблицы на графике в координатах Q - H строим напорные характеристики насоса, работающего при частоте вращения n₁=1000об/мин, и n₂=900об/мин, совместную напорную характеристику двух параллельно и последовательно соединенных насосов и напорную характеристику трубопровода. По точкам пересечения кривых напорных характеристик насосов и трубопровода из графика определяем напоры и подачи: N₁; Q₁ - т. А, Н' и Q'-т. А', Н" и Q"- т. А" и Q₂ и Н₂ – т. А₂.

1. Подача насоса Q₁=11,2 , напор Н₁=9.1м;

КПД насоса ;

Мощность насоса:

N = =

=

2. Подача и напор двух параллельно работающих насосов: Q' = 12,8 л/с; Н' = 10 м.

3. Подача и напор двух последовательно соединенных насосов: Q 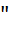= 17,8 л/с; Н" = 13,8 м.

При частоте вращения n₂ подача и напор насоса соответственно равны: Q₂ = 8,3 л/с; что при Н₂ = 7,7 м.

Из построенного графика видно, что при крутой характеристике трубопровода для увеличения подачи насосы целесообразно соединять последовательно и параллельно - при пологой.

50.Пластинчатый насос имеет следующие размеры: диаметр внутренней поверхности статора D=100мм; эксцентриситет е=10мм; толщина пластин δ=3м; ширина пластин b=40мм. Определить мощность, потребляемую насосом, при частоте вращения n=1450об/мин и давлении на выходе из насоса р=5 МПа. Механический КПД принять равным η_м=0,9.

Решение: Потребляемая насосом мощность определяется как произведение давления на подачу с учетом механического КПД:

N = .

Подача насоса зависит от его рабочего объёма и частоты вращения, т. е.

Q = V·n/60.

Рабочий объем пластинчатого насоса зависит от его конструктивных параметров и определяется по формуле

V = 2·e·(π·D - δ·z) в.

Подставляя значения рабочего объёма и подачи в исходную формулу, запишем, что

N = .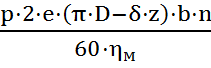

Найдём численное значение потребляемой мощности

N = =

.

51. Гидромотор развивает вращающий момент М=100Н·м при частоте вращения n=1800мин^-1. Определить расход, давление и мощность потока жидкости на входе в гидромотор, если его рабочий объем V=50см³, механический КПД η_м=0,96, объемный КПД η₀=0,95, а давление жидкости на сливе =80кПа.

Решение: Мощность на входе в гидромотор:

,

Где - мощность на выходе из гидромотора.

=

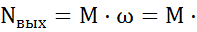
= 100 · .

Определим мощность на входе:

.

Расход потока при входе в гидромотор

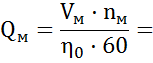
= = 1579 · 10^-6м³/с = 1,58 л/с.

Давление потока жидкости на входе в гидромотор складывается из давления в самом гидромоторе и давления на сливе:

.

Давление жидкости в гидромоторе:

.

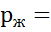
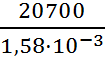
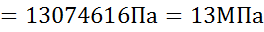52. Поршневой насос двухстороннего действия диаметром цилиндра D=280мм, ходом поршня Ɩ=200мм и диаметром штока заполняет бак вместимостью V=1,6 за 1,5мин. Определить объемный КПД насоса, если частота вращения кривошипа n=50 .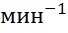

Решение: Объемный КПД представляет собой отношение фактической подачи насоса к теоретической

η₀= .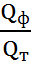

Фактическая (действительная) подача насоса:

= = 17,8л/с.

Теоретическая подача насоса определяется произведением его рабочего объема на частоту вращения

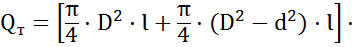
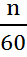
или

=

= .

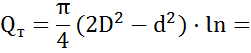
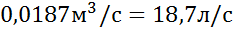Таким образом, объемный КПД насоса равен:

η = .

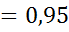53. Шестеренный насос развивает давление =6,5МПа при частоте вращения n=1200мин^-1. Определить потребляемую им мощность, если ширина шестерни b=30мм, диаметр начальной окружности =60мм, число зубьев z=8, объемный КПД η₀=0,85, КПД насоса η=0,72.

Решение: Мощность, потребляемая насосом, определяется по формуле

.

Подачу насоса выражаем через рабочий объем и частоту вращения

Q=V·n/60.

Рабочий объем шестеренного насоса:

V=2· 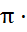D·m·b.

В приведенной формуле неизвестная величина m-модуль зацепления

m = .

Подставив полученные выражения для модуля m, рабочего объема V в исходное уравнение, найдем мощность, потребляемую насосом:

= =

=

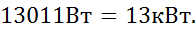
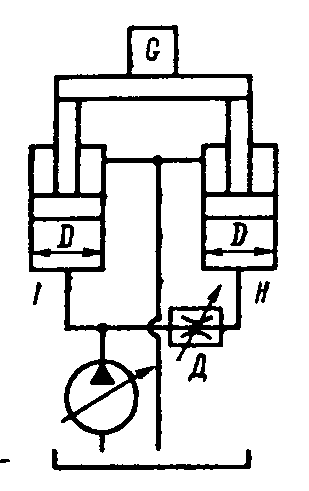54. Для подъема груза G со скоростью υ=0,15 м/с использу.тся два гидроцилиндра диаметром D=100мм. Груз смещен относительно оси cимметрии так, что нагрузка на штоке 1-го цилиндра 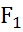=6кН, а на штоке 2-го цилиндра =5кН. Каким должен быть коэффициент местного сопротивления дросселя, чтобы платформа поднималась без перекашивания? Диаметр трубопровода d=10мм; плотность жидкости =900 кг/ . Потерями на трение по длине трубы пренебречь.

Решение: Так как груз поднимается равномерно, без перекосов платформы, то расходы жидкости в гидроцилиндрах одинаковы:

.

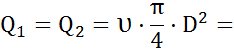
Давление, с которым жидкость приходит в гидроцилиндры, тоже должно быть одинаковым; т. е:

или △ .

Давление в гидроцилиндрах обусловлено внешними нагрузкам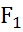и и и перепад давления на дросселе:

- = · - ).

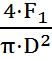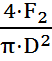С другой стороны, перепад давления на дроселе можно выразить по формуле Вейсбаха:

.

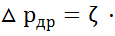
Приравняв правые части полученных выражений для 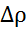полученное уравнение запишем относительно искомой величины ζ – коэффициента местного сопротивления дросселя:

· - ) и

ζ = =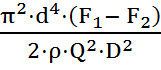

= .

55. Найти минимальные рабочие объемы гидромашин гидропередачи, обеспечивающие на выходном валу гидромотора момент М=50Н·м и угловую скорость =200с^-1, если угловая скорость насоса 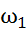=300с^-1, давление срабатывания предохранительного клапана . Принять объёмные КПД гидромашин η₀=0,95; механические КПД η_м=0,92. Какую мощность при этом потребляет насос?

Решение: По известным данным определим мощность, потребляемую гидромотором:

.

Рабочий объем гидромотора найдем из формулы мощности:

,

Дата добавления: 2015-10-29