Исследование формы и спектра сложных гармонических сигналов.

Государственное образовательное учреждение высшего профессионального образования

Ульяновский государственный университет.

Факультет Математики и информационных технологий

Кафедра Телекоммуникационных технологий и сетей.

Лабораторная работа №2

по дисциплине:

«Основы передачи дискретных данных»

Тема:

«Исследование спектров сигналов»

Выполнили:

Вислов К.

Звягинцева Е.

Никонов Н.

Косян П.

Козлов Д.

Дуницына С.

Камалтдинов Д.

Крапивцев И.

Минеев Е.

Студенты гр. ИС-О-09/1

Ульяновск 2012г.

Цель работы

Исследование формы и спектра гармонических сигналов и периодических последовательностей импульсов. Формирование навыков спектрального анализа сигналов на ПК.

Задание.

1. Исследовать форму и спектры простейших гармонических сигналов.

2. Исследовать форму и спектры сложных гармонических сигналов.

3. Исследовать связь формы и спектра периодических последовательностей
прямоугольных импульсов.

Исследование формы и спектра простых гармонических сигналов.

В качестве простейшего гармонического сигнала для исследования будем использовать сигнал с частотой 1 кГц. Осциллограмма этого сигнала показана на рис.1.

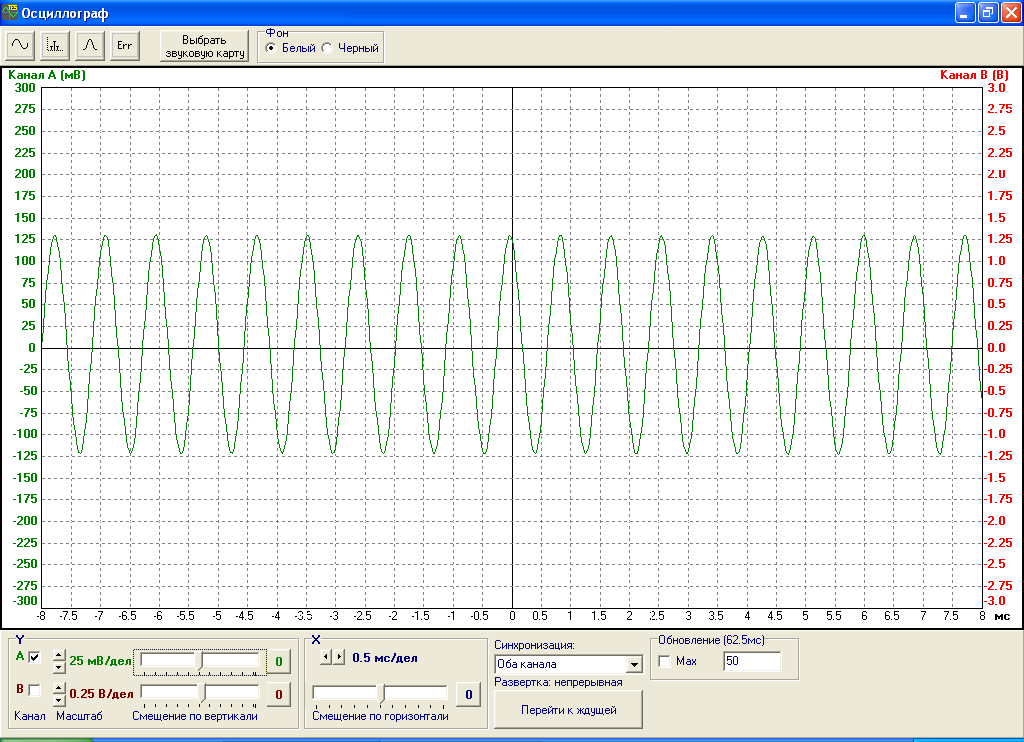
Рис.1. Осциллограмма гармонического сигнала с частотой 1 кГц.

По рис.1. определим период и амплитуду исследуемого сигнала. Для данного сигнала период T равен 0,85 мс, амплитуда составляет 125 мВ.

Известно, что любой периодический сигнал x(t) можно представить в виде суммы гармонических колебаний с частотами, кратными основной частоте f=1/T, и с некоторыми амплитудами. Совокупность таких амплитуд образует амплитудный спектр сигнала. Линейчатый амплитудный спектр исследуемого периодического сигнала изображен на рис.2.

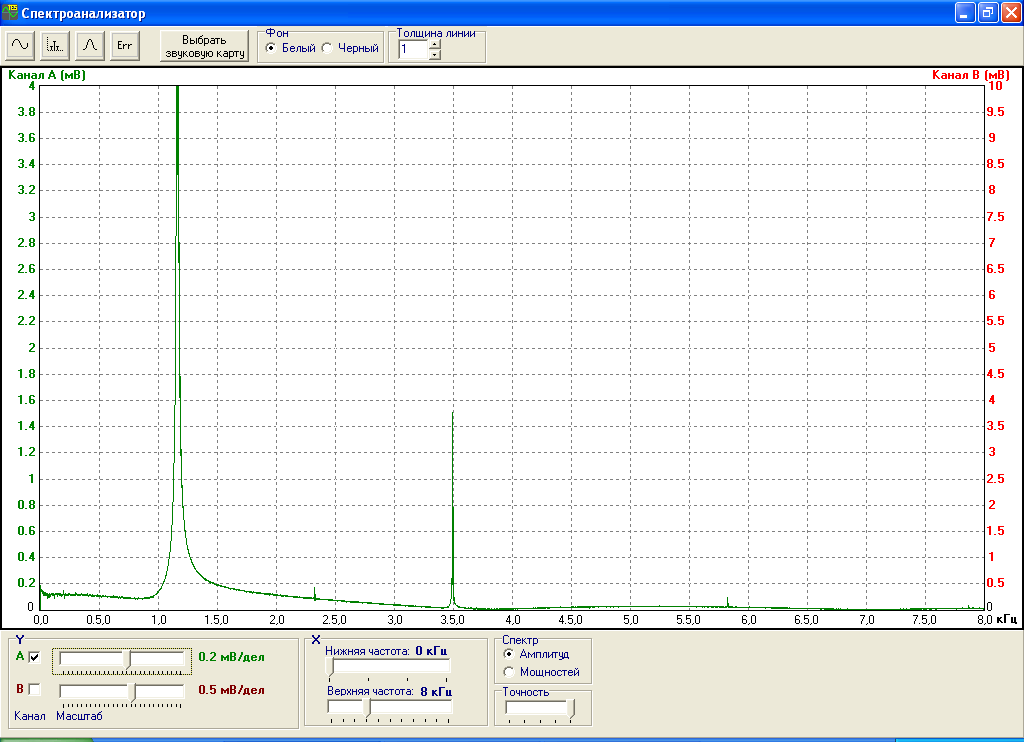
Рис.2. Линейчатый амплитудный спектр сигнала с частотой 1 кГц.

Исходя из выражения f=1/T, основная гармоника сигнала имеет частоту 1/0.85 = 1.17 кГц и амплитуду 4.4 мВ, что отражено на рис.2. Также можно сделать вывод, что сигнал состоит из еще одной гармоники с частотой 3f=3.51 кГц и амплитудой 1.5 мВ.

Исследование формы и спектра сложных гармонических сигналов.

Теперь исследуем спектр сложных сигналов. На вход осциллографа подадим сигнал s1(t), который состоит из двух гармоник 2 кГц и 4 кГц. Осциллограмма этого сигнала изображена на рис.3.

Рис.3. Осциллограмма сигнала s1(t).

Согласно рис.3, период сигнала составляет 0.42 мс. Соответственно, частота сигнала f равна 1/0.42 = 2.38 кГц. Спектр сигнала s1(t) показан на рис.4.

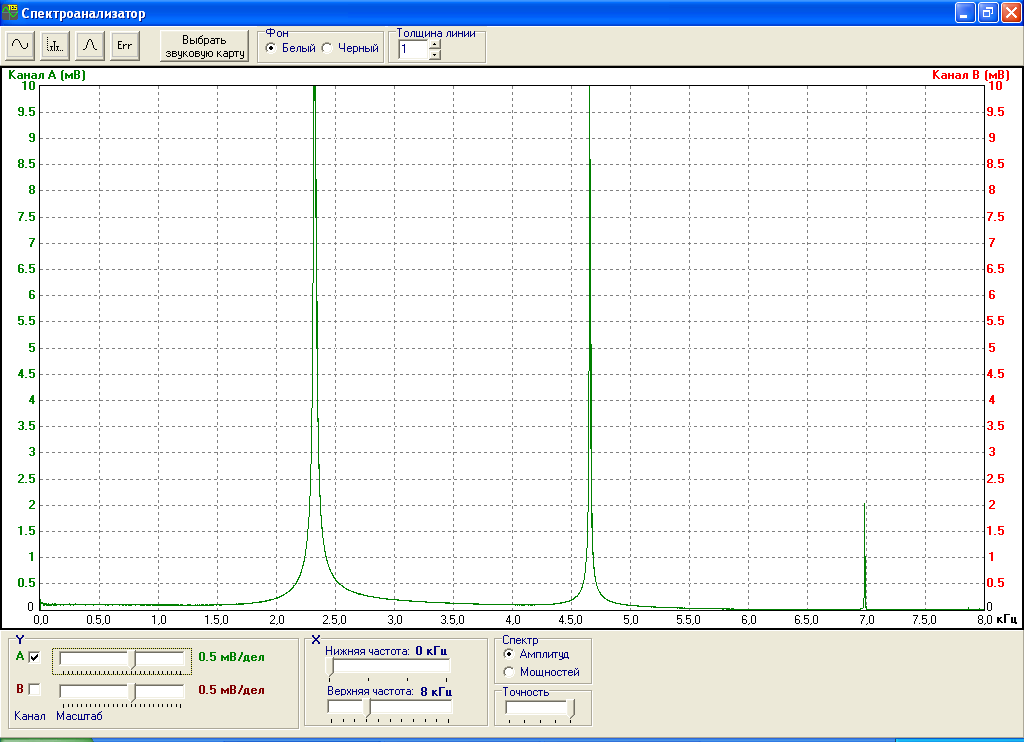
Рис.4. Спектр сигнала s1(t).

Как было сказано выше, частота сигнала составляет 2.38 кГц. Она совпадает с частотой основной гармоники. Из рис.4 видно, что сигнал s1(t) состоит из гармоник с частотами f=2.38 кГц, 2f=4.76 кГц и 3f=7.14 кГц. Их амплитуды соответственно равны 12, 10.2 и 2 мВ.

Далее рассмотрим спектры сигналов s2(t) и s3(t), состоящих из гармоник 2 кГц и 6 кГц. Сигналы s2(t) и s3(t) отличаются только фазой третьей гармоники.

Осциллограмма сигнала s2(t) показана на рис.5.

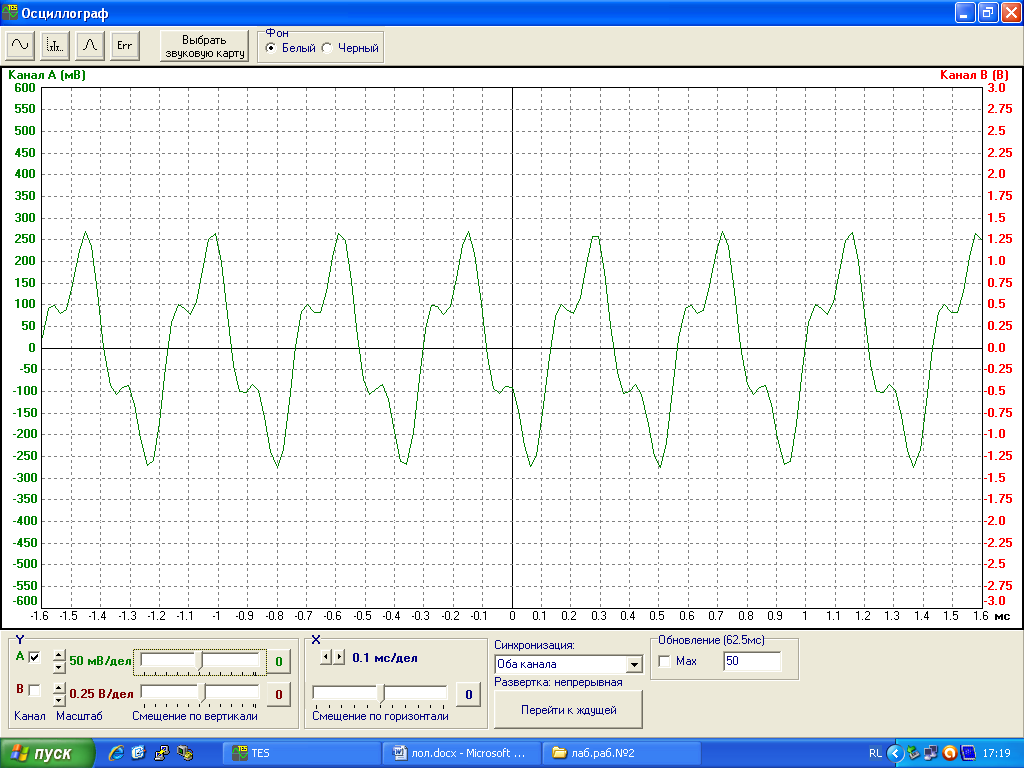
Рис.5. Осциллограмма сигнала s2(t).

Период сигнала s2(t) такой же, как и у сигнала s1(t) – 0.42 мс (см. рис. 3). Соответственно, f = 1/0.42 = 2.38 кГц. Спектр сигнала s2(t) изображен на рис.6.

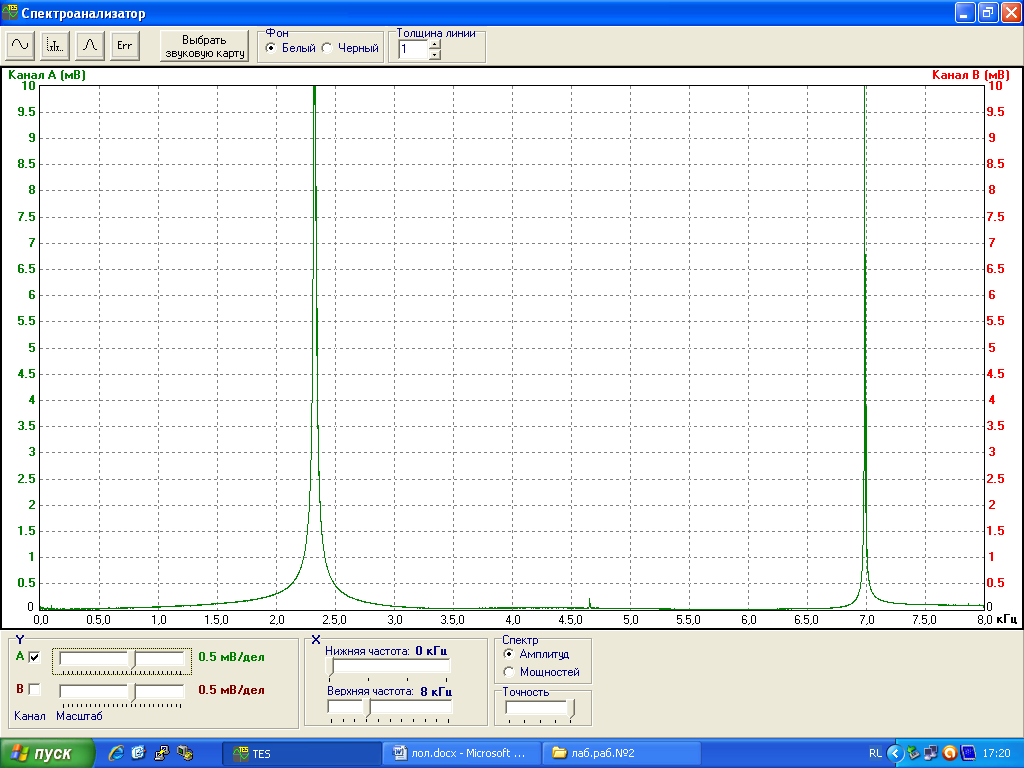
Рис.6. Спектр сигнала s2(t).

Исходя из рис.6, сигнал состоит из двух гармоник с частотами f=2.38 кГц и 3f=7.14 кГц соответственно. Их амплитуды соответственно равны 12 и 10.2 мВ.

Теперь рассмотрим сигнал s3(t). Его осциллограмма и спектр изображены на рис.7. и на рис.8.

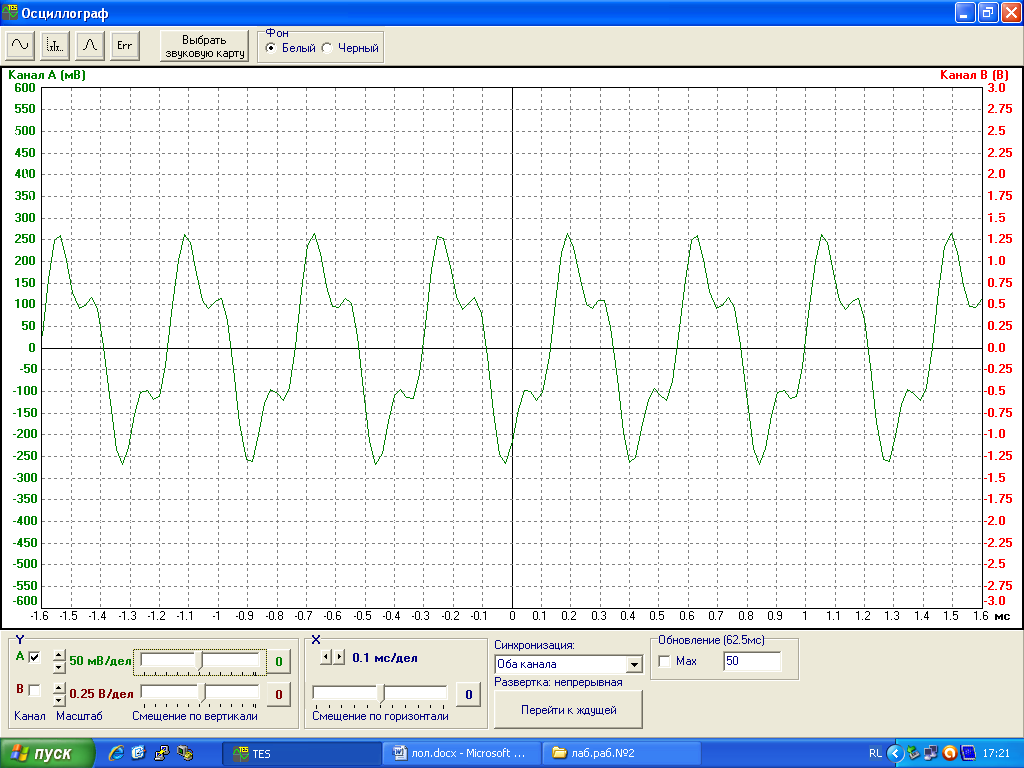
Рис.7. Осциллограмма сигнала s3(t).

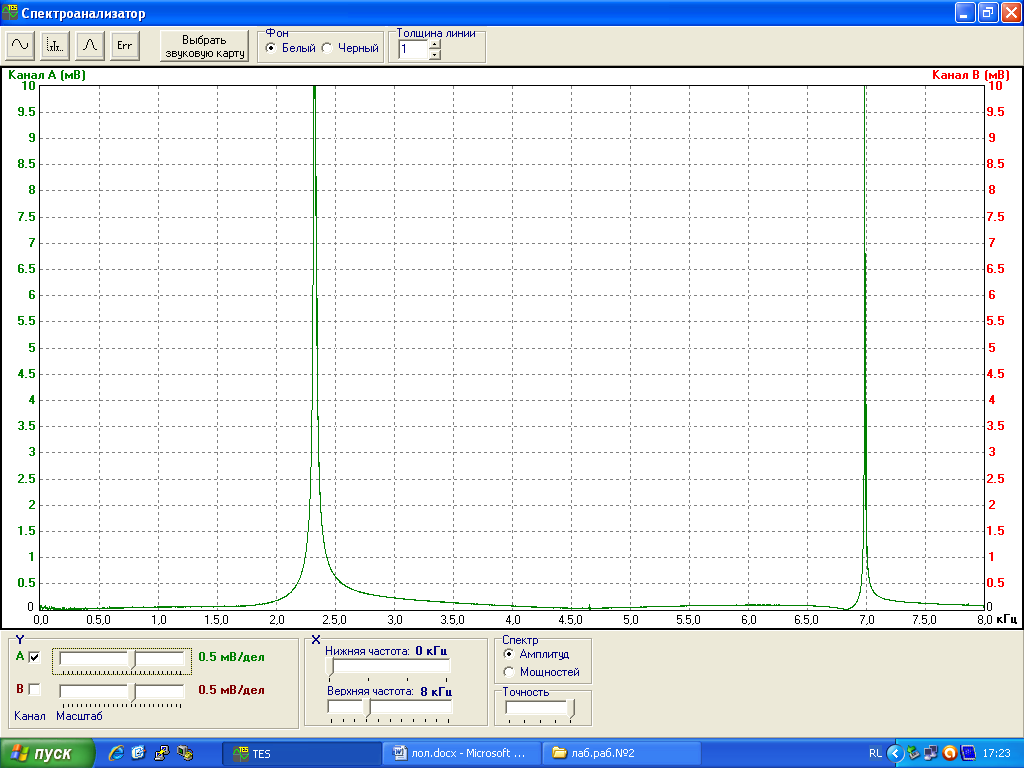
Рис.8. Спектр сигнала s3(t).

Поскольку сигналы s2(t) и s3(t) отличаются между собой только фазой третьей гармоники, то их периоды равны между собой (см. рис.5 и рис. 7). Спектры указанных сигналов также совпадают, т.к. изменение фазы колебания не влияет на изменение частоты колебания – гармоники, составляющие сигнал s3(t) остались такими же по сравнению с гармониками сигнала s2(t) (см. рис.6 и рис.8).

Далее выясним, как получается спектр суммы двух сигналов. Для этого на первый вход сумматора подадим сигнал s2(t), а на второй – сигнал с частотой 1 кГц. Напомним, что спектр каждого сигнала в отдельности уже получен (см. рис.2 и рис.5). Зафиксируем осциллограмму с выхода сумматора. Полученная осциллограмма изображена на рис.9.

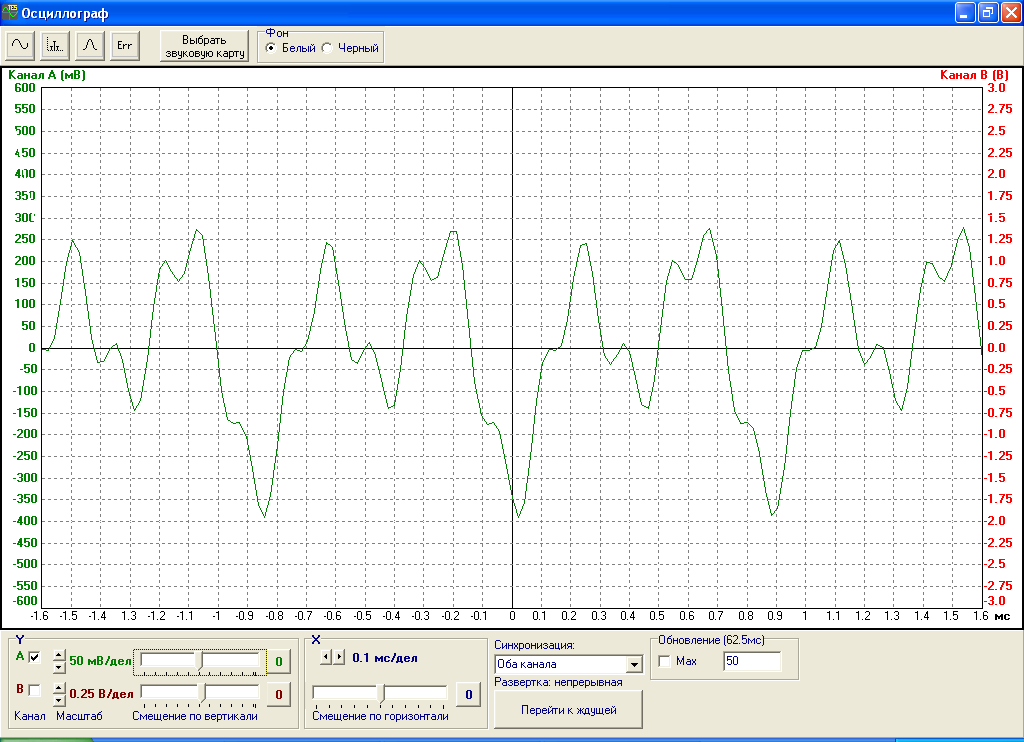
Рис.9. Осциллограмма с выхода сумматора (s2(t)+”1 кГц”).

Период данного сигнала составляет 0.85 мс и равен максимальному из периодов сигнала s2(t) (его период составляет 0.42 мс) и сигнала с частотой 1 кГц (T=0.85мс). Соответственно, основная гармоника будет иметь частоту 1/T = 1.17 кГц. Спектр исследуемого сигнала представлен на рис.10.

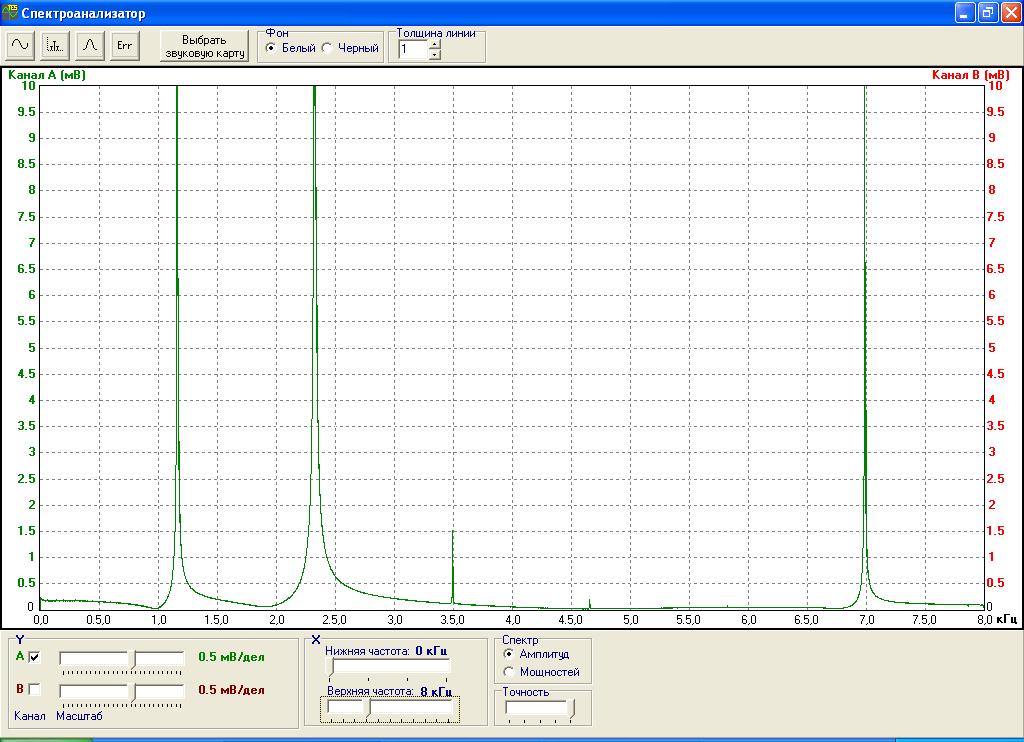
Рис.10. Спектр сигнала с сумматора (s2(t) + “1 кГц”).

Сравнивая рис.2, рис.5 и рис.10 можно сделать вывод, что спектр суммы сигналов равен сумме спектров каждого сигнала в отдельности. Для данного сигнала имеем частоты 1.17, 2.38, 3.51 и 7.14 кГц и соответствующие амплитуды в 12,11, 1.5 и 10.2 мВ.

В заключение пункта исследования сложных сигналов рассмотрим бигармонический сигнал, состоящий из сигналов с частотами 1 кГц и 1.2 кГц. Осциллограмма суммы данных сигналов показана на рис.11.

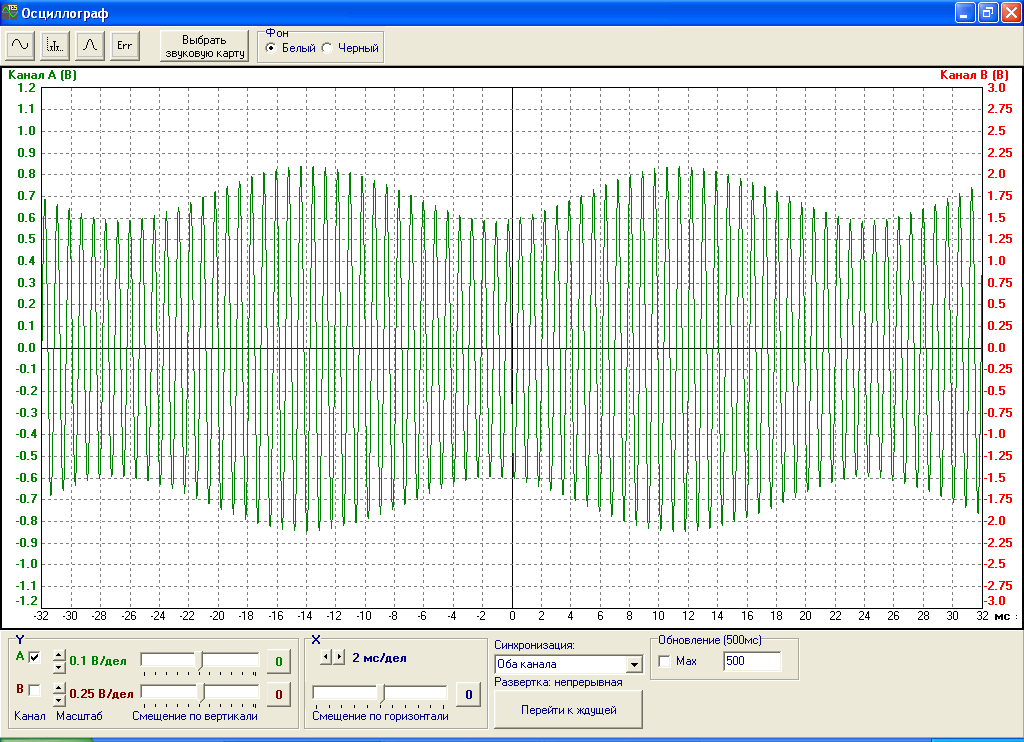
Рис.11. Осциллограмма бигармонического сигнала (1 кГц + 1.2 кГц).

Период данного сигнала равен 25.2 мс. Спектр сигнала изображен на рис.12 и равен сумме спектров каждого сигнала в отдельности.

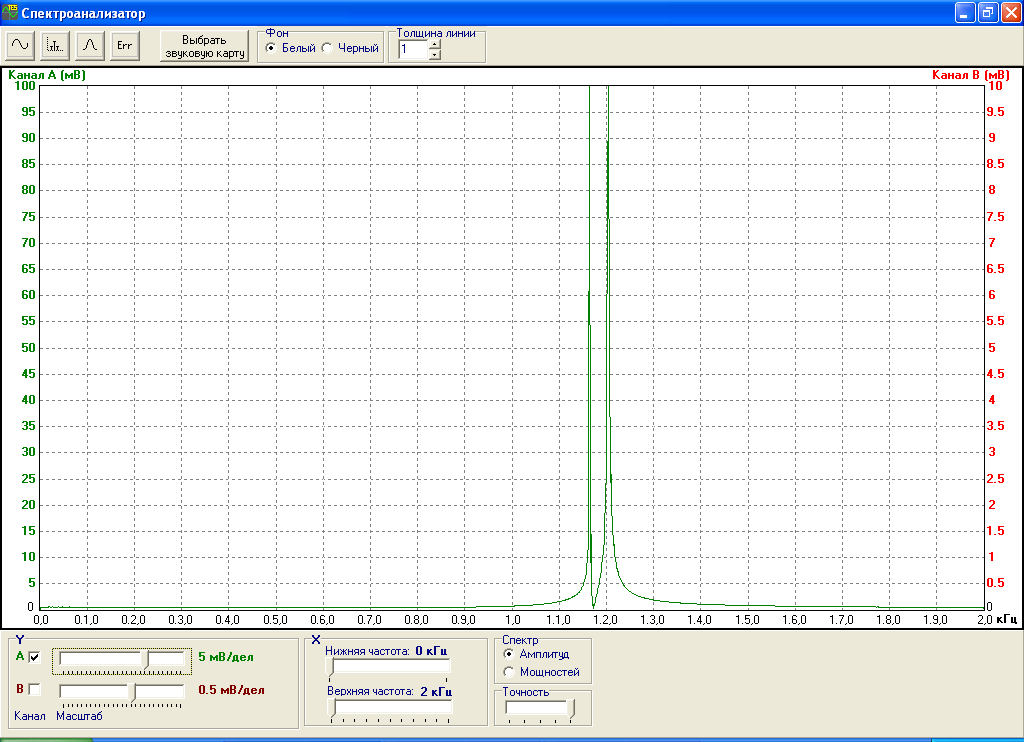
Рис.12. Спектр суммы двух сигналов с частотами 1 кГц и 1.2 кГц.

По рис.12 видим, что сигнал состоит из двух гармонических сигналов с некратными частотами 1.17 кГц (см. рис.2) и 1.21 кГц.

Дата добавления: 2015-10-29