
Читайте также:
|
Лабораторная работа №3
Транспортная задача
Вариант №1
Задача:
Для строительства 4 объектов используется кирпич изготовленный на трех заводах. Ежедневно каждый из заводов может изготовить 100, 150 и 50 усл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящхся объектов соответственно равны 70, 80, 60, 85. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого из заводов к каждому из объектов.

Составить план перевозок с минимальной стоимостью.
План выполнения работы:
1) Составить математическую модель задачи.
2) Построить первоначальный опорный план методом «северо-западного угла».
3) Найти оптимальное решение задачи методом потенциалов.
4) Оформить отчет о работе, содержащий постановку решения задачи, распечатку результатов работы программы и ответы на контрольные вопросы.
Контрольные вопросы:
1. Какие модели ТЗ называются замкнутыми, какие - открытыми?
2. Способы построения начального опорного плана.
3. Методы решения ТЗ, сущность метода потенциалов.
4. Критерий оптимальности плана перевозок согласно методу потенциалов.
5. Решение открытых ТЗ.
6. Метод решения ТЗ при запрещении некоторых перевозок.
7. ТЗ с ограничениями на пропускные способности, методы решения.
Решение:
Условие баланса:
100+150+50 = 300
70+80+60+85 = 295
Условие баланса не выполняется, в избытке запасы, вводим фиктивный пункт потребления с потребностями 300-295= 5 единиц.
Строим первоначальный опорный план методом «северо-западного угла»:
Табл.1

| 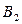
| 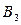
| 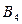
| 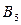
| запасы | ||

| 
| ||||||

| 
| ||||||
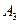
| 
| ||||||
| потребности | |||||||

| 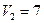
| 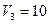
| 
| 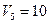
|
m+n-1=7 (условие выполняется)
Потенциалы занятых клеток: 
1) 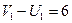

2) 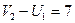

3) 

4) 
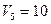
5) 

6) 

7) 
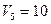
Свободные клетки: 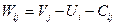
 10-0-3=7
10-0-3=7
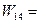 11-0-5=6
11-0-5=6
 10-0-0=10
10-0-0=10
 6-5-1=0
6-5-1=0
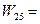 10-5-0=5
10-5-0=5
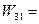 6-10-8=-12
6-10-8=-12
 7-10-10=-13
7-10-10=-13
 10-10-20=-20
10-10-20=-20
В клетку (1;5) ставим (*) и строим цикл:
Табл.2

| 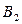
| 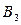
| 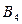
| 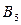
| запасы | ||

| 
| ||||||

| 
| ||||||
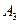
| 
| ||||||
| потребности | |||||||

| 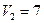
| 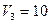
| 
| 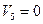
|
Свободные клетки: 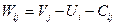
 10-0-3=7
10-0-3=7
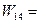 11-0-5=6
11-0-5=6
 6-5-1=0
6-5-1=0
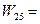 0-5-0=-5
0-5-0=-5
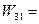 6-10-8=-12
6-10-8=-12
 7-10-10=-13
7-10-10=-13
 10-10-20=-20
10-10-20=-20
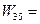 0-10-0=-10
0-10-0=-10
В клетку (1;3) ставим (*) и строим цикл:
Табл.3

| 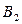
| 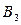
| 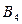
| 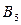
| запасы | ||

| 
| ||||||

| 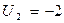
| ||||||
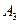
| 
| ||||||
| потребности | |||||||

| 
| 
| 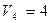
| 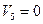
|
Свободные клетки: 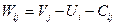
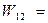 0-0-7=-7
0-0-7=-7
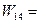 4-0-5=-1
4-0-5=-1
 6+2-1=7
6+2-1=7
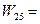 0+2-0=2
0+2-0=2
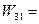 6-3-8=-5
6-3-8=-5
 0-3-10=-13
0-3-10=-13
 3-3-20=-20
3-3-20=-20
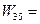 0-3-0=-3
0-3-0=-3
В клетку (1;2) ставим (*) и строим цикл:
Табл.4

| 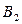
| 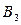
| 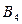
| 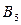
| запасы | ||

| 
| ||||||

| 
| ||||||
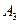
| 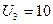
| ||||||
| потребности | |||||||

| 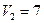
| 
| 
| 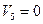
|
Свободные клетки: 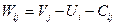
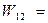 7-0-7=0
7-0-7=0
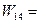 11-0-5=6
11-0-5=6
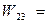 3-5-5=-7
3-5-5=-7
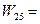 0-5-0=-5
0-5-0=-5
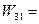 6-10-8=-12
6-10-8=-12
 7-10-10=-13
7-10-10=-13
 3-10-20=-27
3-10-20=-27
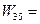 0-10-0=-10
0-10-0=-10
В клетку (1;4) ставим (*) и строим цикл:
Табл.5

| 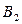
| 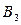
| 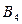
| 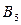
| запасы | ||

| 
| ||||||

| 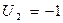
| ||||||
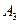
| 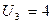
| ||||||
| потребности | |||||||

| 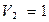
| 
| 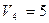
| 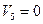
|
Свободные клетки: 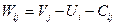
 0-0-6=-6
0-0-6=-6
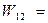 1-0-7=-6
1-0-7=-6
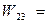 3+1-5=-1
3+1-5=-1
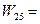 0+1-0=1
0+1-0=1
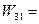 0-4-8=-12
0-4-8=-12
 1-4-10=-13
1-4-10=-13
 3-4-20=-21
3-4-20=-21
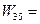 0-4-0=-4
0-4-0=-4
В клетку (2;5) ставим (*) и строим цикл:
Табл.6

| 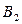
| 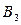
| 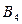
| 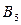
| запасы | ||

| 
| ||||||

| 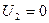
| ||||||
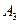
| 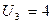
| ||||||
| потребности | |||||||

| 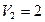
| 
| 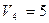
| 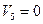
|
Свободные клетки: 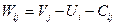
 1-0-6=-5
1-0-6=-5
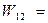 2-0-7=-5
2-0-7=-5
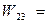 3-0-5=-2
3-0-5=-2
 5-0-6=-1
5-0-6=-1
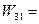 1-4-8=-11
1-4-8=-11
 2-4-10=-12
2-4-10=-12
 3-4-20=-21
3-4-20=-21
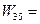 0-4-0=-4
0-4-0=-4
Положительных нет, следовательно план является оптимальным.
Проверяем стоимость перевозки:
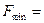 60*3+35*5+70*1+80*2+50*1=180+175+70+160+50=635
60*3+35*5+70*1+80*2+50*1=180+175+70+160+50=635
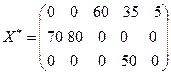
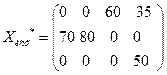
Ответы на контрольные вопросы
1. Какие модели транспортных задач называются замкнутыми, какие – открытыми?
Транспортная задача также относится к задачам линейного программирования. Она состоит в наиболее рациональном закреплении пунктов отправления некоторого однородного продукта к пунктам потребления, при этом в качестве критерия оптимальности берется либо минимальная стоимость перевозок, либо минимальное время доставки груза.
Важность этих задач и специфика получающихся ограничений позволили разработать более эффективный по сравнению с симплекс-методом алгоритм решений.
Математическая модель задачи:
Обозначим пункты отправления  . В каждом из этих пунктов запасы груза —
. В каждом из этих пунктов запасы груза —  . Пункты назначения обозначаются
. Пункты назначения обозначаются 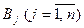 и потребности каждого
и потребности каждого 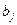 . Выполняется условие баланса. Задана матрица стоимостей
. Выполняется условие баланса. Задана матрица стоимостей 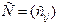 :
:
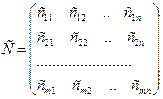
Требуется найти матрицу транспортных перевозок  , которая бы обеспечила минимум стоимости перевозок.
, которая бы обеспечила минимум стоимости перевозок.
Составим целевую функцию:

Запишем ограничения:
1) Все грузы должны быть вывезены

2) Все потребности должны быть удовлетворены

3) Грузы перевозятся из пунктов отправления в пункт назначения:

4) Выполняется условие баланса:

Если последнее условие не выполняется, то задача называется открытой.
Если условия (1)-(5) выполняются, то имеем закрытую ТЗ.
Способы построения начального опорного плана.
Существует два способа поиска начального опорного плана:
1) метод северо-западного угла;
2) метод минимальных затрат.
Сущность этих методов состоит в том, что опорный план находится последовательно за (m+n-1) шагов. На каждом шаге в таблице условий задачи заполняется одна клетка, которую называют занятой. Заполнение одной из клеток позволяет либо удовлетворить потребности в грузе одного из пунктов назначения, либо вывести все грузы из какого-то пункта отправления.
В первом случае временно исключают из рассмотрения столбец, содержащий заполненную клетку, и рассматривают задачу с таблицей условий на один столбец меньше (количество строк старое, но меняются запасы грузов).
Во втором случае временно исключают из рассмотрения строчку, содержащую заполненную клетку. Количество столбцов сохраняется, изменяются потребности в грузе.
Если на некотором шаге (но не на последнем) окажется, что потребности очередного пункта назначения равны запасам очередного пункта отправления, то исключают из рассмотрения либо строчку, либо столбец (но только одно!) и либо запасы соответствующего пункта отправления, либо потребности в грузе данного пункта назначения считают равными 0. Этот нуль записывают в очередную заполняемую клетку и ее считают занятой. Это гарантирует получение (m+n-1) занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием проверки опорного плана на оптимальность.
В методе северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления новый из оставшихся пунктов назначения. Заполнение таблицы начинают с 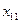 и заканчивают
и заканчивают  .
.
В методе минимальных затрат на каждом шаге выбирается клетка с минимальным тарифом. Этот метод позволяет найти опорный план ТЗ, при котором стоимость перевозок меньше, чем в методе северо-западного угла.
Методы решения ТЗ. Сущность метода потенциалов.
Для определения оптимального плана используют метод потенциалов.
Теорема.
Если для некоторого опорного плана  в транспортной задаче существуют такие числа
в транспортной задаче существуют такие числа  ,
,  ,..,
,..,  и
и 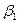 ,
, 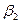 ,..,
,..,  , для которых выполняются условия
, для которых выполняются условия
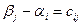 (
( ) (6)
) (6)
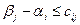 (
(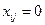 ) (7)
) (7)
для всех 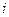 и
и 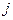 , то
, то  — оптимальный план.
— оптимальный план.
Пусть найден некоторый опорный план. Для каждого пункта отправления и назначения определяют потенциалы 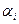 ,
, 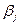 из соотношения (6). Так как число неизвестных на единицу больше числа заполненных клеток, то одно из
из соотношения (6). Так как число неизвестных на единицу больше числа заполненных клеток, то одно из 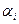 берут равным 0 (чаще всего
берут равным 0 (чаще всего 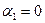 ), и находят все остальные
), и находят все остальные 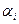 и
и 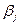 . После того, как все потенциалы найдены, для каждой из свободных клеток вычисляют
. После того, как все потенциалы найдены, для каждой из свободных клеток вычисляют 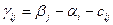 .
.
Если среди 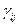 нет положительных, то опорный план — оптимальный.
нет положительных, то опорный план — оптимальный.
Если для некоторой свободной клетки 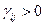 , то полученный опорный план неоптимальный и необходимо сделать пересчет таблицы. Для этого рассматривают все свободные клетки, для которых
, то полученный опорный план неоптимальный и необходимо сделать пересчет таблицы. Для этого рассматривают все свободные клетки, для которых 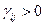 . Из этих чисел выбирают максимальное. Клетку, которой соответствует максимальное число, необходимо заполнить, изменив объемы поставок, связанных с выбранной клеткой так называемым циклом.
. Из этих чисел выбирают максимальное. Клетку, которой соответствует максимальное число, необходимо заполнить, изменив объемы поставок, связанных с выбранной клеткой так называемым циклом.
Циклом называется ломаная, вершины которой находятся в занятых клетках таблицы, а звенья параллельны строкам и столбцам, причем в каждой вершине цикла встречается ровно 2 звена.

 Если ломаная, образующая цикл, пересекается, то точки самопересечения не являются вершинами.
Если ломаная, образующая цикл, пересекается, то точки самопересечения не являются вершинами.
 |
При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл.
После того, как для выбранной клетки построили цикл, следует перейти к любому опорному плану, т.е. переместить грузы в пределах клеток, связанных с выбранной свободной клеткой циклом по следующим правилам:
1) каждой из клеток цикла приписывают знак, причем выбранной свободной клетке “+”, а всем остальным “-”, “+” и т.д.
2) в данную свободную клетку переносят меньшую из чисел 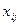 , стоящих в минусовых клетках. Одновременно это число прибавляется к соответствующим числам в клетках с “+” и вычитается в клетках с “-”.
, стоящих в минусовых клетках. Одновременно это число прибавляется к соответствующим числам в клетках с “+” и вычитается в клетках с “-”.
Клетка, которая была свободной, становится занятой, а клетка с “-”, в которой стояло минимальное из чисел 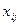 считается свободной.
считается свободной.
В результате этих перемещений грузов определяется новый опорный план ТЗ. Переход от одного плана к другому называется сдвигом по циклу пересчета.
Новый опорный план проверяется на оптимальность (методом потенциалов).
Далее все повторяется, если план не оптимальный.
При определении опорного плана или в процессе решения задачи может быть получен вырожденный опорный план. Чтобы избежать здесь зацикливания, следует соответствующие нулевые элементы опорного плана заменить на сколь угодно малое положительное  . В оптимальном плане такой задачи считаем
. В оптимальном плане такой задачи считаем 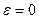 .
.
Критерий оптимальности планов перевозок согласно методу потенциалов.
Если среди 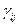 нет положительных, то опорный план — оптимальный.
нет положительных, то опорный план — оптимальный.
Дата добавления: 2015-10-29; просмотров: 365 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Готовность к аварийным ситуациям и реагирование | | | Забезпечуюча частина ІС обліку, її склад та характеристика складових. |